dB: Wat is een decibel?

Geluidsdruk, geluidsniveau en dB. Geluid wordt meestal gemeten met microfoons en die reageren evenredig met de geluidsdruk, p. Welnu, het vermogen in een geluidsgolf is, voor het overige gelijk, kwadratisch met de druk. (Op dezelfde manier is het elektrisch vermogen in een weerstand het kwadraat van de spanning). De log van x2 is gewoon 2 log x, dus dit introduceert een factor 2 wanneer we drukverhoudingen omrekenen naar decibels. Het verschil in geluidsdruk tussen twee geluiden met p1 en p2 is dus:

20 log (p2/p1) dB = 10 log (p22/p12) dB = 10 log (P2/P1) dB (overal is de log op basis 10).

Wat gebeurt er als je het geluidsvermogen halveert? De log van 2 is 0,3010, dus de log van 1/2 is -0,3, tot een goede benadering. Dus, als je het vermogen halveert, verminder je het vermogen en het geluidsniveau met 3 dB. Halveer nogmaals (tot 1/4 van het oorspronkelijke vermogen) en je vermindert het niveau met nog eens 3 dB. Als je het vermogen blijft halveren, heb je deze verhoudingen.

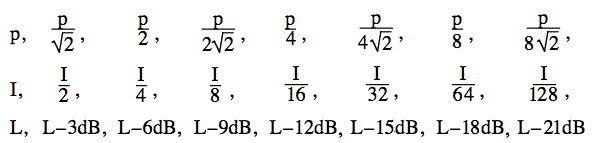
Wat gebeurt er als ik twee identieke geluiden toevoeg? Verdubbel ik de intensiteit (toename van 3 dB)? Of verdubbel ik de druk (toename van 6 dB)? Deze veelgestelde vraag is een beetje subtiel, daarom wordt hij hier in onze FAQ besproken.

Geluidsbestanden om de grootte van een decibel te laten zien

We zagen hierboven dat halvering van het vermogen de geluidsdruk met √2 en het geluidsniveau met 3 dB doet afnemen. Dat is wat we hebben gedaan in de eerste grafiek en het geluidsbestand hieronder.

Het eerste geluidsvoorbeeld is witte ruis (een mix van een breed scala aan hoorbare frequenties, analoog aan wit licht, dat een mix is van alle zichtbare frequenties). Het tweede geluid is dezelfde ruis, maar met een factor √2 verminderd. Nu is 1/√2 ongeveer 0,7, zodat -3 dB overeenkomt met een vermindering van de spanning of de druk tot 70% van de oorspronkelijke waarde. De groene lijn toont de spanning als functie van de tijd. De rode lijn toont een continu exponentieel verval met de tijd. Merk op dat de spanning met 50% daalt voor elk tweede monster. Merk ook op dat een verdubbeling van het vermogen geen groot verschil maakt voor de luidheid. We zullen dit hieronder verder bespreken, maar het is nuttig om te onthouden bij de keuze van geluidsweergaveapparatuur. Geluidsbestanden en animatie door John Tann en George Hatsidimitris.

Hoe groot is een decibel? In de volgende reeks worden de opeenvolgende samples met slechts één decibel verminderd.

Een decibel is van dezelfde orde als het Just Noticeable Difference (JND) voor het geluidsniveau. Als u naar deze bestanden luistert, zult u merken dat de laatste stiller is dan de eerste, maar het is voor het oor iets minder duidelijk dat de tweede van een paar stiller is dan zijn voorganger. 10*log10(1,26) = 1, dus om het geluidsniveau met 1 dB te verhogen, moet het vermogen met 26% worden verhoogd, of de spanning met 12%.

Wat als het verschil minder dan een decibel is? Geluidsniveaus worden zelden met decimalen aangegeven. De reden hiervoor is dat geluidsniveaus die minder dan 1 dB verschillen moeilijk van elkaar te onderscheiden zijn, zoals het volgende voorbeeld laat zien.(Dit maakt de dB een handige maateenheid.)

0,3 dB-stappen. U kunt merken dat de laatste stiller is dan de eerste, maar het is moeilijk om het verschil tussen opeenvolgende paren op te merken. 10*log10(1,07) = 0,3, dus om het geluidsniveau met 0,3 dB te verhogen, moet het vermogen met 7% worden verhoogd, of de spanning met 3,5%.

Standaard referentieniveaus (‘absoluut’ geluidsniveau)

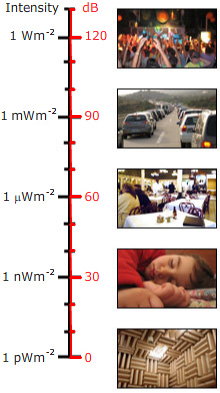We zeiden hierboven dat de decibel een verhouding is. Wanneer het wordt gebruikt om het geluidsniveau voor een enkel geluid aan te geven in plaats van een verhouding, moet dus een referentieniveau worden gekozen. Voor het geluidsdrukniveau wordt als referentieniveau (voor lucht) meestal pref = 20 micropascal (20 μPa), of 0,02 mPa gekozen. Dit is zeer laag: het is 2 tienmiljardste deel van een atmosfeer. Toch is dit ongeveer de grens van de gevoeligheid van het menselijk oor, in zijn gevoelige frequentiegebied. (Gewoonlijk wordt deze gevoeligheid alleen aangetroffen bij vrij jonge mensen of bij mensen die niet zijn blootgesteld aan luide muziek of andere harde geluiden. Persoonlijke muzieksystemen met luidsprekers in het oor zijn in staat zeer hoge geluidsniveaus in het oor te produceren, en worden door sommigen verantwoordelijk geacht voor een groot deel van het gehoorverlies bij jonge volwassenen in sommige landen).

Als u dus leest over een geluidsdrukniveau van 86 dB, betekent dit dat

20 log (p2/pref) = 86 dB

waarbij pref de geluidsdruk van het referentieniveau is, en p2 die van het geluid in kwestie. Deel beide zijden door 20:

log (p2/pref) = 4,3

p2/pref = 104,3

4 is de log van 10 duizend, 0,3 is de log van 2, dus dit geluid heeft een geluidsdruk die 20 duizend maal zo hoog is als die van het referentieniveau (p2/pref = 20.000) of een intensiteit die 400 miljoen maal zo hoog is als de referentie-intensiteit. 86 dB is een hard geluid, maar niet gevaarlijk, op voorwaarde dat de blootstelling kort is.

Wat betekent 0 dB? Dit niveau treedt op wanneer de gemeten intensiteit gelijk is aan het referentieniveau, d.w.z. het geluidsniveau dat overeenkomt met 0,02 mPa. In dit geval hebben we

geluidsniveau = 20 log (pgemeten/pref) = 20 log 1 = 0 dB

Bedenk dat decibels een verhouding meten. 0 dB ontstaat wanneer je de log neemt van een verhouding van 1 (log 1 = 0). Dus 0 dB betekent niet dat er geen geluid is, maar een geluidsniveau waarbij de geluidsdruk gelijk is aan die van het referentieniveau. Dit is een kleine druk, maar niet nul. Het is ook mogelijk om negatieve geluidsniveaus te hebben: – 20 dB zou een geluid betekenen met een druk die 10 keer kleiner is dan de referentiedruk, d.w.z. 2 μPa.

Niet alle geluidsdrukken zijn even luid. Dat komt omdat het menselijk oor niet op alle frequenties even sterk reageert: wij zijn veel gevoeliger voor geluiden in het frequentiegebied van ongeveer 1 kHz tot 7 kHz (1000 tot 7000 trillingen per seconde) dan voor zeer laag- of hoogfrequente geluiden. Daarom worden geluidsmeters meestal uitgerust met een filter waarvan de respons op de frequentie een beetje lijkt op die van het menselijk oor. (Meer over deze filters hieronder.) Als het “A wegingsfilter” wordt gebruikt, wordt het geluidsdrukniveau aangegeven in eenheden van dB(A) of dBA. Het geluidsdrukniveau op de dBA-schaal is gemakkelijk te meten en wordt daarom veel gebruikt. Een van de redenen waarom het verschilt van luidheid is dat het filter niet op dezelfde manier reageert als het oor. Om de luidheid van een geluid te begrijpen, moet u eerst enkele krommen raadplegen die de frequentierespons van het menselijk oor weergeven, hieronder weergegeven. (Een andere reden is dat het menselijk gehoor niet logaritmisch is.

Logaritmische maten

Waarom gebruiken we decibels? Het oor is in staat een zeer groot bereik aan geluiden te horen: de verhouding tussen de geluidsdruk die bij korte blootstelling blijvende schade veroorzaakt en de grens die (onbeschadigde) oren kunnen horen is meer dan een miljoen. Om met een dergelijk bereik om te gaan, zijn logaritmische eenheden nuttig: de log van een miljoen is 6, dus deze verhouding vertegenwoordigt een verschil van 120 dB. Het gehoor is niet inherent logaritmisch. (Logaritmische maatstaven zijn ook nuttig wanneer een geluid (kortstondig) exponentieel toeneemt of afneemt in de tijd. Dit gebeurt in veel toepassingen waarbij sprake is van proportionele versterking of proportioneel verlies.)

De gebruikte filters voor dBA en dB(C)

Het meest gebruikte geluidsniveaufilter is de A-schaal, die ruwweg overeenkomt met de inverse van de 40 dB (bij 1 kHz) equal-loudness curve. Bij gebruik van dit filter is de geluidsniveaumeter dus minder gevoelig voor zeer hoge en zeer lage frequenties. Metingen op deze schaal worden uitgedrukt in dBA. De C-schaal varieert weinig over verscheidene octaven en is dus alleen geschikt voor subjectieve metingen bij matige tot hoge geluidsniveaus. Metingen op deze schaal worden uitgedrukt in dB(C). Er is ook een (zelden gebruikte) B wegingsschaal, die het midden houdt tussen A en C. Onderstaande figuur toont de responsie van het A-filter (links) en het C-filter, met de versterking in dB ten opzichte van 1 kHz. (Voor een inleiding tot filters, zie RC-filters, integratoren en differentiatoren).



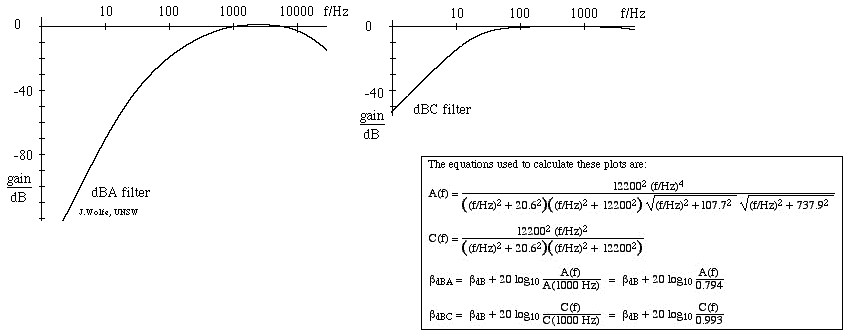
Op de sites voor muziekakoestiek en spraakakoestiek zetten we de geluidsspectra in dB uit. De reden voor deze gangbare praktijk is dat het bereik van de gemeten geluidsdrukken groot is.

dB(G)-metingen maken gebruik van een smalbandfilter dat een hoge weging geeft aan frequenties tussen 1 en 20 Hz, en een lage weging aan andere. Het geeft dus grote waarden voor geluiden en infrageluiden die niet direct hoorbaar zijn. ISO 7196:1995

Luidheid, fon en sone, gehoorresponskrommen

De fon is een eenheid die aan dB is gerelateerd door de psychofysisch gemeten frequentierespons van het oor. Bij 1 kHz zijn de waarden in fon en dB per definitie gelijk. Voor alle andere frequenties wordt de fonschaal bepaald door de resultaten van experimenten waarbij vrijwilligers werd gevraagd de luidheid van een signaal op een bepaalde frequentie aan te passen tot zij oordeelden dat de luidheid ervan gelijk was aan die van een 1 kHz-signaal. Om van dB naar phon om te rekenen, is een grafiek van dergelijke resultaten nodig. Zo’n grafiek is afhankelijk van het geluidsniveau: bij hoge geluidsniveaus wordt hij vlakker.

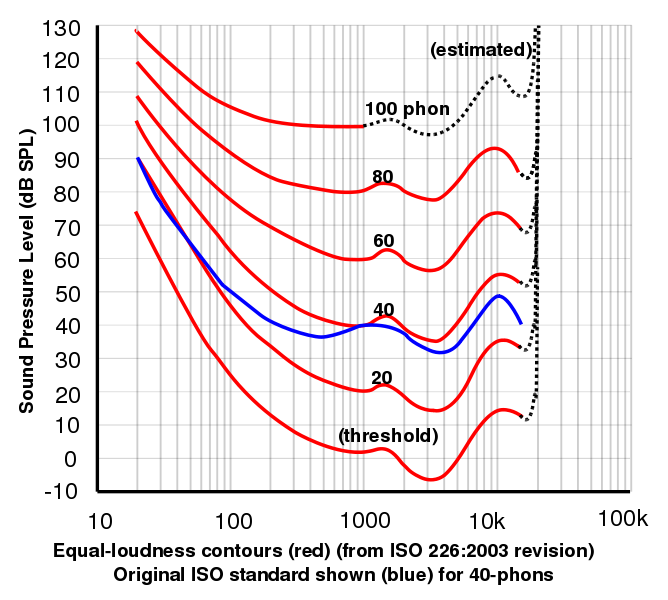
Deze grafiek, met dank aan Lindosland, toont de gegevens uit 2003 van de International Standards Organisation voor krommen van gelijke luidheid die experimenteel zijn bepaald. Grafieken van gelijke luidheid als functie van de frequentie worden vaak algemeen Fletcher-Munson-curven genoemd, naar het oorspronkelijke werk van Fletcher, H. en Munson, W.A. (1933) J.Acoust.Soc.Am. 6:59. U kunt uw eigen curven maken met behulp van onze gehoorrespons site.

De toon is afgeleid van psychofysische metingen waarbij vrijwilligers geluiden aanpassen totdat zij oordelen dat deze twee keer zo luid zijn. Dit maakt het mogelijk de waargenomen luidheid te relateren aan de sone. Eén sone is gedefinieerd als gelijk aan 40 fonen. Experimenteel werd vastgesteld dat boven 40 fonen een toename van het geluidsniveau met 10 dB ongeveer overeenkomt met een waargenomen verdubbeling van de luidheid. Die benadering wordt dus gebruikt bij de definitie van de sone: 1 sone = 40 phon, 2 sone = 50 phon, 4 sone = 60 phon, enz.



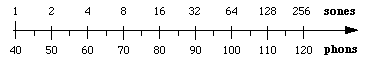
Deze relatie impliceert dat luidheid en intensiteit samenhangen door een machtswet: luidheid in tonen is evenredig met (intensiteit)log 2 = (intensiteit)0,3.

Zou het niet geweldig zijn om te kunnen rekenen van dB (die met een instrument gemeten kunnen worden) naar tonen (die de luidheid benaderen zoals mensen die waarnemen)? Dit wordt soms gedaan met tabellen die je kunt vinden in akoestische handboeken. Als u echter geen bezwaar heeft tegen een nogal grove benadering, kunt u zeggen dat de A-wegingscurve de menselijke frequentierespons bij lage tot matige geluidsniveaus benadert, zodat dB(A) over een beperkt bereik van lage niveaus zeer ruwweg hetzelfde is als sones. Dan kan men de logaritmische relatie tussen sones en phons gebruiken die hierboven is beschreven.

Opnameniveau en decibels

Meters die het opnameniveau of het uitgangsniveau van audio-elektronica (mengpanelen e.d.) meten, meten bijna altijd de AC rms spanning (zie links voor meer informatie over AC en rms). Voor een gegeven weerstand R is het vermogen P V2/R, dus
verschil in spanningsniveau = 20 log (V2/V1) dB = 10 log (V22/V12) dB = 10 log (P2/P1) dB, of

absoluut spanningsniveau = 20 log (V/Vref)

waarbij Vref een referentiespanning is. Dus wat is de referentiespanning?

Het voor de hand liggende niveau om te kiezen is één volt rms, en in dit geval wordt het niveau geschreven als dBV. Dit is rationeel, en ook handig met analoog-digitale kaarten waarvan het maximale bereik vaak ongeveer één volt rms is. Je moet dus het niveau in negatieve dBV houden (minder dan één volt) om de pieken van het signaal niet te clippen, maar niet te negatief (zodat je signaal nog steeds veel groter is dan de achtergrondruis).

Soms zie je dBm. Vroeger betekende dat decibel elektrisch vermogen, ten opzichte van een milliwatt, en soms is dat nog zo. Het is echter om historische redenen ingewikkeld. In het midden van de twintigste eeuw hadden veel audiolijnen een nominale impedantie van 600 Ω. Als de impedantie zuiver resisitief is, en als je V2/600 Ω = 1 mW instelt, dan krijg je V = 0,775 volt. Als u dus een belasting van 600 Ω gebruikte, was 1 mW vermogen 0 dBm, wat overeenkwam met 0,775 V, zodat u uw niveaumeters op die manier ijkte. Het probleem ontstond omdat, als een niveaumeter die spanning meet eenmaal op deze manier is gekalibreerd, hij 0 dBm zal aflezen bij 0,775 V, zelfs als hij niet is aangesloten op 600 Ω. Dus, misschien onlogisch, dBm zal soms dB betekenen ten opzichte van 0,775 V. (Toen ik een jongen was, waren rekenmachines duur, dus gebruikte ik vaders oude rekenliniaal, waarop de factor 0,775 in het cursorvenster was aangegeven om dergelijke berekeningen te vergemakkelijken).

Hoe zet je dBV of dBm om in dB van geluidsniveau? Er is geen eenvoudige manier. Het hangt er van af hoe je het elektrisch vermogen omzet in geluidsvermogen. Zelfs als je het elektrische signaal rechtstreeks op een luidspreker aansluit, zal de omzetting afhangen van het rendement en de impedantie van je luidspreker. En natuurlijk kan er een eindversterker zijn, en diverse akoestische complicaties tussen waar je de dBV op de mengtafel meet en waar je oren zich in het geluidsveld bevinden.

Intensiteit, straling en dB

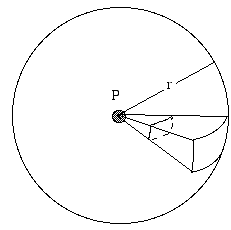
Hoe hangt het geluidsniveau (of het niveau van het radiosignaal, enz.) af van de afstand tot de bron?

Een bron die in alle richtingen evenveel straling uitzendt, wordt isotroop genoemd. Stel u een geïsoleerde geluidsbron voor, ver van enig weerkaatsend oppervlak – misschien een vogel die hoog in de lucht zingt. Stel je een bol voor met straal r, gecentreerd op de bron. De bron zendt voortdurend een totaal vermogen P uit. Dit geluidsvermogen verspreidt zich en gaat door het oppervlak van de bol. Indien de bron isotroop is, is de intensiteit I per definitie overal op dit oppervlak gelijk. De intensiteit I wordt gedefinieerd als het vermogen per oppervlakte-eenheid. De oppervlakte van de bol is 4πr2, dus het vermogen (in ons voorbeeld het geluidsvermogen) dat door elke vierkante meter van het oppervlak gaat, is per definitie

I = P/4πr2.

Wij zien dus dat, voor een isotrope bron, de intensiteit omgekeerd evenredig is met het kwadraat van de afstand tot de bron:

I2/I1 = r12/r22.

Maar de intensiteit is evenredig met het kwadraat van de geluidsdruk, dus kunnen we ook schrijven:

p2/p1 = r1/r2.

Dus als we de afstand verdubbelen, verminderen we de geluidsdruk met een factor 2 en de intensiteit met een factor 4: met andere woorden, we verminderen het geluidsniveau met 6 dB. Als we r met een factor 10 verhogen, verlagen we het niveau met 20 dB, enz.

Wees er echter voor gewaarschuwd dat veel bronnen niet isotroop zijn, vooral als de golflengte kleiner is dan, of van een grootte vergelijkbaar met die van de bron. Verder zijn reflecties vaak heel belangrijk, vooral als de grond dichtbij is, of als je binnenshuis bent.

Druk, intensiteit en specifieke impedantie

Voor akoestische golven wordt de specifieke akoestische impedantie z gedefinieerd als de verhouding van de akoestische druk p tot de gemiddelde deeltjessnelheid u, ten gevolge van het geluid ave, z = p/u . In Akoestische impedantie, intensiteit en vermogen laten we zien hoe de RMS akoestische druk p en de intensiteit I met elkaar in verband kunnen worden gebracht:
I = p2/z

Voor lucht bedraagt de specifieke akoestische impedantie z 420 kg.s-1.m-2 = 420 Pa.s.m-1. Voor (zoet) water is de specifieke akoestische impedantie 1,48 MPa.s.m-1. Een geluidsgolf in water met dezelfde druk heeft dus een veel lagere intensiteit dan een geluidsgolf in lucht.

dBi en straling die varieert met de richting

Straling die varieert met de richting wordt anisotroop genoemd. In veel gevallen van communicatie is isotrope straling verspilling: waarom een aanzienlijk deel van het vermogen naar boven uitzenden als de ontvanger zich, zoals u, relatief dicht bij de grond bevindt. Voor geluid met een korte golflengte (waaronder het grootste deel van het voor spraak belangrijke bereik) kan een megafoon helpen uw stem meer anisotroop te maken. Voor radio is er een breed scala van ontwerpen waarmee antennes zeer anisotroop kunnen zijn, zowel voor zenden als ontvangen.

Dus, als je geïnteresseerd bent in uitzending in (of ontvangst uit) een bepaalde richting, wil je dat de verhouding van de intensiteit gemeten in die richting, op een bepaalde afstand, hoger is dan die gemeten op dezelfde afstand van een isotrope straler (of ontvangen door een isotrope ontvanger). Deze verhouding wordt de versterking genoemd; druk de verhouding uit in dB en je hebt de versterking in dBi voor die straler. Deze eenheid wordt vooral gebruikt voor antennes, zowel voor zenden als ontvangen, maar soms ook voor geluidsbronnen en richtmicrofoons.

Voorbeeldproblemen

Een paar mensen hebben geschreven met de vraag om voorbeelden bij het gebruik van dB in berekeningen. Dus…
• Al het andere gelijk, hoeveel luider wordt een luidspreker (in zijn lineaire bereik) aangestuurd door een 100 W versterker dan door een 10 W versterker?

  De vermogens verschillen met een factor tien, wat, zoals we hierboven zagen, 10 dB is. Verder gelijk betekent hier dat de frequentierespons gelijk is en dat hetzelfde ingangssignaal wordt gebruikt, enz. De frequentie-afhankelijkheid moet dus gelijk zijn. 10 dB komt overeen met 10 fonen. Om een waargenomen verdubbeling van luidheid te krijgen, heb je een toename van 10 fonen nodig. Dus de luidspreker die wordt aangestuurd door de 100 W versterker is twee keer zo luid als wanneer hij wordt aangestuurd door de 10 W, ervan uitgaande dat je in het lineaire bereik blijft en de luidspreker niet vervormt of kapot maakt. (De 100 W versterker produceert tweemaal zoveel tonen als de 10 W.)

• Ik sta op een afstand R van een kleine geluidsbron (grootte veel kleiner dan R), op grondniveau in de open lucht waar reflecties kunnen worden verwaarloosd. Het geluidniveau is L. Als ik nu naar een afstand nR ga (n een getal, en nR nog steeds veel groter dan de grootte van de bron), wat is dan het nieuwe geluidniveau?

  Eerst moet worden opgemerkt dat het verwaarlozen van reflecties zeer belangrijk is. Deze berekening werkt niet in een kamer, waar reflecties tegen de muur (die samen galm veroorzaken) de berekening bemoeilijken. In de open lucht is de geluidsintensiteit evenredig met 1/r2, waarbij r de afstand tot de bron is. (De evenredigheidsconstante hangt af van hoe goed de grond weerkaatst, en is hier niet van belang, omdat deze bij de berekening ruwweg zal wegvallen, mits r redelijk groot is). Dus, als we r verhogen van R tot nR, verlagen we de intensiteit van I tot I/n 2.

  Het verschil in decibels tussen de twee signalen met intensiteit I 2 en I 1 is hierboven gedefinieerd als

  ΔL = 10 log (I2/I1) = 10 log ((I/n 2)/I) = 10 log (1/n 2) = -10 log (n 2) = -20 log n.

  Bij voorbeeld, als n 2 is (d.w.z. als we twee keer zo ver weg gaan), wordt de intensiteit met een factor vier verminderd en daalt het geluidsniveau van L tot (L – 6dB).

• Als een jong iemand in ideale stille omstandigheden een toon van 1 kHz bij 0 dB kan horen die door een luidspreker (misschien een softspeaker?) wordt uitgezonden, met hoeveel moet dan het vermogen van de luidspreker worden verhoogd om het geluid op 110 dB te brengen (een gevaarlijk luid maar overleefbaar niveau)?

  Het verschil in decibels tussen de twee signalen met de vermogens P2 en P1 is hierboven gedefinieerd als

  ΔL = 10 log (P2/P1) dB, dus als we deze twee gelijke grootheden met 10 tot de macht verheffen:
  10L/10 = P2/P1 dus:
  P2/P1 = 10110/10 = 1011 = honderdduizend miljoen.

  waarmee wordt aangetoond dat het menselijk oor een opmerkelijk groot dynamisch bereik heeft, misschien wel groter dan dat van het oog.

• Een versterker heeft een ingang van 10 mV en een uitgang van 2 V. Wat is de spanningsversterking in dB?

  Voltage verschijnt, net als druk, in het kwadraat in uitdrukkingen voor vermogen of intensiteit. (Het vermogen gedissipeerd in een weerstand R is V2/R.) Dus, volgens afspraak, definiëren we:

  gain = 20 log (Vout/Vin)
  = 20 log (2V/10mV)
  = 46 dB

  (In de hierboven gegeven akoestische gevallen zagen we dat de drukverhouding, uitgedrukt in dB, dezelfde was als de vermogensverhouding: dat was de reden voor de factor 20 bij het definiëren van dB voor druk. Het is de moeite waard op te merken dat in het voorbeeld van de spanningsversterking de vermogensversterking van de versterker waarschijnlijk niet gelijk zal zijn aan de spanningsversterking, die wordt gedefinieerd door de hier gebruikte conventie. Het vermogen is evenredig met het kwadraat van de spanning in een gegeven weerstand. De ingangs- en uitgangsimpedanties van versterkers zijn echter vaak heel verschillend. Een bufferversterker of emittervolger heeft bijvoorbeeld een spanningsversterking van ongeveer 1, maar een grote stroomversterking).

• Wat is het verschil, in dB, tussen de bestralingssterkte (lichtintensiteit) op aarde (8,3 lichtminuten van de zon) en op Uranus (160 lichtminuten)?

  Zoals bij geluid neemt de isotrope lichtintensiteit af als r-2, dus de intensiteitsverhouding is (160/8.3)2 = 20 log (160/8.3) = 26 dB.

Gezondheid en veiligheid op het werk

Verschillende landen en provincies hebben uiteraard verschillende wetten betreffende blootstelling aan lawaai op het werk, die met wisselend enthousiasme worden gehandhaafd. Veel van deze wetten hebben een limiet voor blootstelling aan continu lawaai van 85 dB(A), voor een dienst van 8 uur. Voor elke 3 dB toename wordt de toegestane blootstelling gehalveerd. Dus als je in een nachtclub werkt waar versterkte muziek 100 dB(A) in de buurt van je oren produceert, is de toegestane blootstelling 15 minuten. Er is een limiet voor impulslawaai zoals vuurwapens of gereedschap dat explosieve schoten gebruikt. (b.v. 140 dB piek mag op geen enkel moment van de dag worden overschreden.) Er zijn veel documenten met advies over hoe blootstelling aan lawaai kan worden verminderd bij de bron (b.v. het muziekniveau zachter zetten), tussen de bron en het oor (b.v. bij een concert uit de buurt van de luidsprekers gaan staan) en bij het oor (b.v. oordopjes of industriële gehoorbeschermers dragen). Lawaaibeheersing en bescherming van het gehoor op het werk is de gedragscode in de staat New South Wales, Australië (adres van de auteur).

Enkele FAQs

• Hoe luid is een vliegtuig? Een trein? Een persoon die zingt? Een hond die blaft? Een elektrisch gereedschap? De antwoorden op deze vraag lopen sterk uiteen. Het hangt sterk af van hoe ver je weg bent, of je al dan niet binnen bent, of er nagalm is, hoe sterk de bron in kwestie is en wat zijn spectrum is. Waarden geven zonder zeer specifiek te zijn over de omstandigheden zou enigszins misleidend zijn. Omdat de rest van deze pagina bedoeld is om betrouwbaar te zijn, voor zover dat gaat, geef ik hier liever geen waarden.
• Hoe “telt men decibels bij elkaar op”, d.w.z. Welk geluidsniveau krijgt men als men niveau a bij niveau b optelt? Als de bronnen coherent zijn (wat meestal betekent dat ze uiteindelijk van dezelfde bron komen), dan kunnen er ingewikkelde interferentie-effecten zijn. In de meeste gevallen, wanneer de bronnen onafhankelijk zijn, kan men de intensiteiten optellen en dan omrekenen naar decibels. Als men echter de geluidsniveaus in dB(A) krijgt, is het niet zo gemakkelijk om terug te gaan naar de intensiteit, en moet men iets weten over het spectrum van het geluid. Als je de verdeling van het geluid in verschillende frequentiebanden kent, kun je de applet op deze link gebruiken.
• Some of the questions on our FAQ in music acoustics relate to decibels, including
  • Why do the sounds of two musical instruments always reinforce, and never cancel out?
  • How much does one more violin add to the sound level of a section of n violins?
  • Does adding two equal sounds give an increase of 3 or 6 dB? Why?
  • What is the loudest sound?
  • Is there really no sound in space?

Related pages

• Measure your own hearing response
• Adding sound levels from incoherent sources
• What are interference beats and Tartini tones?
• FAQ in music acoustics
• Loudness and spectra: how spectral content and other features are related to loudness
• Formants: what are they? A discussion of the different meanings of this term
• Music acoustics home page
• Physclips: a multi-level, multimedia introduction to mechanics.
• A list of other educational web sites from this author.