10.13: Die Avogadrosche Hypothese und das molare Volumen

admin

Die Avogadrosche Hypothese und das molare Volumen

Das Volumen ist nach der Stückzahl und der Masse eine dritte Möglichkeit, die Menge eines Stoffes zu messen. Bei Flüssigkeiten und Feststoffen hängt das Volumen stark von der Dichte des Stoffes ab. Das liegt daran, dass feste und flüssige Teilchen dicht aneinander gepackt sind und nur sehr wenig Raum zwischen den Teilchen vorhanden ist. Gase bestehen jedoch größtenteils aus leeren Räumen zwischen den eigentlichen Gasteilchen (siehe Abbildung unten).

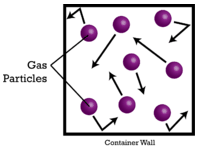
Abbildung \(\PageIndex{1}\): Gasteilchen sind sehr klein im Vergleich zu den großen Mengen an leerem Raum zwischen ihnen.

Im Jahr 1811 erklärte Amadeo Avogadro, dass die Volumina aller Gase leicht bestimmt werden können. Die Avogadro-Hypothese besagt, dass alle Gase bei gleicher Temperatur und gleichem Druck die gleiche Anzahl von Teilchen enthalten. Da das Gesamtvolumen eines Gases in erster Linie aus dem leeren Raum zwischen den Teilchen besteht, ist die tatsächliche Größe der Teilchen selbst nahezu vernachlässigbar. Ein bestimmtes Volumen eines Gases mit kleinen leichten Teilchen wie Wasserstoff \(\ce{H_2} \right)\) enthält die gleiche Anzahl von Teilchen wie das gleiche Volumen eines schweren Gases mit großen Teilchen wie Schwefelhexafluorid, \(\ce{SF_6}\).

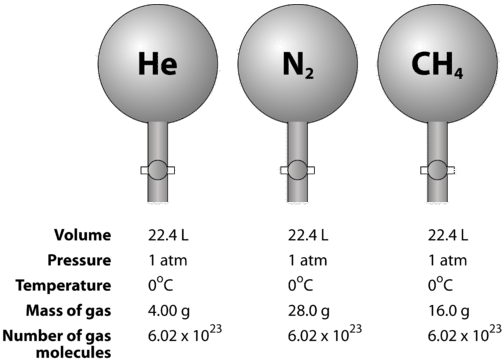
Gase sind komprimierbar, d. h., wenn sie unter hohen Druck gesetzt werden, werden die Teilchen näher zueinander gezwungen. Dadurch verringert sich die Menge des leeren Raums und das Volumen des Gases. Das Gasvolumen wird auch durch die Temperatur beeinflusst. Wenn ein Gas erhitzt wird, bewegen sich seine Moleküle schneller und das Gas dehnt sich aus. Da sich das Gasvolumen aufgrund von Druck- und Temperaturänderungen ändert, muss der Vergleich der Gasvolumina bei einer Standardtemperatur und einem Standarddruck durchgeführt werden. Die Standardtemperatur und der Standarddruck (STP) sind definiert als \(0^\text{o} \text{C}\) \(\left( 273.15 \: \text{K} \right)\) und \(1 \: \text{atm}\) Druck. Das molare Volumen eines Gases ist das Volumen eines Mols eines Gases bei STP. Bei STP nimmt ein Mol (\( 6,02 \mal 10^{23}\) repräsentative Teilchen) eines Gases ein Volumen von \(22,4 \: \text{L}\) ein (Abbildung unten).

Abbildung \(\PageIndex{2}\): Ein Mol eines beliebigen Gases nimmt \(22,4 \: \text{L}\) bei Standardtemperatur und -druck (\(0^\text{o} \text{C}\) und \(1 \: \text{atm}\)) ein.

Die folgende Abbildung veranschaulicht, wie das molare Volumen beim Vergleich verschiedener Gase zu sehen ist. Die Proben von Helium \(\left( \ce{He} \right)\), Stickstoff \(\left( \ce{N_2} \right)\) und Methan \(\left( \ce{CH_4} \right)\) befinden sich bei STP. Jedes enthält 1 Mol oder \(6,02 \mal 10^{23}\) Teilchen. Die Masse der einzelnen Gase ist jedoch unterschiedlich und entspricht der molaren Masse des jeweiligen Gases: \(4,00 \: \text{g/mol}\) für \(\ce{He}\), \(28,0 \: \text{g/mol}\) für \(\ce{N_2}\), und \(16,0 \: \text{g/mol}\) für \(\ce{CH_4}\).

Abbildung \(\PageIndex{3}\): Die Avogadro-Hypothese besagt, dass gleiche Volumina eines beliebigen Gases bei gleicher Temperatur und gleichem Druck die gleiche Anzahl von Teilchen enthalten. Bei Standardtemperatur und -druck nimmt 1 Mol eines beliebigen Gases \(22,4 \: \text{L}\) ein.