Arten der Interpolation – Vorteile und Nachteile
Interpolationsmethoden
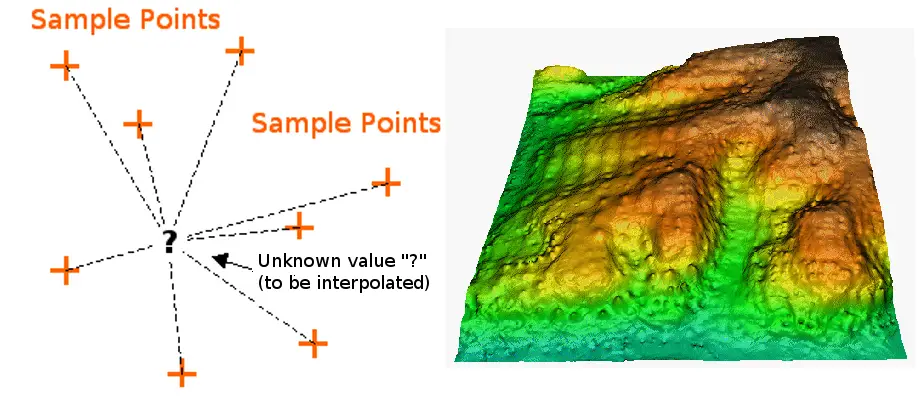
Interpolation ist der Prozess der Verwendung von Punkten mit bekannten Werten oder Stichprobenpunkten zur Schätzung von Werten an anderen unbekannten Punkten. Sie kann zur Vorhersage unbekannter Werte für beliebige geografische Punktdaten verwendet werden, wie z. B. Höhe, Niederschlag, chemische Konzentrationen, Lärmpegel usw.
Die verfügbaren Interpolationsmethoden sind nachstehend aufgeführt.
Inverse Distance Weighted (IDW)
Der Interpolator mit inverser Abstandsgewichtung geht davon aus, dass jeder Eingabepunkt einen lokalen Einfluss hat, der mit der Entfernung abnimmt. Er gewichtet die Punkte, die näher an der Verarbeitungszelle liegen, stärker als die weiter entfernten. Eine bestimmte Anzahl von Punkten oder alle Punkte innerhalb eines bestimmten Radius können verwendet werden, um den Ausgabewert für jeden Ort zu bestimmen. Bei dieser Methode wird davon ausgegangen, dass der Einfluss der Variable, die abgebildet werden soll, mit der Entfernung von ihrem Abtastort abnimmt.
IDW Interpolation; Mit freundlicher Genehmigung: QGIS
Der Algorithmus der inversen Abstandsgewichtung (IDW) ist im Grunde ein Interpolator des gleitenden Mittelwerts, der in der Regel auf stark veränderliche Daten angewendet wird. Bei bestimmten Datentypen ist es möglich, zur Erfassungsstelle zurückzukehren und einen neuen Wert aufzuzeichnen, der sich statistisch vom ursprünglichen Messwert unterscheidet, aber innerhalb des allgemeinen Trends für das Gebiet liegt.
Die interpolierte Fläche, die mit einem gleitenden Mittelwert geschätzt wird, ist kleiner als der lokale Maximalwert und größer als der lokale Minimalwert.

IDW Interpolated Surface; Courtesy:ESRI
IDW Interpolation setzt explizit die Annahme um, dass Dinge, die nahe beieinander liegen, sich ähnlicher sind als solche, die weiter voneinander entfernt sind. Um einen Wert für eine nicht gemessene Stelle vorherzusagen, verwendet IDW die Messwerte in der Umgebung der Vorhersagestelle. Die Messwerte, die dem Vorhersageort am nächsten liegen, haben einen größeren Einfluss auf den vorhergesagten Wert als die weiter entfernten. IDW geht also davon aus, dass jeder Messpunkt einen lokalen Einfluss hat, der mit der Entfernung abnimmt. Die IDW-Funktion sollte verwendet werden, wenn die Punktmenge dicht genug ist, um das Ausmaß der für die Analyse erforderlichen lokalen Oberflächenvariation zu erfassen. IDW bestimmt Zellwerte unter Verwendung eines linear gewichteten Kombinationssatzes von Probenpunkten. Dabei werden die Punkte, die näher an der Vorhersageposition liegen, stärker gewichtet als die weiter entfernten, daher der Name „inverse distance weighted“
Das IDW-Verfahren berechnet einen Wert für jeden Gitterknoten, indem es die umgebenden Datenpunkte untersucht, die innerhalb eines benutzerdefinierten Suchradius liegen. Einige oder alle Datenpunkte können für den Interpolationsprozess verwendet werden. Der Knotenwert wird durch Mittelwertbildung der gewichteten Summe aller Punkte berechnet. Datenpunkte, die zunehmend weiter vom Knoten entfernt liegen, beeinflussen den berechneten Wert weit weniger als solche, die näher am Knoten liegen.
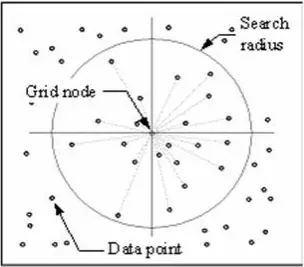
Um jeden Gitterknoten wird ein Radius erzeugt, aus dem Datenpunkte für die Berechnung ausgewählt werden. Options to control the use of IDW include power, search radius, fixed search radius, variable search radius and barrier.
Note: The optimal power (p) value is determined by minimizing the root mean square prediction error (RMSPE).
Advantages
- Can estimate extreme changes in terrain such as: Cliffs, Fault Lines.
- Dense evenly space points are well interpolated (flat areas with cliffs).
- Can increase or decrease amount of sample points to influence cell values.
Disadvantages
- Cannot estimate above maximum or below minimum values.
- Not very good for peaks or mountainous areas.
Natural Neighbour Inverse Distance Weighted (NNIDW)
Natural neighbor interpolation has many positive features, can be used for both interpolation and extrapolation, and generally works well with clustered scatter points. Die Grundgleichung der natürlichen Nachbarschaftsinterpolation ist identisch mit der der IDW-Interpolation und stellt eine weitere gewichtete Durchschnittsmethode dar. Diese Methode kann große Punktedatensätze effizient verarbeiten. Bei der Natural Neighbor-Methode definieren lokale Koordinaten den Einfluss, den jeder Streupunkt auf die Ausgabezellen hat.
Die Natural Neighbour-Methode ist eine geometrische Schätzungstechnik, die natürliche Nachbarschaftsregionen verwendet, die um jeden Punkt im Datensatz herum erzeugt werden.
Wie IDW ist diese Interpolationsmethode eine Methode der gewichteten Durchschnittsinterpolation. Anstatt jedoch den Wert eines interpolierten Punktes unter Verwendung aller Eingangspunkte, gewichtet nach ihrer Entfernung, zu ermitteln, erstellt die Natural Neighbors-Interpolation eine Delauney-Triangulation der Eingangspunkte und wählt die nächstgelegenen Knoten aus, die eine konvexe Hülle um den Interpolationspunkt bilden, und gewichtet dann ihre Werte nach der proportionalen Fläche. Diese Methode ist am besten geeignet, wenn die Stichprobenpunkte mit ungleichmäßiger Dichte verteilt sind. Sie ist eine gute Allzweck-Interpolationstechnik und hat den Vorteil, dass Sie keine Parameter wie Radius, Anzahl der Nachbarn oder Gewichte angeben müssen.

Natürliches IDW: Mit freundlicher Genehmigung: ESRI
Dieses Verfahren berücksichtigt lokale Minimal- und Maximalwerte in der Punktdatei und kann so eingestellt werden, dass Überschreitungen lokaler Höchstwerte und Unterschreitungen lokaler Tiefstwerte begrenzt werden. Die Methode ermöglicht so die Erstellung von genauen Oberflächenmodellen aus Datensätzen, die sehr spärlich verteilt sind oder eine sehr lineare räumliche Verteilung aufweisen.
Vorteile
- Effiziente Handhabung einer großen Anzahl von Messpunkten.
Spline
Spline schätzt Werte mit Hilfe einer mathematischen Funktion, die die Gesamtkrümmung der Oberfläche minimiert, was zu einer glatten Oberfläche führt, die genau durch die Eingabepunkte verläuft.

Spline: Courtesy: ESRI
Konzeptionell entspricht es der Biegung eines Gummibandes durch bekannte Punkte bei gleichzeitiger Minimierung der Gesamtkrümmung der Oberfläche. Es passt eine mathematische Funktion an eine bestimmte Anzahl nächstgelegener Eingabepunkte an, während es durch die Probepunkte verläuft. Diese Methode eignet sich am besten für sanft schwankende Oberflächen, wie z. B. Erhebungen, Grundwasserhöhen oder Schadstoffkonzentrationen.
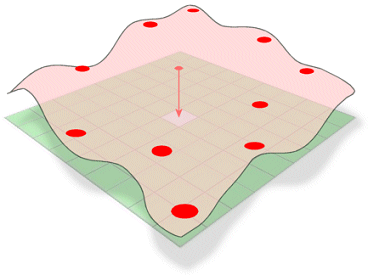
Die Spline-Methode der Interpolation schätzt unbekannte Werte durch Biegen einer Fläche durch bekannte Werte.
Es gibt zwei Spline-Methoden: die regularisierte und die Spannungsmethode.
Die regularisierte Methode erzeugt eine glatte, sich allmählich verändernde Oberfläche mit Werten, die außerhalb des Bereichs der Stichprobendaten liegen können. Sie bezieht die erste Ableitung (Steigung), die zweite Ableitung (Änderungsrate der Steigung) und die dritte Ableitung (Änderungsrate der zweiten Ableitung) in ihre Minimierungsberechnungen ein.
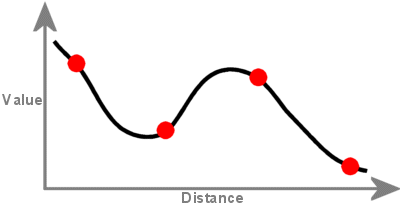
Eine mit Spline-Interpolation erstellte Fläche geht durch jeden Abtastpunkt und kann den Wertebereich des Abtastpunktsatzes überschreiten.
Obwohl ein Tension-Spline nur erste und zweite Ableitungen verwendet, bezieht er mehr Punkte in die Spline-Berechnungen ein, was in der Regel glattere Oberflächen erzeugt, aber die Berechnungszeit erhöht.
Diese Methode zieht eine Oberfläche über die erfassten Punkte, was zu einem gestreckten Effekt führt. Spline verwendet gekrümmte Linien (Curvilinear Lines-Methode) zur Berechnung der Zellwerte.
Wählen einer Gewichtung für Spline-Interpolationen
Regularisierter Spline: Je höher die Gewichtung, desto glatter die Oberfläche. Geeignet sind Gewichte zwischen 0 und 5. Typische Werte sind 0, 0,001, 0,01, 0,1 und 0,5.
Spannungsspline: Je höher die Gewichtung ist, desto gröber ist die Oberfläche und desto mehr stimmen die Werte mit dem Bereich der Probendaten überein. Die Gewichtswerte müssen größer oder gleich Null sein. Typical values are 0, 1, 5, and 10.
Advantages
- Useful for estimating above maximum and below minimum points.
- Creates a smooth surface effect.
Disadvantages
- Cliffs and fault lines are not well presented because of the smoothing effect.
- When the sample points are close together and have extreme differences in value, Spline interpolation doesn’t work as well. This is because Spline uses slope calculations (change over distance) to figure out the shape of the flexible rubber sheet.
Kriging
Kriging is a geostatistical interpolation technique that considers both the distance and the degree of variation between known data points when estimating values in unknown areas. A kriged estimate is a weighted linear combination of the known sample values around the point to be estimated.
Kriging-Verfahren, das eine geschätzte Fläche aus einer verstreuten Menge von Punkten mit z-Werten erzeugt. Kriging geht davon aus, dass der Abstand oder die Richtung zwischen Stichprobenpunkten eine räumliche Korrelation widerspiegelt, die zur Erklärung von Variationen in der Oberfläche verwendet werden kann. Das Kriging-Werkzeug passt eine mathematische Funktion an eine bestimmte Anzahl von Punkten oder an alle Punkte innerhalb eines bestimmten Radius an, um den Ausgabewert für jeden Ort zu bestimmen. Kriging ist ein mehrstufiger Prozess; er umfasst die explorative statistische Analyse der Daten, die Variogrammmodellierung, die Erstellung der Oberfläche und (optional) die Erkundung einer Varianzoberfläche. Kriging ist am besten geeignet, wenn bekannt ist, dass die Daten eine räumlich korrelierte Distanz oder eine Richtungsabweichung aufweisen. Es wird häufig in der Bodenkunde und Geologie verwendet.
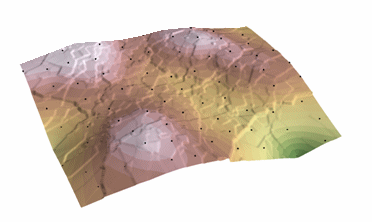
Kriging: Courtesy: ESRI
The predicted values are derived from the measure of relationship in samples using sophisticated weighted average technique. It uses a search radius that can be fixed or variable. The generated cell values can exceed value range of samples, and the surface does not pass through samples.
The Kriging Formula
Kriging is similar to IDW in that it weights the surrounding measured values to derive a prediction for an unmeasured location. The general formula for both interpolators is formed as a weighted sum of the data:
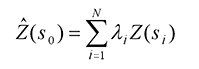
- where:
Z(si) = the measured value at the ith location
λi = an unknown weight for the measured value at the ith location
s0 = the prediction location
N = the number of measured values
In IDW, the weight, λi, depends solely on the distance to the prediction location. Bei der Kriging-Methode basieren die Gewichte jedoch nicht nur auf dem Abstand zwischen den gemessenen Punkten und dem Vorhersageort, sondern auch auf der gesamten räumlichen Anordnung der gemessenen Punkte. Um die räumliche Anordnung in den Gewichten zu verwenden, muss die räumliche Autokorrelation quantifiziert werden. Beim gewöhnlichen Kriging hängt das Gewicht λi also von einem an die Messpunkte angepassten Modell, der Entfernung zum Vorhersageort und den räumlichen Beziehungen zwischen den Messwerten um den Vorhersageort ab. In den folgenden Abschnitten wird erläutert, wie die allgemeine Kriging-Formel verwendet wird, um eine Karte der Vorhersagefläche und eine Karte der Genauigkeit der Vorhersagen zu erstellen.
Typen von Kriging
Ordinäres Kriging
Ordinäres Kriging geht von dem Modell
Z(s) = µ + ε(s),
aus, bei dem µ eine unbekannte Konstante ist. Eine der Hauptfragen beim gewöhnlichen Kriging ist, ob die Annahme eines konstanten Mittelwerts sinnvoll ist. Sometimes there are good scientific reasons to reject this assumption. However, as a simple prediction method, it has remarkable flexibility.
Ordinary kriging can use either semivariograms or covariances, use transformations and remove trends, and allow for measurement error.
Simple Kriging
Simple kriging assumes the model
Z(s) = µ + ε(s),
where µ is a known constant.
Simple kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Universal Kriging
Universal kriging assumes the model
Z(s) = µ(s) + ε(s),
where µ(s) is some deterministic function.
Universal kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Indikator-Kriging
Indikator-Kriging geht von dem Modell
I(s) = µ + ε(s),
aus, wobei µ eine unbekannte Konstante und I(s) eine binäre Variable ist. Die Erzeugung binärer Daten kann durch die Verwendung eines Schwellenwerts für kontinuierliche Daten erfolgen, oder es kann sein, dass die beobachteten Daten 0 oder 1 sind. Beispielsweise könnte eine Stichprobe aus Informationen darüber bestehen, ob ein Punkt ein bewaldeter oder nicht bewaldeter Lebensraum ist, wobei die binäre Variable die Klassenzugehörigkeit angibt. Bei der Verwendung binärer Variablen geht das Indikator-Kriging genauso vor wie das gewöhnliche Kriging.
Das Indikator-Kriging kann entweder Semivariogramme oder Kovarianzen verwenden.
Probability Kriging
Probability Kriging geht von dem Modell aus
I(s) = I(Z(s) > ct) = µ1 + ε1(s)Z(s) = µ2 + ε2(s),
wobei µ1 und µ2 unbekannte Konstanten sind und I(s) eine binäre Variable ist, die durch Verwendung eines Schwellenindikators erzeugt wird, I(Z(s) > ct). Man beachte, dass es jetzt zwei Arten von Zufallsfehlern gibt, ε1(s) und ε2(s), so dass es für jeden von ihnen eine Autokorrelation und eine Kreuzkorrelation zwischen ihnen gibt. Das Wahrscheinlichkeits-Kriging versucht dasselbe wie das Indikator-Kriging zu erreichen, verwendet aber das Kokriging, um eine bessere Leistung zu erzielen.
Das Wahrscheinlichkeits-Kriging kann entweder Semivariogramme oder Kovarianzen, Kreuzkovarianzen und Transformationen verwenden, kann aber keine Messfehler berücksichtigen.
style=“display:inline-block;width:468px;height:60px“ data-ad-client=“ca-pub-7134201556760050″ data-ad-slot=“9271753327″>
Disjunctive Kriging
Disjunctive Kriging setzt das Modell
f(Z(s)) = µ1 + ε(s),
wobei µ1 eine unbekannte Konstante und f(Z(s)) eine beliebige Funktion von Z(s) ist. Beachten Sie, dass Sie f(Z(s)) = I(Z(s) > ct) schreiben können, so dass das Indikator-Kriging ein Spezialfall des disjunktiven Krigings ist. In Geostatistical Analyst kann man mit disjunktem Kriging entweder den Wert selbst oder einen Indikator vorhersagen.
Im Allgemeinen versucht das disjunktive Kriging mehr zu leisten als das gewöhnliche Kriging. Die Vorteile mögen zwar größer sein, aber auch die Kosten sind höher. Disjunctive kriging requires the bivariate normality assumption and approximations to the functions fi(Z(si)); the assumptions are difficult to verify, and the solutions are mathematically and computationally complicated.
Disjunctive kriging can use either semivariograms or covariances and transformations, but it cannot allow for measurement error.
Advantages
- Directional influences can be accounted for: Soil Erosion, Siltation Flow, Lava Flow and Winds.
- Exceeds the minimum and maximum point values
Disadvantages
- Does not pass through any of the point values and causes interpolated values to be higher or lower then real values.
Um einen tieferen Einblick in den mathematischen Ansatz von Kriging zu erhalten, klicken Sie bitte auf Kriging eine Interpolationsmethode.
PointInterp
Eine Methode, die IDW ähnelt, die Funktion PointInterp ermöglicht eine bessere Kontrolle über die Stichprobenumgebung. Der Einfluss einer bestimmten Stichprobe auf den interpolierten Gitterzellenwert hängt davon ab, ob der Stichprobenpunkt in der Nachbarschaft der Zelle liegt und wie weit er von der zu interpolierenden Zelle entfernt ist. Punkte außerhalb der Nachbarschaft haben keinen Einfluss.

PointInterp; Mit freundlicher Genehmigung: ESRI
Der gewichtete Wert der Punkte innerhalb der Nachbarschaft wird durch eine inverse abstandsgewichtete Interpolation oder eine inverse exponentielle Abstandsinterpolation berechnet. Bei dieser Methode wird ein Raster anhand von Punktmerkmalen interpoliert, wobei jedoch verschiedene Arten von Nachbarschaften möglich sind. Nachbarschaften können Formen wie Kreise, Rechtecke, unregelmäßige Polygone, Ringformen oder Keile haben.
Trend
Trend ist eine statistische Methode, die die Fläche findet, die zu den Stichprobenpunkten passt, indem sie eine Regressionsanpassung im kleinsten Quadrat verwendet. Dabei wird eine Polynomgleichung an die gesamte Fläche angepasst. Das Ergebnis ist eine Oberfläche, die die Varianz der Oberfläche im Verhältnis zu den Eingabewerten minimiert. Die Oberfläche wird so konstruiert, dass für jeden Eingabepunkt die Summe der Differenzen zwischen den tatsächlichen Werten und den geschätzten Werten (d. h. die Varianz) so klein wie möglich ist.

Trend; Courtsey:ESRI
Es handelt sich um einen ungenauen Interpolator, und die resultierende Oberfläche geht selten durch die Eingabepunkte. Diese Methode erkennt jedoch Trends in den Beispieldaten und ähnelt natürlichen Phänomenen, die in der Regel gleichmäßig variieren.
Vorteil
- Trendflächen sind gut geeignet, um grobe Muster in den Daten zu erkennen; die interpolierte Fläche geht selten durch die Probenpunkte.
Topo to Raster
Durch die Interpolation von Höhenwerten für ein Raster erlegt die Topo to Raster-Methode Beschränkungen auf, die ein hydrologisch korrektes digitales Höhenmodell gewährleisten, das eine zusammenhängende Entwässerungsstruktur enthält und Höhenrücken und Bäche aus den eingegebenen Konturdaten korrekt darstellt. Sie verwendet eine iterative Finite-Differenzen-Interpolationstechnik, die die Recheneffizienz der lokalen Interpolation optimiert, ohne die Oberflächenkontinuität der globalen Interpolation zu verlieren. Es wurde speziell entwickelt, um intelligent mit Konturdaten zu arbeiten.
Unten sehen Sie ein Beispiel für eine Oberfläche, die aus Höhenpunkten, Höhenlinien, Flusslinien und See-Polygonen mit Hilfe der Topo to Raster Interpolation interpoliert wurde.
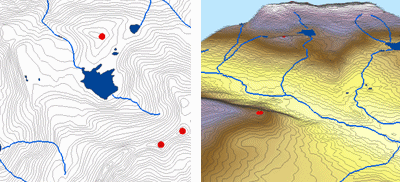
Topo zu Raster; Mit freundlicher Genehmigung: ESRI
Topo to Raster ist ein spezialisiertes Werkzeug zur Erstellung hydrologisch korrekter Rasterflächen aus Vektordaten von Geländekomponenten wie Höhenpunkten, Höhenlinien, Bachlinien, Seepolygonen, Senkenpunkten und Untersuchungsgebietsgrenzenpolygonen.
Dichte
Dichte-Werkzeuge (verfügbar in ArcGIS) erzeugen eine Fläche, die darstellt, wie viel oder wie viele von einer Sache pro Flächeneinheit vorhanden sind. Das Dichte-Werkzeug ist nützlich, um Dichteflächen zu erstellen, die die Verteilung einer Wildtierpopulation anhand einer Reihe von Beobachtungen oder den Grad der Verstädterung eines Gebiets anhand der Straßendichte darstellen.

Density Raster; Courtest: ERSI
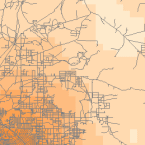
Density and Roads; Courtesy: ESRI
There are density tools for point and line features in ArcGIS.
Related Topics
- What is Interpolation ?
- Classification of Interpolation Techniques.
- Choosing the Right Interpolation Method