dB: Was ist ein Dezibel?

Schalldruck, Schallpegel und dB. Schall wird in der Regel mit Mikrofonen gemessen, und diese reagieren proportional zum Schalldruck p. Die Leistung einer Schallwelle verhält sich also zum Quadrat des Drucks. (Ähnlich verhält es sich mit der elektrischen Leistung in einem Widerstand, die mit dem Quadrat der Spannung zunimmt). Der Logarithmus von x2 ist einfach 2 log x, so dass bei der Umrechnung von Druckverhältnissen in Dezibel ein Faktor von 2 hinzukommt. Der Unterschied im Schalldruckpegel zwischen zwei Tönen mit p1 und p2 ist also:

20 log (p2/p1) dB = 10 log (p22/p12) dB = 10 log (P2/P1) dB (der Logarithmus ist immer zur Basis 10).

Was passiert, wenn man die Schallleistung halbiert? Der Logarithmus von 2 ist 0,3010, also ist der Logarithmus von 1/2 in guter Näherung -0,3. Wenn Sie also die Leistung halbieren, verringern Sie die Leistung und den Schallpegel um 3 dB. Halbiert man die Leistung erneut (auf 1/4 der ursprünglichen Leistung), verringert sich der Pegel um weitere 3 dB. Wenn man die Leistung weiter halbiert, erhält man diese Verhältnisse.

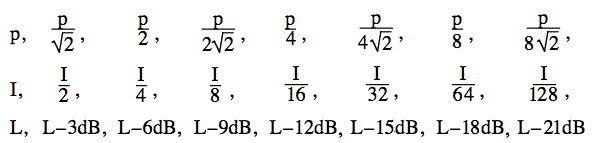
Was passiert, wenn ich zwei identische Töne hinzufüge? Verdopple ich die Intensität (Erhöhung um 3 dB)? Oder verdopple ich den Druck (Erhöhung um 6 dB)? Diese häufig gestellte Frage ist ein wenig heikel, deshalb wird sie hier in unseren FAQ behandelt.

Tondateien zur Veranschaulichung der Größe eines Dezibel

Wir haben oben gesehen, dass eine Halbierung der Leistung den Schalldruck um √2 und den Schallpegel um 3 dB verringert. Das haben wir in der ersten Grafik und der folgenden Tondatei getan.

Das erste Klangbeispiel ist weißes Rauschen (eine Mischung aus einem breiten Spektrum hörbarer Frequenzen, analog zu weißem Licht, das eine Mischung aus allen sichtbaren Frequenzen ist). Die zweite Probe ist das gleiche Rauschen, wobei die Spannung um den Faktor √2 reduziert ist. Nun ist 1/√2 ungefähr 0,7, so dass -3 dB einer Verringerung der Spannung oder des Drucks auf 70 % des ursprünglichen Wertes entspricht. Die grüne Linie zeigt die Spannung als eine Funktion der Zeit. Die rote Linie zeigt einen kontinuierlichen exponentiellen Abfall mit der Zeit. Man beachte, dass die Spannung bei jeder zweiten Probe um 50 % abfällt. Beachten Sie auch, dass eine Verdoppelung der Leistung keinen großen Unterschied in der Lautstärke macht. Wir werden dies weiter unten besprechen, aber es ist ein nützlicher Hinweis bei der Auswahl von Tonwiedergabegeräten. Tondateien und Animation von John Tann und George Hatsidimitris.

Wie groß ist ein Dezibel? In der nächsten Serie werden die aufeinanderfolgenden Proben um nur ein Dezibel verringert.

Ein Dezibel liegt in der gleichen Größenordnung wie die Just Noticeable Difference (JND) für den Schallpegel. Wenn Sie sich diese Dateien anhören, werden Sie feststellen, dass die letzte leiser ist als die erste, aber es ist für das Ohr weniger klar, dass die zweite eines Paares leiser ist als ihre Vorgängerin. 10*log10(1,26) = 1. Um den Schallpegel um 1 dB zu erhöhen, muss also die Leistung um 26 % oder die Spannung um 12 % erhöht werden.

Was, wenn der Unterschied weniger als ein Dezibel beträgt? Schallpegel werden selten mit Dezimalstellen angegeben. Der Grund dafür ist, dass Schallpegel, die sich um weniger als 1 dB unterscheiden, schwer zu unterscheiden sind, wie das nächste Beispiel zeigt.(Das macht das dB zu einer praktischen Größeneinheit.)

0,3 dB Schritte. Sie können feststellen, dass das letzte Paar leiser ist als das erste, aber es ist schwierig, den Unterschied zwischen aufeinanderfolgenden Paaren zu erkennen. 10*log10(1,07) = 0,3, um also den Schallpegel um 0,3 dB zu erhöhen, muss die Leistung um 7% oder die Spannung um 3,5% erhöht werden.

Standard-Referenzpegel („absoluter“ Schallpegel)

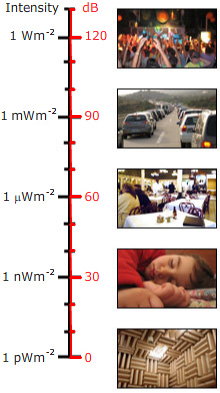Wir haben oben gesagt, dass das Dezibel ein Verhältnis ist. Wenn er also zur Angabe des Schallpegels für ein einzelnes Geräusch und nicht als Verhältniszahl verwendet wird, muss ein Referenzpegel gewählt werden. Für den Schalldruckpegel wird der Bezugswert (für Luft) gewöhnlich mit pref = 20 Mikropascal (20 μPa) oder 0,02 mPa gewählt. Dies ist ein sehr niedriger Wert: Er entspricht 2 Zehnmilliardstel einer Atmosphäre. Dennoch ist dies ungefähr die Grenze der Empfindlichkeit des menschlichen Ohrs in seinem empfindlichen Frequenzbereich. (Normalerweise ist diese Empfindlichkeit nur bei sehr jungen Menschen oder bei Menschen, die noch nicht mit lauter Musik oder anderen lauten Geräuschen in Berührung gekommen sind, gegeben. Persönliche Musiksysteme mit In-Ear-Lautsprechern sind in der Lage, sehr hohe Schallpegel im Ohr zu erzeugen, und werden von einigen für einen Großteil der Hörverluste bei jungen Erwachsenen in einigen Ländern verantwortlich gemacht.)

Wenn man also von einem Schalldruckpegel von 86 dB liest, bedeutet das:

20 log (p2/pref) = 86 dB

wobei pref der Schalldruck des Referenzpegels ist und p2 der des fraglichen Schalls. Dividieren Sie beide Seiten durch 20:

log (p2/pref) = 4,3

p2/pref = 104,3

4 ist der Logarithmus von 10 Tausend, 0,3 ist der Logarithmus von 2, also hat dieser Schall einen Schalldruck, der 20 Tausend Mal höher ist als der des Referenzpegels (p2/pref = 20.000) oder eine Intensität, die 400 Millionen Mal höher ist als die des Referenzpegels. 86 dB ist ein lautes Geräusch, aber nicht gefährlich – vorausgesetzt, die Einwirkung ist kurz.

Was bedeutet 0 dB? Dieser Pegel tritt auf, wenn die gemessene Intensität gleich dem Referenzpegel ist, d. h. es ist der Schallpegel, der 0,02 mPa entspricht. In diesem Fall haben wir

Schallpegel = 20 log (pmeasured/pref) = 20 log 1 = 0 dB

Denken Sie daran, dass Dezibel ein Verhältnis messen. 0 dB entsteht, wenn man den Logarithmus eines Verhältnisses von 1 nimmt (log 1 = 0). 0 dB bedeutet also nicht, dass es keinen Schall gibt, sondern einen Schallpegel, bei dem der Schalldruck gleich dem des Referenzpegels ist. Dies ist ein geringer Druck, aber nicht Null. Es sind auch negative Schallpegel möglich: – 20 dB würde einen Schall bedeuten, dessen Druck 10-mal kleiner ist als der Referenzdruck, also 2 μPa.

Nicht alle Schalldrücke sind gleich laut. Das liegt daran, dass das menschliche Ohr nicht auf alle Frequenzen gleichermaßen reagiert: Wir sind viel empfindlicher für Töne im Frequenzbereich von etwa 1 kHz bis 7 kHz (1000 bis 7000 Schwingungen pro Sekunde) als für sehr tiefe oder hohe Frequenzen. Aus diesem Grund sind Schallmessgeräte in der Regel mit einem Filter ausgestattet, dessen Frequenzgang in etwa dem des menschlichen Ohrs entspricht. (Mehr zu diesen Filtern weiter unten.) Wenn der „A-Bewertungsfilter“ verwendet wird, wird der Schalldruckpegel in dB(A) oder dBA angegeben. Der Schalldruckpegel auf der dBA-Skala ist leicht zu messen und wird daher häufig verwendet. Ein Grund, warum er sich von der Lautheit unterscheidet, ist, dass der Filter nicht auf die gleiche Weise reagiert wie das Ohr. Um die Lautstärke eines Geräuschs zu verstehen, müssen Sie zunächst einige Kurven nachschlagen, die den Frequenzgang des menschlichen Ohrs darstellen (siehe unten). (Ein weiterer Grund ist, dass das menschliche Gehör nicht logarithmisch ist.

Logarithmische Maße

Warum verwenden wir Dezibel? Das Ohr ist in der Lage, einen sehr großen Bereich von Tönen zu hören: Das Verhältnis zwischen dem Schalldruck, der bei kurzer Einwirkung bleibende Schäden verursacht, und dem Grenzwert, den (unbeschädigte) Ohren hören können, beträgt mehr als eine Million. Um mit einem solchen Bereich umzugehen, sind logarithmische Einheiten nützlich: der Logarithmus von einer Million ist 6, also entspricht dieses Verhältnis einem Unterschied von 120 dB. Das Gehör reagiert jedoch nicht von Natur aus logarithmisch. (Logarithmische Maße sind auch nützlich, wenn ein Geräusch (kurz) exponentiell über die Zeit ansteigt oder abfällt. Dies ist bei vielen Anwendungen der Fall, die eine proportionale Verstärkung oder einen proportionalen Verlust beinhalten.)

Die für dBA und dB(C)

Der am häufigsten verwendete Schallpegelfilter ist die A-Skala, die in etwa der Umkehrung der 40-dB-Lautstärkekurve (bei 1 kHz) entspricht. Mit diesem Filter ist der Schallpegelmesser weniger empfindlich gegenüber sehr hohen und sehr tiefen Frequenzen. Die Messungen auf dieser Skala werden in dBA angegeben. Die C-Skala variiert über mehrere Oktaven nur wenig und eignet sich daher für subjektive Messungen nur bei mittleren bis hohen Schallpegeln. Messungen auf dieser Skala werden in dB(C) ausgedrückt. Es gibt auch eine (selten verwendete) Bewertungsskala B, die zwischen A und C liegt. Die folgende Abbildung zeigt die Reaktion des A-Filters (links) und des C-Filters, wobei die Verstärkungen in dB in Bezug auf 1 kHz angegeben sind. (Für eine Einführung in die Filter siehe RC-Filter, Integratoren und Differenzierer).



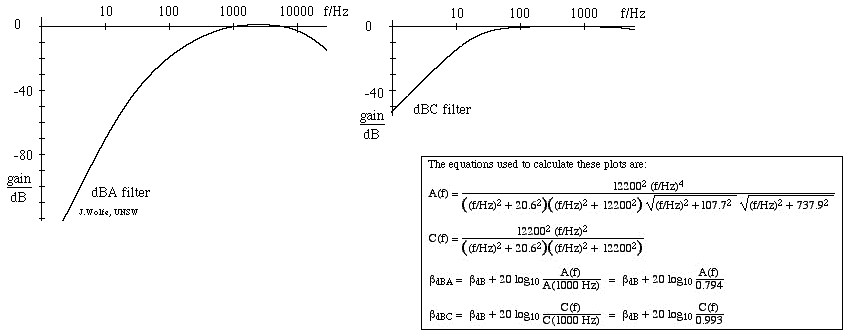
Auf den Seiten zur Musikakustik und zur Sprachakustik werden die Schallspektren in dB angegeben. Der Grund für diese gängige Praxis ist, dass der Bereich der gemessenen Schalldrücke groß ist.

Die dB(G)-Messungen verwenden einen Schmalbandfilter, der die Frequenzen zwischen 1 und 20 Hz hoch und die anderen niedrig gewichtet. Dadurch ergeben sich hohe Werte für Geräusche und Infraschall, die nicht ohne weiteres gehört werden können. ISO 7196:1995

Lautheit, Phon und Sones, Hörkurven

Das Phon ist eine Einheit, die durch den psychophysikalisch gemessenen Frequenzgang des Ohres auf dB bezogen wird. Bei 1 kHz sind die Angaben in phon und dB per Definition gleich. Für alle anderen Frequenzen wird die Phon-Skala durch die Ergebnisse von Experimenten bestimmt, bei denen Freiwillige aufgefordert wurden, die Lautstärke eines Signals bei einer bestimmten Frequenz so einzustellen, dass sie die Lautstärke eines 1-kHz-Signals als gleich empfanden. Um von dB in Phon umzurechnen, benötigt man eine grafische Darstellung dieser Ergebnisse. Ein solches Diagramm hängt vom Schallpegel ab: Bei hohen Schallpegeln wird es flacher.

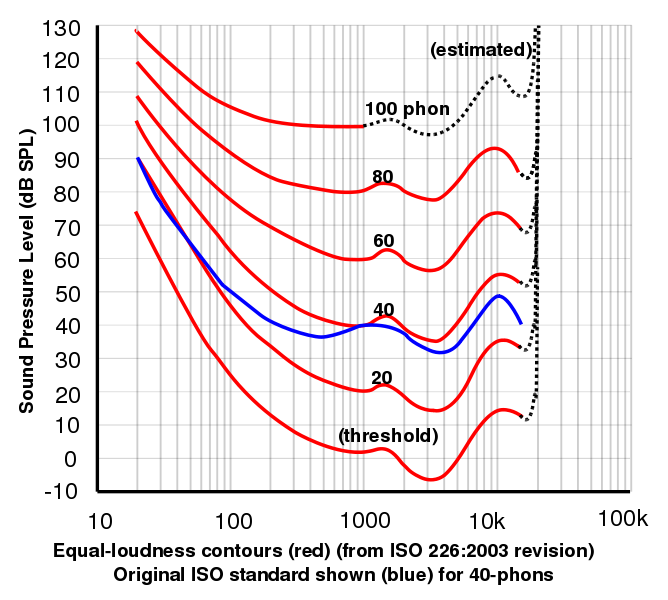
Dieses Diagramm, das freundlicherweise von Lindosland zur Verfügung gestellt wurde, zeigt die 2003 von der International Standards Organisation ermittelten Kurven gleicher Lautheit. Kurven gleicher Lautheit in Abhängigkeit von der Frequenz werden oft als Fletcher-Munson-Kurven bezeichnet, nach der ursprünglichen Arbeit von Fletcher, H. und Munson, W.A. (1933) J.Acoust.Soc.Am. 6:59. Sie können Ihre eigenen Kurven auf unserer Website für Hörreaktionen erstellen.

Der Sone wurde aus psychophysikalischen Messungen abgeleitet, bei denen Freiwillige Geräusche so einstellen, dass sie sie als doppelt so laut empfinden. Auf diese Weise kann man die wahrgenommene Lautstärke mit Phon in Beziehung setzen. Ein Sone ist definiert als 40 Phon. Experimentell wurde festgestellt, dass eine Erhöhung des Schallpegels um 10 dB oberhalb von 40 Phon ungefähr einer empfundenen Verdopplung der Lautstärke entspricht. Dieser Näherungswert wird daher bei der Definition des Sone verwendet: 1 Sone = 40 Phon, 2 Sone = 50 Phon, 4 Sone = 60 Phon usw.



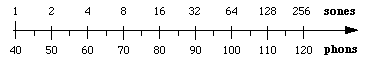
Dieser Zusammenhang impliziert, dass Lautheit und Intensität durch ein Potenzgesetz miteinander verbunden sind: Lautheit in Sone ist proportional zu (Intensität)log 2 = (Intensität)0,3.

Wäre es nicht großartig, wenn man von dB (die mit einem Instrument gemessen werden können) in Sone umrechnen könnte (was der von Menschen wahrgenommenen Lautstärke entspricht)? Dies geschieht manchmal mit Hilfe von Tabellen, die man in Akustik-Handbüchern finden kann. Wenn Sie jedoch nichts gegen eine recht grobe Annäherung einzuwenden haben, können Sie sagen, dass die A-Bewertungskurve den menschlichen Frequenzgang bei niedrigen bis mittleren Schallpegeln annähert, so dass dB(A) über einen begrenzten Bereich niedriger Pegel in etwa dasselbe ist wie Phon. Dann kann man die oben beschriebene logarithmische Beziehung zwischen sones und phons verwenden.

Aufnahmepegel und Dezibel

Messgeräte, die den Aufnahme- oder Ausgangspegel an elektronischen Audiogeräten (Mischpulten usw.) messen, zeichnen fast immer die Effektivwechselspannung auf (siehe Links, um mehr über AC und Effektivwert zu erfahren). Für einen gegebenen Widerstand R ist die Leistung P gleich V2/R, also
Spannungspegelunterschied = 20 log (V2/V1) dB = 10 log (V22/V12) dB = 10 log (P2/P1) dB, oder

absoluter Spannungspegel = 20 log (V/Vref)

wobei Vref eine Referenzspannung ist. Was ist also die Referenzspannung?

Der naheliegende Pegel ist ein Volt rms, und in diesem Fall wird der Pegel als dBV geschrieben. Das ist rationell und auch praktisch bei Analog-Digital-Karten, deren maximaler Bereich oft bei einem Volt rms liegt. Man muss also daran denken, den Pegel in negativen dBV (weniger als ein Volt) zu halten, um die Spitzen des Signals nicht zu beschneiden, aber nicht zu negativ (so dass das Signal immer noch viel größer ist als das Hintergrundrauschen).

Gelegentlich wird auch die Angabe dBm verwendet. Dies bedeutete früher Dezibel elektrischer Leistung, bezogen auf ein Milliwatt, und manchmal ist es immer noch so. Aus historischen Gründen ist es jedoch kompliziert. Jahrhunderts hatten viele Audioleitungen eine Nennimpedanz von 600 Ω. Wenn die Impedanz rein ohmsch ist und Sie V2/600 Ω = 1 mW setzen, erhalten Sie V = 0,775 Volt. Unter der Voraussetzung, dass Sie eine 600 Ω-Last verwenden, entspricht 1 mW Leistung 0 dBm, also 0,775 V, und Sie haben Ihre Pegelmesser entsprechend kalibriert. Das Problem bestand darin, dass ein Pegelmesser, der Spannung misst, wenn er einmal so kalibriert ist, 0 dBm bei 0,775 V anzeigt, auch wenn er nicht an 600 Ω angeschlossen ist. Daher bedeutet dBm manchmal – vielleicht unlogischerweise – dB in Bezug auf 0,775 V. (Als ich ein Junge war, waren Taschenrechner teuer, also benutzte ich Papas alten Rechenschieber, der den Faktor 0,775 auf dem Cursorfenster markiert hatte, um solche Berechnungen zu erleichtern).

Wie konvertiert man dBV oder dBm in dB des Schallpegels? Es gibt keinen einfachen Weg. Es kommt darauf an, wie man die elektrische Leistung in Schallleistung umwandelt. Selbst wenn Ihr elektrisches Signal direkt an einen Lautsprecher angeschlossen ist, hängt die Umwandlung vom Wirkungsgrad und der Impedanz Ihres Lautsprechers ab. Und natürlich kann es einen Leistungsverstärker und verschiedene akustische Komplikationen zwischen dem Ort, an dem Sie den dBV-Wert am Mischpult messen, und dem Ort, an dem sich Ihre Ohren im Schallfeld befinden, geben.

Intensität, Strahlung und dB

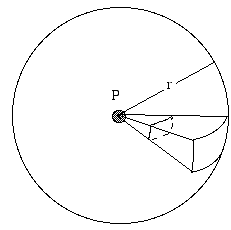
Wie hängt der Schallpegel (oder der Pegel eines Radiosignals usw.) vom Abstand zur Quelle ab?

Eine Quelle, die in alle Richtungen gleichmäßig abstrahlt, nennt man isotrop. Stellen Sie sich eine isolierte Schallquelle vor, die weit von reflektierenden Oberflächen entfernt ist – vielleicht ein Vogel, der hoch in der Luft singt. Stellen Sie sich eine Kugel mit dem Radius r vor, deren Mittelpunkt die Quelle ist. Die Quelle gibt kontinuierlich eine Gesamtleistung P ab. Diese Schallleistung breitet sich aus und durchdringt die Oberfläche der Kugel. Wenn die Quelle isotrop ist, ist die Intensität I per Definition überall auf dieser Oberfläche gleich. Die Intensität I ist definiert als die Leistung pro Flächeneinheit. Die Oberfläche der Kugel ist 4πr2, also ist die Leistung (in unserem Beispiel die Schallleistung), die durch jeden Quadratmeter der Oberfläche geht, per Definition:

I = P/4πr2.

Wir sehen also, dass für eine isotrope Quelle die Intensität umgekehrt proportional zum Quadrat des Abstands von der Quelle ist:

I2/I1 = r12/r22.

Die Intensität ist aber proportional zum Quadrat des Schalldrucks, so dass wir auch schreiben könnten:

p2/p1 = r1/r2.

Wenn wir also den Abstand verdoppeln, verringern wir den Schalldruck um den Faktor 2 und die Intensität um den Faktor 4: Mit anderen Worten, wir verringern den Schallpegel um 6 dB. Wenn wir r um den Faktor 10 erhöhen, verringern wir den Pegel um 20 dB usw.

Allerdings ist zu beachten, dass viele Quellen nicht isotrop sind, vor allem wenn die Wellenlänge kleiner ist als die Quelle oder eine vergleichbare Größe hat. Außerdem spielen Reflexionen oft eine große Rolle, vor allem, wenn der Boden in der Nähe ist oder man sich in geschlossenen Räumen befindet.

Druck, Intensität und spezifische Impedanz

Für akustische Wellen ist die spezifische akustische Impedanz z definiert als das Verhältnis zwischen dem Schalldruck p und der mittleren Teilchengeschwindigkeit u, bedingt durch die Schallwelle, z = p/u . In Akustische Impedanz, Intensität und Leistung zeigen wir, wie man den RMS-Schalldruck p und die Intensität I in Beziehung setzt:
I = p2/z

Für Luft beträgt die spezifische akustische Impedanz z 420 kg.s-1.m-2 = 420 Pa.s.m-1. Für (Süß-)Wasser beträgt die spezifische akustische Impedanz für Wasser 1,48 MPa.s.m-1. Eine Schallwelle in Wasser hat also bei gleichem Druck eine viel geringere Intensität als eine in Luft.

dBi und richtungsabhängige Strahlung

Strahlung, die in der Richtung variiert, wird anisotrop genannt. In vielen Fällen der Kommunikation ist isotrope Strahlung verschwenderisch: Warum sollte man einen beträchtlichen Teil der Leistung nach oben abstrahlen, wenn sich der Empfänger, wie Sie, relativ nahe am Boden befindet. Bei Schall mit kurzer Wellenlänge (einschließlich der meisten für die Sprache wichtigen Bereiche) kann ein Megaphon dazu beitragen, dass Ihre Stimme anisotroper wird. Beim Radio gibt es eine breite Palette von Antennen, die sowohl für die Übertragung als auch für den Empfang eine hohe Anisotropie aufweisen.

Wenn Sie also an der Abstrahlung in eine bestimmte Richtung (oder am Empfang aus einer bestimmten Richtung) interessiert sind, möchten Sie, dass das Verhältnis der in dieser Richtung gemessenen Intensität in einer bestimmten Entfernung höher ist als das Verhältnis, das in der gleichen Entfernung von einem isotropen Strahler gemessen (oder von einem isotropen Empfänger empfangen) wird. Dieses Verhältnis wird als Gewinn bezeichnet; drückt man das Verhältnis in dB aus, erhält man den Gewinn in dBi für diesen Strahler. Diese Einheit wird hauptsächlich für Antennen verwendet, sowohl beim Senden als auch beim Empfangen, aber manchmal auch für Schallquellen und Richtmikrofone.

Beispielprobleme

Ein paar Leute haben geschrieben und nach Beispielen für die Verwendung von dB in Berechnungen gefragt. Also…
• Wie viel lauter wird ein Lautsprecher (in seinem linearen Bereich) von einem 100-W-Verstärker angetrieben als von einem 10-W-Verstärker, wenn alles andere gleich bleibt?

  Die Leistungen unterscheiden sich um den Faktor zehn, was, wie wir oben gesehen haben, 10 dB entspricht. Alles andere ist gleich, d.h. die Frequenzgänge sind gleich, es wird das gleiche Eingangssignal verwendet, usw. Die Frequenzabhängigkeit sollte also die gleiche sein. 10 dB entsprechen 10 Phon. Um eine wahrgenommene Verdoppelung der Lautstärke zu erreichen, ist eine Zunahme von 10 Phon erforderlich. Der vom 100-W-Verstärker angesteuerte Lautsprecher ist also doppelt so laut wie der vom 10-W-Verstärker angesteuerte, vorausgesetzt, Sie bleiben im linearen Bereich und verzerren oder zerstören den Lautsprecher nicht. (Der 100-W-Verstärker erzeugt doppelt so viele Töne wie der 10-W-Verstärker.)

• Ich stehe in einem Abstand R von einer kleinen Schallquelle (Größe viel kleiner als R), auf Bodenhöhe im Freien, wo Reflexionen vernachlässigt werden können. Der Schallpegel ist L. Wenn ich mich nun in eine Entfernung nR bewege (n eine Zahl, und nR immer noch viel größer als die Größe der Schallquelle), wie hoch ist dann der neue Schallpegel?

  Zunächst ist zu beachten, dass die Vernachlässigung von Reflexionen sehr wichtig ist. Diese Berechnung wird in einem Raum nicht funktionieren, da die Reflexionen an den Wänden (die zusammen einen Nachhall erzeugen) die Berechnung ziemlich schwierig machen. Im Freien ist die Schallintensität proportional zu 1/r2, wobei r die Entfernung von der Schallquelle ist. (Die Proportionalitätskonstante hängt davon ab, wie gut der Boden reflektiert, und ist hier nicht von Belang, da sie sich bei der Berechnung in etwa aufhebt, vorausgesetzt, r ist einigermaßen groß.) Wenn wir also r von R auf nR erhöhen, verringern wir die Intensität von I auf I/n 2.

  Der Unterschied in Dezibel zwischen den beiden Signalen der Intensität I 2 und I 1 ist oben definiert als

  ΔL = 10 log (I2/I1) = 10 log ((I/n 2)/I) = 10 log (1/n 2) = -10 log (n 2) = -20 log n.

  Wenn n zum Beispiel 2 ist (d.h. wenn wir doppelt so weit weg gehen), wird die Intensität um den Faktor 4 reduziert und der Schallpegel fällt von L auf (L – 6dB).

• Wenn ein Jugendlicher unter idealen, ruhigen Bedingungen einen 1-kHz-Ton mit 0 dB hören kann, der von einem Lautsprecher (vielleicht einem Softspeaker?) ausgestrahlt wird, um wie viel muss die Leistung des Lautsprechers erhöht werden, um den Schall auf 110 dB zu erhöhen (ein gefährlich lauter, aber erträglicher Pegel)?

  Der Unterschied in Dezibel zwischen den beiden Signalen der Leistung P2 und P1 ist oben definiert als

  ΔL = 10 log (P2/P1) dB, also 10 hoch die Potenz dieser beiden gleichen Größen:
  10L/10 = P2/P1 also:
  P2/P1 = 10110/10 = 1011 = hunderttausend Millionen.

  Dies zeigt, dass das menschliche Ohr einen bemerkenswert großen Dynamikbereich hat, der vielleicht größer ist als der des Auges.

• Ein Verstärker hat einen Eingang von 10 mV und einen Ausgang von 2 V. Wie hoch ist seine Spannungsverstärkung in dB?

  Die Spannung erscheint, wie der Druck, im Quadrat in Ausdrücken für Leistung oder Intensität. (Die in einem Widerstand R abgeleitete Leistung ist V2/R.) Wir definieren also per Konvention:

  Verstärkung = 20 log (Vout/Vin)
  = 20 log (2V/10mV)
  = 46 dB

  (In den oben genannten akustischen Fällen haben wir gesehen, dass das Druckverhältnis, ausgedrückt in dB, dasselbe ist wie das Leistungsverhältnis: Das war der Grund für den Faktor 20 bei der Definition von dB für Druck. Es sei darauf hingewiesen, dass im Beispiel der Spannungsverstärkung die Leistungsverstärkung des Verstärkers wahrscheinlich nicht gleich der Spannungsverstärkung ist, die durch die hier verwendete Konvention definiert ist. Die Leistung ist proportional zum Quadrat der Spannung an einem bestimmten Widerstand. Die Eingangs- und Ausgangsimpedanzen von Verstärkern sind jedoch oft recht unterschiedlich. Ein Pufferverstärker oder Emitterfolger hat zum Beispiel eine Spannungsverstärkung von etwa 1, aber eine große Stromverstärkung).

• Wie groß ist der Unterschied in dB zwischen der Bestrahlungsstärke (Lichtintensität) auf der Erde (8,3 Lichtminuten von der Sonne entfernt) und auf dem Uranus (160 Lichtminuten)?

  Wie der Schall nimmt auch die isotrope Lichtintensität mit r-2 ab, das Intensitätsverhältnis ist also (160/8.3)2 = 20 log (160/8.3) = 26 dB.

Arbeitsschutz

Natürlich gibt es in verschiedenen Ländern und Provinzen unterschiedliche Gesetze zur Lärmbelastung am Arbeitsplatz, die mit unterschiedlichem Eifer durchgesetzt werden. Viele dieser Vorschriften sehen einen Grenzwert für die Belastung durch Dauerlärm von 85 dB(A) für eine 8-Stunden-Schicht vor. Für jede Erhöhung um 3 dB halbiert sich die zulässige Belastung. Wenn Sie also in einem Nachtclub arbeiten, in dem verstärkte Musik in Ohrnähe 100 dB(A) erzeugt, dürfen Sie sich nur 15 Minuten lang dem Lärm aussetzen. Es gibt einen Grenzwert für Impulslärm wie Schusswaffen oder Werkzeuge, die explosive Schüsse abgeben. (z. B. sollte ein Spitzenwert von 140 dB zu keinem Zeitpunkt des Tages überschritten werden.) Es gibt zahlreiche Dokumente, die Ratschläge zur Verringerung der Lärmbelastung an der Quelle (z. B. die Musik leiser stellen), zwischen der Quelle und dem Ohr (z. B. sich bei einem Konzert von den Lautsprechern entfernen) und am Ohr (z. B. Ohrstöpsel oder Gehörschutz tragen) geben. Lärmmanagement und Gehörschutz am Arbeitsplatz ist das Regelwerk im Bundesstaat New South Wales, Australien (Adresse des Autors).

Einige FAQs

• Wie laut ist ein Flugzeug? Ein Zug? Ein Mensch, der singt? Ein bellender Hund? Ein Elektrowerkzeug? Die Antworten auf diese Frage sind sehr unterschiedlich. Sie hängt stark davon ab, wie weit Sie entfernt sind, ob Sie sich in einem Raum befinden oder nicht, ob es einen Nachhall gibt, wie stark die jeweilige Quelle ist und welches Spektrum sie hat. Es wäre etwas irreführend, Werte zu nennen, ohne die Bedingungen genau zu beschreiben. Da der Rest dieser Seite, soweit es geht, zuverlässig sein soll, möchte ich hier lieber keine Werte angeben.
• Wie kann man „Dezibel addieren“, d.h. welchen Schallpegel erhält man, wenn man Pegel a zu Pegel b addiert? Wenn die Quellen kohärent sind (was in der Regel bedeutet, dass sie letztlich aus derselben Quelle stammen), dann kann es zu komplizierten Interferenzeffekten kommen. In den meisten Fällen, in denen die Quellen unabhängig sind, kann man die Intensitäten addieren und dann in Dezibel umrechnen. Wenn man jedoch die Schallpegel in dB(A) erhält, ist es nicht so einfach, auf die Intensität zurückzurechnen, und man muss etwas über das Spektrum des Schalls wissen. Wenn du die Verteilung des Schalls in verschiedenen Frequenzbändern kennst, kannst du das Applet unter diesem Link verwenden.
• Some of the questions on our FAQ in music acoustics relate to decibels, including
  • Why do the sounds of two musical instruments always reinforce, and never cancel out?
  • How much does one more violin add to the sound level of a section of n violins?
  • Does adding two equal sounds give an increase of 3 or 6 dB? Why?
  • What is the loudest sound?
  • Is there really no sound in space?

Related pages

• Measure your own hearing response
• Adding sound levels from incoherent sources
• What are interference beats and Tartini tones?
• FAQ in music acoustics
• Loudness and spectra: how spectral content and other features are related to loudness
• Formants: what are they? A discussion of the different meanings of this term
• Music acoustics home page
• Physclips: a multi-level, multimedia introduction to mechanics.
• A list of other educational web sites from this author.