Marginalverteilung

Wahrscheinlichkeitsverteilungen > Marginalverteilung

Was ist eine Marginalverteilung?

Schauen Sie sich das Video an oder lesen Sie den Artikel unten:

Die technische Definition kann etwas verwirrend sein:

Definition einer Randverteilung = Wenn X und Y diskrete Zufallsvariablen sind und f (x,y) der Wert
ihrer gemeinsamen Wahrscheinlichkeitsverteilung bei (x,y) ist, sind die Funktionen gegeben durch:
g(x) = Σy f (x,y) und h(y) = Σx f (x,y) sind die Randverteilungen von X bzw. Y.

Wenn du dich mit Gleichungen auskennst, ist das wahrscheinlich alles, was du wissen musst. Sie sagt Ihnen, wie Sie eine Randverteilung finden können. Aber wenn dir diese Formel Kopfschmerzen bereitet (was bei den meisten Leuten der Fall ist!), kannst du eine Häufigkeitsverteilungstabelle verwenden, um eine Randverteilung zu finden.

Eine Randverteilung hat ihren Namen, weil sie am Rand einer Wahrscheinlichkeitsverteilungstabelle erscheint.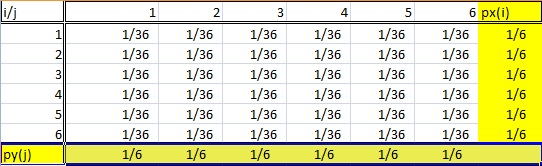

Natürlich ist es nicht ganz so einfach. Man kann nicht einfach irgendeine alte Häufigkeitsverteilungstabelle betrachten und sagen, dass die letzte Spalte (oder Zeile) eine „Randverteilung“ ist. Marginalverteilungen folgen einer Reihe von Regeln:

• Die Verteilung muss aus bivariaten Daten stammen. Bivariat ist nur eine andere Bezeichnung für „zwei Variablen“, wie X und Y. In der obigen Tabelle stammen die Zufallsvariablen i und j aus dem Wurf von zwei Würfeln.
• Eine Randverteilung liegt vor, wenn man nur an einer der Zufallsvariablen interessiert ist. Mit anderen Worten, entweder X oder Y. In der obigen Wahrscheinlichkeitstabelle sind die Summenwahrscheinlichkeiten einer Variablen in der unteren Zeile und die anderen Summenwahrscheinlichkeiten in der rechten Spalte aufgeführt. Diese Tabelle hat also zwei Randverteilungen.

Unterschied zwischen Randverteilung und bedingter Verteilung.

Bei einer bedingten Verteilung sind wir nur an einer bestimmten Teilpopulation unseres gesamten Datensatzes interessiert. Im Beispiel des Würfelwurfs könnte dies „eine Zwei würfeln“ oder „eine Sechs würfeln“ sein. Die folgende Abbildung zeigt zwei hervorgehobene Teilpopulationen (und damit zwei bedingte Verteilungen).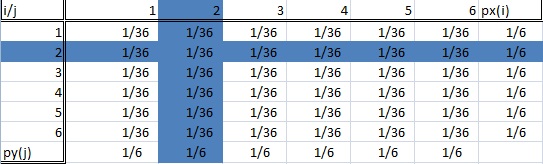

Wie man die Grenzverteilung der Wahrscheinlichkeit berechnet

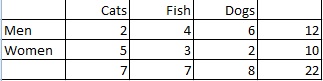
Beispielfrage: Berechnen Sie die Randverteilung der Tierpräferenz bei Männern und Frauen:
Lösung:
Schritt 1: Zählen Sie die Gesamtzahl der Personen. In diesem Fall ist die Gesamtzahl in der rechten Spalte angegeben (22 Personen).
Schritt 2: Zähle die Anzahl der Personen, die jede Haustierart bevorzugen, und wandle dann das Verhältnis in eine Wahrscheinlichkeit um:
Personen, die Katzen bevorzugen: 7/22 = .32
Personen, die Fische bevorzugen: 7/22 = .32
Personen, die Hunde bevorzugen: 8/22 = .36
Tipp: Du kannst deine Antwort überprüfen, indem du sicherstellst, dass die Wahrscheinlichkeiten sich alle zu 1 addieren.

Beispielfrage 2 (sich gegenseitig ausschließende Ereignisse): Wenn P(A) = 0,20, P(b) = 0,70, und beide Ereignisse sich gegenseitig ausschließen, finden Sie P(B’∩A), P(B’∩A‘) und P(B∩A‘).
Wenn Sie mit dieser Schreibweise nicht vertraut sind, bedeutet P(A‘) „nicht A“ oder das Komplement. P(B’∩A) bedeutet „die Schnittmenge von nicht B und A“).

Antwort:
Sie könnten die Wahrscheinlichkeiten einzeln ausrechnen, aber es ist viel einfacher, sie anhand einer Tabelle zu ermitteln.

Schritt 1: Füllen Sie eine Häufigkeitstabelle mit den gegebenen Informationen aus. Die Gesamtwahrscheinlichkeit muss gleich 1 sein, also kannst du sie auch zu den Rändern (Summen) addieren. Einfache Addition/Algebra füllt die Randbereiche aus. Beispiel: In der untersten Zeile 0,70 + x = 1,00. Die Randsumme für B‘ muss also 0,30 betragen.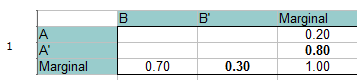

Schritt 2: Füge 0 für den Schnittpunkt von A und B hinzu, oben links in der Tabelle. Das geht, weil A und B sich gegenseitig ausschließen und nicht zusammen vorkommen können.

Schritt 3: Füllen Sie die restlichen Lücken mit einfacher Addition/Algebra aus.

Lesen Sie aus der Tabelle (betrachten Sie die Schnittpunkte der beiden angegebenen Wahrscheinlichkeiten):
P(B’∩A) = 0,20
P(B’∩A‘) = 0,10
P(B∩A‘) = 0,70.

Beispielfrage 3 (Unabhängige Ereignisse): Wenn P(A) = 0,20, P(b) = 0,70, und beide Ereignisse unabhängig sind, finden Sie P(B’∩A), P(B’∩A‘) und P(B∩A‘).

Antwort: Diesmal sind A und B unabhängig voneinander, so dass die Wahrscheinlichkeit, dass sie beide gleichzeitig eintreten, 0,14 beträgt (P(A)*P(B) = 0,20 * 0,70 = 0,14). Dieser Wert wird oben links eingetragen (Schnittpunkt von A und B). Füllen Sie den Rest der Tabelle genauso aus wie in den obigen Schritten.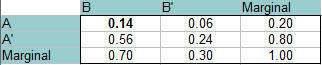

Lesen Sie die Antworten aus der Tabelle (aus den Schnittpunkten der beiden Wahrscheinlichkeiten):
P(B’∩A): 0.06
P(B’∩A‘): 0.24
P(B∩A‘): 0.56.

Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, S. 536 und 571, 2002.
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education

——————————————————————————

Brauchen Sie Hilfe bei einer Hausaufgabe oder einer Prüfungsfrage? Mit Chegg Study erhalten Sie Schritt-für-Schritt-Lösungen zu Ihren Fragen von einem Experten auf diesem Gebiet. Die ersten 30 Minuten mit einem Chegg-Lehrer sind kostenlos!