Solving the Königsberg Bridge Problem
This proof is accessible to ANYONE — no mathematics knowledge required! (perfect for if you are a bit bored and in isolation, like me right now!)
The Königsberg bridge problem shows the beauty of mathematics to transform the impossible to the obvious. It also gives an insight into the mind of the genius Leonhard Euler.

Stating the problem
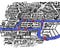
Have a look at the map above.
It’s a diagram of the rivers and bridges of Königsberg. The areas A, B, C and D are bits of land, joined by the bridges, but otherwise cut off from each other by water.
A map of the city is below. Sie können sich beide Diagramme ansehen – beide erfassen die wichtigsten Informationen: welche Landstücke mit welchen anderen Landstücken verbunden sind und durch wie viele Brücken.
Im Fachjargon stellen wir dies als Diagramm dar. Die Landstücke sind die Eckpunkte, und die Brücken sind die Kanten. Aber das ist nicht wichtig.
Das Problem ist, ob es möglich ist, eine Route zu finden, die genau einmal über jede Brücke führt. Das heißt, bei unserem Spaziergang durch die Stadt wollen wir, dass unsere Route über jede Brücke führt, aber sie kann nicht zweimal oder dreimal darüber führen… Im Grunde genommen ist der Weg ungültig, wenn man sich auf derselben Brücke wiederfindet, auf der man vorher war. Wenn du deine Wanderung beendest und es gibt eine Brücke, die du nicht überquert hast, dann war deine Route ungültig.
Die Lösung
Betrachte jeden Landfleck. Jede Brücke ist mit zwei Klecksen Land verbunden (so funktionieren Brücken). Jeder Landfleck hat zufällig eine ungerade Anzahl von Brücken.
Betrachten wir nun, wie ein gültiger Spaziergang aussehen würde.
Während du deinen Spaziergang machst, notierst du jedes Mal, wenn du dich in einem bestimmten Landfleck befindest, in einem Notizblock. Wenn du zum Beispiel am südlichsten Ende der Stadt beginnst, notierst du das (mach ein Foto, kauf ein Souvenir…) und wenn du dich dort wiederfindest, erhöhst du die Zahl für den südlichen Sektor auf zwei.
Für jeden Fleck Land gibt es zwei Fälle
(1) dies ist ein Abschnitt der Stadt, in dem wir unseren Spaziergang weder beginnen noch beenden
(2) dies ist ein Abschnitt der Stadt, in dem wir unseren Spaziergang entweder beginnen oder beenden oder beides.
Klarerweise gibt es höchstens 2 Abschnitte der Stadt vom zweiten Typ. Wir können weder an zwei Orten gleichzeitig beginnen, noch können wir an zwei Orten gleichzeitig enden.
Da es vier Stadtteile gibt, bedeutet das, dass es mindestens zwei Stadtteile gibt, in denen wir unseren Spaziergang weder beginnen noch beenden. Wählen wir einen davon aus.
Wenn wir in diesen Sektor gehen, benutzen wir eine Brücke, und wenn wir ihn verlassen, benutzen wir eine andere. Aber jeder Sektor hat eine ungerade Anzahl von Brücken, die mit ihm verbunden sind! Das ist ein Widerspruch. Um zu sehen, warum das so ist, erinnere dich daran, dass jeder Sektor entweder 3 Brücken oder 5 Brücken hat.
Wenn wir einmal in einem Sektor sind, können wir nur zwei seiner Brücken benutzen. Wenn wir zweimal in diesem Sektor sind, können wir vier seiner Brücken nutzen (oder uns gehen die Brücken aus, wenn er nur drei Brücken hat). Bei dreimaligem Betreten würden wir 6 Brücken benötigen, die wir nicht haben können. Die Bedingung, dass wir einen Sektor der Stadt, der weder unser Start- noch unser Endpunkt ist, sowohl betreten als auch verlassen müssen, widerspricht also der Tatsache, dass die Anzahl der Verbindungsbrücken für jeden Sektor ungerade ist.