Was ist der Kernel-Trick? Warum ist er wichtig?
Wenn man über Kernel im maschinellen Lernen spricht, kommt einem wahrscheinlich als erstes das Modell der Support-Vektor-Maschinen (SVM) in den Sinn, denn der Kernel-Trick wird im SVM-Modell häufig verwendet, um Linearität und Nichtlinearität zu überbrücken.
Damit Sie verstehen, was ein Kernel ist und warum er wichtig ist, werde ich Ihnen zunächst die Grundlagen des SVM-Modells erläutern.
Das SVM-Modell ist ein überwachtes maschinelles Lernmodell, das hauptsächlich für Klassifizierungen verwendet wird (es kann aber auch für Regressionen eingesetzt werden!). Es lernt, wie man verschiedene Gruppen trennt, indem es Entscheidungsgrenzen bildet.

In der obigen Grafik sehen wir, dass es zwei Klassen von Beobachtungen gibt: die blauen Punkte und die violetten Punkte. Es gibt viele Möglichkeiten, diese beiden Klassen zu trennen, wie das Diagramm links zeigt. Wir wollen jedoch die „beste“ Hyperebene finden, die den Abstand zwischen diesen beiden Klassen maximiert, d. h. der Abstand zwischen der Hyperebene und den nächstgelegenen Datenpunkten auf jeder Seite ist am größten. Je nachdem, auf welcher Seite der Hyperebene sich ein neuer Datenpunkt befindet, können wir der neuen Beobachtung eine Klasse zuordnen.
Im obigen Beispiel klingt das einfach. Doch nicht alle Daten sind linear trennbar. Tatsächlich sind in der realen Welt fast alle Daten zufällig verteilt, was es schwierig macht, verschiedene Klassen linear zu trennen.

Warum ist es wichtig, den Kernel-Trick anzuwenden?
Wie Sie in der obigen Abbildung sehen können, können wir, wenn wir einen Weg finden, die Daten vom zweidimensionalen in den dreidimensionalen Raum umzuwandeln, eine Entscheidungsfläche finden, die klar zwischen verschiedenen Klassen trennt. Mein erster Gedanke bei diesem Datentransformationsprozess ist, alle Datenpunkte auf eine höhere Dimension (in diesem Fall 3 Dimension) abzubilden, die Grenze zu finden und die Klassifizierung vorzunehmen.
Das klingt gut. Wenn es jedoch immer mehr Dimensionen gibt, werden die Berechnungen innerhalb dieses Raums immer teurer. An dieser Stelle kommt der Kernel-Trick ins Spiel. Er ermöglicht es uns, im ursprünglichen Merkmalsraum zu operieren, ohne die Koordinaten der Daten in einem höherdimensionalen Raum zu berechnen.
Lassen Sie uns ein Beispiel betrachten:
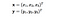
Hier sind x und y zwei Datenpunkte in 3 Dimensionen. Nehmen wir an, dass wir x und y auf den 9-dimensionalen Raum abbilden müssen. Wir müssen die folgenden Berechnungen durchführen, um das Endergebnis zu erhalten, das nur ein Skalar ist. Die Rechenkomplexität ist in diesem Fall O(n²).

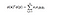
However, if we use the kernel function, which is denoted as k(x, y), instead of doing the complicated computations in the 9-dimensional space, we reach the same result within the 3-dimensional space by calculating the dot product of x -transpose and y. The computational complexity, in this case, is O(n).
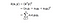
In essence, what the kernel trick does for us is to offer a more efficient and less expensive way to transform data into higher dimensions. With that saying, the application of the kernel trick is not limited to the SVM algorithm. Alle Berechnungen, die Punktprodukte (x, y) beinhalten, können den Kernel-Trick nutzen.
Unterschiedliche Kernel-Funktionen
Es gibt verschiedene Kernel. Die bekanntesten sind der Polynom-Kernel und der Radial Basis Function (RBF)-Kernel.
„Intuitiv betrachtet der Polynom-Kernel nicht nur die gegebenen Merkmale der Eingabemuster, um ihre Ähnlichkeit zu bestimmen, sondern auch Kombinationen davon“ (Wikipedia), wie im obigen Beispiel. Bei n ursprünglichen Merkmalen und d Polynomgraden ergibt der Polynomkern n^d erweiterte Merkmale.
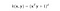
Der RBF-Kernel wird auch Gauß-Kernel genannt. Es gibt eine unendliche Anzahl von Dimensionen im Merkmalsraum, da er durch die Taylorreihe erweitert werden kann. Im folgenden Format gibt der Parameter γ an, wie groß der Einfluss eines einzelnen Trainingsbeispiels ist. Je größer er ist, desto näher müssen andere Beispiele sein, um beeinflusst zu werden (sklearn-Dokumentation).
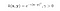
Es gibt verschiedene Optionen für die Kernel-Funktionen in der sklearn-Bibliothek in Python. Bei Bedarf können Sie sogar einen eigenen Kernel erstellen.
Das Ende
Der Kernel-Trick klingt nach einem „perfekten“ Plan. Allerdings muss man bedenken, dass bei der Abbildung von Daten auf eine höhere Dimension die Gefahr besteht, dass das Modell übermäßig angepasst wird. Daher sind die Wahl der richtigen Kernel-Funktion (einschließlich der richtigen Parameter) und die Regularisierung von großer Bedeutung.
Wenn Sie wissen möchten, was Regularisierung ist, habe ich einen Artikel über mein Verständnis davon geschrieben, den Sie hier finden können.
Ich hoffe, dieser Artikel gefällt Ihnen. Bitte lassen Sie mich wie immer wissen, wenn Sie Fragen, Kommentare, Vorschläge usw. haben. Danke fürs Lesen 🙂