Was ist ein Tiefpassfilter? Ein Tutorial über die Grundlagen von passiven RC-Filtern

Dezember 5, 2021admin

Was ist ein Filter? Erfahren Sie, was Widerstandskondensator-Tiefpassfilter (RC-Filter) sind und wo Sie sie einsetzen können.

Dieser Artikel führt in das Konzept der Filterung ein und erklärt ausführlich den Zweck und die Eigenschaften von Widerstandskondensator-Tiefpassfiltern (RC-Filtern).

Zeitbereich und Frequenzbereich

Wenn Sie ein elektrisches Signal auf einem Oszilloskop betrachten, sehen Sie eine Linie, die Spannungsänderungen im Verhältnis zur Zeit darstellt. Zu jedem bestimmten Zeitpunkt hat das Signal nur einen einzigen Spannungswert. Was Sie auf dem Oszilloskop sehen, ist die Darstellung des Signals im Zeitbereich.

Eine typische Oszilloskopkurve ist einfach und intuitiv, aber auch etwas einschränkend, da sie den Frequenzgehalt eines Signals nicht direkt erkennen lässt. Im Gegensatz zur Darstellung im Zeitbereich, bei der ein Moment in der Zeit nur einem Spannungswert entspricht, vermittelt eine Darstellung im Frequenzbereich (auch Spektrum genannt) Informationen über ein Signal, indem sie die verschiedenen Frequenzkomponenten identifiziert, die gleichzeitig vorhanden sind.

Darstellungen im Zeitbereich einer Sinuskurve (oben) und einer Rechteckwelle (unten).

Darstellungen einer Sinuswelle (oben) und einer Rechteckwelle (unten) im Frequenzbereich.

Was ist ein Filter?

Ein Filter ist eine Schaltung, die einen bestimmten Bereich von Frequenzkomponenten entfernt oder „herausfiltert“. Mit anderen Worten, er trennt das Spektrum des Signals in Frequenzkomponenten, die durchgelassen werden, und in Frequenzkomponenten, die blockiert werden.

Wenn Sie noch nicht viel Erfahrung mit der Analyse im Frequenzbereich haben, sind Sie vielleicht noch unsicher, was diese Frequenzkomponenten sind und wie sie in einem Signal koexistieren, das nicht mehrere Spannungswerte gleichzeitig haben kann. Schauen wir uns ein kurzes Beispiel an, um dieses Konzept zu verdeutlichen.

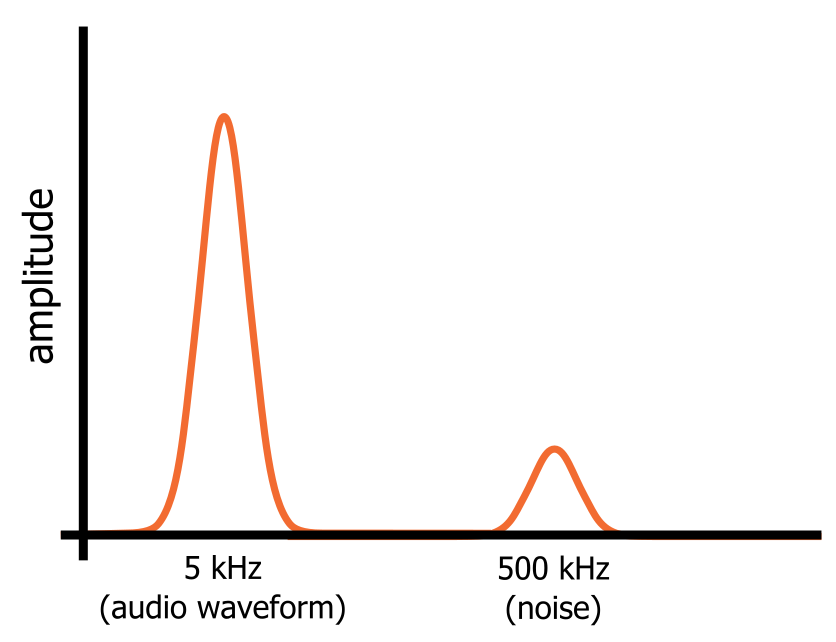
Stellen wir uns vor, wir haben ein Audiosignal, das aus einer perfekten 5-kHz-Sinuswelle besteht. Wir wissen, wie eine Sinuswelle im Zeitbereich aussieht, und im Frequenzbereich sehen wir nichts anderes als eine „Frequenzspitze“ bei 5 kHz. Nehmen wir nun an, dass wir einen 500-kHz-Oszillator aktivieren, der hochfrequentes Rauschen in das Audiosignal einbringt.

Das Signal, das wir auf einem Oszilloskop sehen, ist immer noch eine einzige Spannungssequenz mit einem Wert pro Zeit, aber das Signal sieht anders aus, weil seine Variationen im Zeitbereich nun sowohl die 5-kHz-Sinuswelle als auch die hochfrequenten Rauschschwankungen widerspiegeln müssen.

Im Frequenzbereich sind die Sinuswelle und das Rauschen jedoch separate Frequenzkomponenten, die gleichzeitig in diesem einen Signal vorhanden sind. Das bedeutet, dass wir das Rauschen herausfiltern können, indem wir das Signal durch eine Schaltung leiten, die niedrige Frequenzen durchlässt und hohe Frequenzen blockiert.

Typen von Filtern

Filter können in grobe Kategorien eingeteilt werden, die den allgemeinen Eigenschaften des Frequenzgangs des Filters entsprechen. Wenn ein Filter tiefe Frequenzen durchlässt und hohe Frequenzen blockiert, nennt man es einen Tiefpassfilter. Wenn er tiefe Frequenzen sperrt und hohe Frequenzen durchlässt, ist er ein Hochpassfilter. Es gibt auch Bandpassfilter, die nur einen relativ schmalen Frequenzbereich durchlassen, und Bandsperrfilter, die nur einen relativ schmalen Frequenzbereich sperren.

Filter können auch nach der Art der Komponenten klassifiziert werden, die zur Implementierung der Schaltung verwendet werden. Bei passiven Filtern werden Widerstände, Kondensatoren und Induktivitäten verwendet; diese Bauteile können keine Verstärkung bewirken, so dass ein passiver Filter die Amplitude eines Eingangssignals nur aufrechterhalten oder verringern kann. Ein aktiver Filter hingegen kann ein Signal sowohl filtern als auch verstärken, da er ein aktives Bauelement wie einen Transistor oder einen Operationsverstärker enthält.

Dieser aktive Tiefpassfilter basiert auf der beliebten Sallen-Key-Topologie.

Dieser Artikel befasst sich mit der Analyse und dem Entwurf von passiven Tiefpassfiltern. Diese Schaltungen spielen eine wichtige Rolle in einer Vielzahl von Systemen und Anwendungen.

Der RC-Tiefpassfilter

Um einen passiven Tiefpassfilter zu erstellen, müssen wir ein Widerstandselement mit einem reaktiven Element kombinieren. Mit anderen Worten, wir brauchen eine Schaltung, die aus einem Widerstand und entweder einem Kondensator oder einer Spule besteht. Theoretisch ist die Widerstand-Induktor (RL)-Tiefpass-Topologie in Bezug auf die Filterleistung gleichwertig mit der Widerstand-Kondensator (RC)-Tiefpass-Topologie. In der Praxis ist jedoch die Widerstand-Kondensator-Variante weitaus häufiger anzutreffen, weshalb sich der Rest dieses Artikels auf den RC-Tiefpassfilter konzentriert.

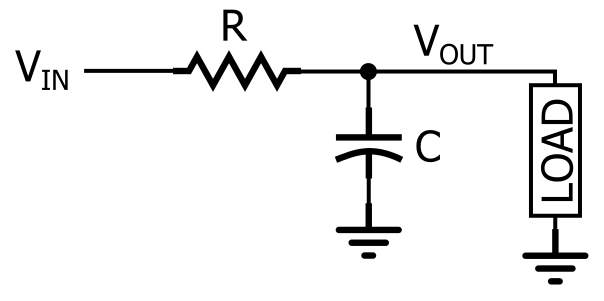
Der RC-Tiefpassfilter.

Wie im Diagramm zu sehen ist, wird ein RC-Tiefpass erzeugt, indem ein Widerstand in Reihe mit dem Signalweg und ein Kondensator parallel zur Last geschaltet wird. Im Diagramm ist die Last ein einzelnes Bauteil, aber in einer realen Schaltung kann es sich um etwas viel Komplizierteres handeln, z. B. einen Analog-Digital-Wandler, einen Verstärker oder die Eingangsstufe des Oszilloskops, das Sie zur Messung der Filterantwort verwenden.

Wir können die Filterwirkung der RC-Tiefpass-Topologie intuitiv analysieren, wenn wir erkennen, dass der Widerstand und der Kondensator einen frequenzabhängigen Spannungsteiler bilden.

Der RC-Tiefpassfilter so gezeichnet, dass er wie ein Spannungsteiler aussieht.

Wenn die Frequenz des Eingangssignals niedrig ist, ist die Impedanz des Kondensators im Verhältnis zur Impedanz des Widerstands hoch; daher fällt der größte Teil der Eingangsspannung über den Kondensator ab (und über die Last, die parallel zum Kondensator liegt). Wenn die Eingangsfrequenz hoch ist, ist die Impedanz des Kondensators im Verhältnis zur Impedanz des Widerstands niedrig, was bedeutet, dass mehr Spannung über den Widerstand abfällt und weniger an die Last übertragen wird. So werden niedrige Frequenzen durchgelassen und hohe Frequenzen blockiert.

Diese qualitative Erklärung der RC-Tiefpass-Funktionalität ist ein wichtiger erster Schritt, aber sie ist nicht sehr hilfreich, wenn es darum geht, eine Schaltung zu entwerfen, denn die Begriffe „hohe Frequenz“ und „niedrige Frequenz“ sind äußerst vage. Ingenieure müssen Schaltungen entwerfen, die bestimmte Frequenzen durchlassen oder blockieren. In dem oben beschriebenen Audiosystem wollen wir zum Beispiel ein 5-kHz-Signal erhalten und ein 500-kHz-Signal unterdrücken. Das bedeutet, dass wir einen Filter brauchen, der irgendwo zwischen 5 kHz und 500 kHz vom Durchlass zum Sperren übergeht.

Die Grenzfrequenz

Der Bereich der Frequenzen, für die ein Filter keine signifikante Dämpfung verursacht, wird als Durchlassbereich bezeichnet, und der Bereich der Frequenzen, für die der Filter eine signifikante Dämpfung verursacht, als Sperrbereich. Analoge Filter, wie z. B. RC-Tiefpassfilter, gehen immer allmählich vom Durchlassbereich zum Sperrbereich über. Das bedeutet, dass es unmöglich ist, eine bestimmte Frequenz zu bestimmen, bei der der Filter keine Signale mehr durchlässt und Signale blockiert. Ingenieure benötigen jedoch eine Möglichkeit, den Frequenzgang eines Filters bequem und prägnant zusammenzufassen, und hier kommt das Konzept der Grenzfrequenz ins Spiel.

Wenn Sie sich eine Darstellung des Frequenzgangs eines RC-Filters ansehen, werden Sie feststellen, dass der Begriff „Grenzfrequenz“ nicht sehr genau ist. Die Vorstellung, dass das Spektrum eines Signals in zwei Hälften „geschnitten“ wird, von denen eine erhalten bleibt und die andere verworfen wird, trifft nicht zu, da die Dämpfung allmählich zunimmt, wenn sich die Frequenzen von unterhalb der Grenzfrequenz nach oberhalb der Grenzfrequenz bewegen.

Die Grenzfrequenz eines RC-Tiefpassfilters ist eigentlich die Frequenz, bei der die Amplitude des Eingangssignals um 3 dB verringert wird (dieser Wert wurde gewählt, weil eine Verringerung der Amplitude um 3 dB einer Verringerung der Leistung um 50 % entspricht). Daher wird die Grenzfrequenz auch als -3-dB-Frequenz bezeichnet, und in der Tat ist diese Bezeichnung genauer und informativer. Der Begriff Bandbreite bezieht sich auf die Breite des Durchlassbereichs eines Filters, und im Falle eines Tiefpassfilters ist die Bandbreite gleich der -3-dB-Frequenz (wie im folgenden Diagramm dargestellt).

Dieses Diagramm zeigt die allgemeinen Merkmale des Frequenzgangs eines RC-Tiefpassfilters. Die Bandbreite entspricht der -3 dB-Frequenz.

Wie oben erläutert, wird das Tiefpassverhalten eines RC-Filters durch die Wechselwirkung zwischen der frequenzunabhängigen Impedanz des Widerstands und der frequenzabhängigen Impedanz des Kondensators verursacht. Um die Details des Frequenzgangs eines Filters zu bestimmen, müssen wir die Beziehung zwischen Widerstand (R) und Kapazität (C) mathematisch analysieren und können diese Werte auch manipulieren, um einen Filter zu entwerfen, der genaue Spezifikationen erfüllt. Die Grenzfrequenz (fC) eines RC-Tiefpassfilters wird wie folgt berechnet:

Lassen Sie uns ein einfaches Designbeispiel betrachten. Kondensatorwerte sind restriktiver als Widerstandswerte, also beginnen wir mit einem üblichen Kapazitätswert (z. B. 10 nF) und verwenden dann die Gleichung, um den erforderlichen Widerstandswert zu bestimmen. Ziel ist es, einen Filter zu entwickeln, der eine 5-kHz-Audiowellenform beibehält und eine 500-kHz-Rauschwellenform unterdrückt. Wir versuchen es mit einer Grenzfrequenz von 100 kHz und werden im weiteren Verlauf des Artikels die Auswirkungen dieses Filters auf die beiden Frequenzkomponenten genauer analysieren.

Mit einem 160 Ω-Widerstand und einem 10 nF-Kondensator erhalten wir also ein Filter, das dem gewünschten Frequenzgang sehr nahe kommt.

Berechnung des Filterverhaltens

Wir können das theoretische Verhalten eines Tiefpassfilters berechnen, indem wir eine frequenzabhängige Version einer typischen Spannungsteilerberechnung verwenden. Der Ausgang eines ohmschen Spannungsteilers wird wie folgt ausgedrückt:

Der RC-Filter verwendet eine äquivalente Struktur, aber anstelle von R2 haben wir einen Kondensator. Zunächst ersetzen wir R2 (im Zähler) durch den Blindwiderstand des Kondensators (XC). Als Nächstes müssen wir den Betrag der Gesamtimpedanz berechnen und diesen in den Nenner setzen. Daraus ergibt sich

Der Blindwiderstand eines Kondensators gibt an, wie groß der Widerstand gegen den Stromfluss ist, aber im Gegensatz zum Widerstand hängt der Betrag des Widerstands von der Frequenz des Signals ab, das durch den Kondensator fließt. Daher müssen wir den Blindwiderstand bei einer bestimmten Frequenz berechnen, und die Gleichung, die wir dafür verwenden, lautet wie folgt:

Im obigen Konstruktionsbeispiel ist R ≈ 160 Ω und C = 10 nF. Wir nehmen an, dass die Amplitude von VIN 1 V beträgt, so dass wir VIN einfach aus der Berechnung entfernen können. Berechnen wir zunächst die Amplitude von VOUT bei der Sinusfrequenz:

Die Amplitude der Sinuswelle ist im Wesentlichen unverändert. Das ist gut, denn unser Ziel war es, die Sinuswelle zu erhalten und das Rauschen zu unterdrücken. Dieses Ergebnis ist nicht überraschend, da wir eine Grenzfrequenz (100 kHz) gewählt haben, die viel höher ist als die Sinuswellenfrequenz (5 kHz).

Nun wollen wir sehen, wie erfolgreich das Filter die Rauschkomponente dämpft.

Die Amplitude des Rauschens beträgt nur noch etwa 20 % des ursprünglichen Wertes.

Visualisierung der Filterantwort

Die bequemste Methode, die Wirkung eines Filters auf ein Signal zu beurteilen, ist die Betrachtung des Frequenzgangs des Filters. Diese Diagramme, die oft als Bode-Diagramme bezeichnet werden, haben den Betrag (in Dezibel) auf der vertikalen Achse und die Frequenz auf der horizontalen Achse; die horizontale Achse hat in der Regel eine logarithmische Skala, so dass der physikalische Abstand zwischen 1 Hz und 10 Hz der gleiche ist wie der physikalische Abstand zwischen 10 Hz und 100 Hz, zwischen 100 Hz und 1 kHz und so weiter. Auf diese Weise lässt sich das Verhalten eines Filters über einen sehr großen Frequenzbereich schnell und genau beurteilen.

Beispiel für eine Frequenzgangkurve.

Jeder Punkt auf der Kurve gibt den Wert an, den das Ausgangssignal hat, wenn das Eingangssignal einen Wert von 1 V und eine Frequenz hat, die dem entsprechenden Wert auf der horizontalen Achse entspricht. Beträgt die Eingangsfrequenz beispielsweise 1 MHz, so beträgt die Ausgangsamplitude (bei einer Eingangsamplitude von 1 V) 0,1 V (da -20 dB einer Verringerung um den Faktor 10 entspricht).

Die allgemeine Form dieser Frequenzgangkurve wird Ihnen sehr vertraut sein, wenn Sie mehr Zeit mit Filterschaltungen verbringen. Die Kurve ist im Durchlassbereich fast vollkommen flach und beginnt dann schneller abzufallen, wenn sich die Eingangsfrequenz der Grenzfrequenz nähert. Schließlich stabilisiert sich die Änderungsrate der Dämpfung, der so genannte Roll-Off, bei 20 dB/Dekade, d. h. der Betrag des Ausgangssignals wird bei jeder Erhöhung der Eingangsfrequenz um einen Zehnerfaktor um 20 dB verringert.

Bewertung der Leistung von Tiefpassfiltern

Wenn wir den Frequenzgang des Filters, den wir in diesem Artikel entworfen haben, sorgfältig aufzeichnen, sehen wir, dass der Betragsgang bei 5 kHz im Wesentlichen 0 dB beträgt (d. h., (d. h. fast keine Dämpfung) und der Amplitudengang bei 500 kHz etwa -14 dB beträgt (was einer Verstärkung von 0,2 entspricht). Diese Werte stimmen mit den Ergebnissen der Berechnungen überein, die wir im vorigen Abschnitt durchgeführt haben.

Da RC-Filter immer einen allmählichen Übergang vom Durchlassbereich zum Sperrbereich haben und die Dämpfung nie unendlich ist, können wir kein „perfektes“ Filter entwerfen, d. h. ein Filter, das keine Auswirkungen auf die Sinuswelle hat und das Rauschen vollständig eliminiert. Stattdessen müssen wir immer einen Kompromiss eingehen. Wenn wir die Cutoff-Frequenz näher an 5 kHz heranbringen, wird das Rauschen stärker gedämpft, aber auch die Sinuswelle, die wir an einen Lautsprecher senden wollen, wird stärker gedämpft. Wenn wir die Grenzfrequenz näher an 500 kHz heranbringen, haben wir eine geringere Dämpfung der Sinuswellenfrequenz, aber auch eine geringere Dämpfung der Rauschfrequenz.

Tiefpassfilter-Phasenverschiebung

Bislang haben wir erörtert, wie ein Filter die Amplitude der verschiedenen Frequenzkomponenten in einem Signal verändert. Reaktive Schaltungselemente bewirken jedoch zusätzlich zu den Amplitudeneffekten immer auch eine Phasenverschiebung.

Der Begriff der Phase bezieht sich auf den Wert eines periodischen Signals zu einem bestimmten Zeitpunkt innerhalb eines Zyklus. Wenn wir also sagen, dass eine Schaltung eine Phasenverschiebung verursacht, meinen wir damit, dass sie eine Verschiebung zwischen dem Eingangssignal und dem Ausgangssignal bewirkt: Die Eingangs- und Ausgangssignale beginnen und enden ihre Zyklen nicht mehr zum gleichen Zeitpunkt. Der Wert der Phasenverschiebung, z. B. 45° oder 90°, gibt an, wie stark die Phasenverschiebung ist.

Jedes reaktive Element in einer Schaltung verursacht eine Phasenverschiebung von 90°, aber diese Phasenverschiebung geschieht nicht auf einmal. Die Phase des Ausgangssignals ändert sich, genau wie der Betrag des Ausgangssignals, allmählich, wenn die Eingangsfrequenz steigt. In einem RC-Tiefpassfilter gibt es nur ein reaktives Element (den Kondensator), so dass die Schaltung schließlich eine Phasenverschiebung von 90° bewirkt.

Wie der Betragsverlauf lässt sich auch der Phasenverlauf am einfachsten anhand eines Diagramms beurteilen, bei dem die horizontale Achse die logarithmische Frequenz angibt. Die nachstehende Beschreibung vermittelt das allgemeine Muster, und Sie können dann die Einzelheiten durch Untersuchung der Darstellung vervollständigen.

Die Phasenverschiebung beträgt anfangs 0°.
Sie nimmt allmählich zu, bis sie bei der Grenzfrequenz 45° erreicht; während dieses Teils der Reaktion nimmt die Änderungsrate zu.
Nach der Grenzfrequenz nimmt die Phasenverschiebung weiter zu, aber die Änderungsrate nimmt ab.
Die Änderungsrate wird sehr klein, wenn sich die Phasenverschiebung asymptotisch 90° nähert.

Die durchgezogene Linie ist der Betragsverlauf und die gepunktete Linie ist der Phasenverlauf. Die Grenzfrequenz beträgt 100 kHz. Beachten Sie, dass die Phasenverschiebung bei der Grenzfrequenz 45° beträgt.

Tiefpassfilter zweiter Ordnung

Bislang haben wir angenommen, dass ein RC-Tiefpassfilter aus einem Widerstand und einem Kondensator besteht. Diese Konfiguration ist ein Filter erster Ordnung.

Die „Ordnung“ eines passiven Filters wird durch die Anzahl der reaktiven Elemente – d.h. Kondensatoren oder Induktoren – bestimmt, die in der Schaltung vorhanden sind. Ein Filter höherer Ordnung hat mehr reaktive Elemente, was zu einer größeren Phasenverschiebung und einem steileren Abfall führt. Diese zweite Eigenschaft ist die Hauptmotivation für die Erhöhung der Ordnung eines Filters.

Wenn man ein reaktives Element zu einem Filter hinzufügt – z. B. indem man von erster Ordnung zu zweiter Ordnung oder von zweiter zu dritter Ordnung übergeht -, erhöht sich der maximale Roll-off um 20 dB/Dekade. Ein steilerer Roll-Off bedeutet einen schnelleren Übergang von einer niedrigen Dämpfung zu einer hohen Dämpfung, was zu einer verbesserten Leistung führen kann, wenn das Signal kein breites Frequenzband aufweist, das die gewünschten Frequenzkomponenten von den Rauschkomponenten trennt.

Filter zweiter Ordnung sind in der Regel um einen Schwingkreis herum aufgebaut, der aus einer Spule und einem Kondensator besteht (diese Topologie wird als „RLC“ für Resistor-Induktor-Capacitor bezeichnet). Es ist jedoch auch möglich, RC-Filter zweiter Ordnung zu erstellen. Wie im folgenden Diagramm dargestellt, müssen lediglich zwei RC-Filter erster Ordnung kaskadiert werden.

Obwohl diese Topologie einen Frequenzgang zweiter Ordnung erzeugt, wird sie nicht häufig verwendet – wie wir im nächsten Abschnitt sehen werden, ist der Frequenzgang oft schlechter als der eines aktiven Filters zweiter Ordnung oder eines RLC-Filters zweiter Ordnung.

Frequenzgang des RC-Filters zweiter Ordnung

Wir können versuchen, ein RC-Tiefpassfilter zweiter Ordnung zu erstellen, indem wir ein Filter erster Ordnung entsprechend der gewünschten Grenzfrequenz entwerfen und dann zwei dieser Stufen erster Ordnung in Reihe schalten. Das Ergebnis ist ein Filter mit einem ähnlichen Gesamtfrequenzgang und einem maximalen Abfall von 40 dB/Dekade statt 20 dB/Dekade.

Bei genauerer Betrachtung des Frequenzgangs ist jedoch festzustellen, dass die -3 dB-Frequenz gesunken ist. Der RC-Filter zweiter Ordnung verhält sich nicht wie erwartet, weil die beiden Stufen nicht unabhängig sind – wir können diese beiden Stufen nicht einfach miteinander verbinden und die Schaltung als Tiefpassfilter erster Ordnung analysieren, gefolgt von einem identischen Tiefpassfilter erster Ordnung.

Auch wenn wir einen Puffer zwischen die beiden Stufen einfügen, so dass die erste RC-Stufe und die zweite RC-Stufe als unabhängige Filter funktionieren können, beträgt die Dämpfung bei der ursprünglichen Grenzfrequenz 6 dB statt 3 dB. Dies geschieht genau deshalb, weil die beiden Stufen unabhängig voneinander arbeiten – der erste Filter hat eine Dämpfung von 3 dB bei der Grenzfrequenz, und der zweite Filter fügt eine weitere Dämpfung von 3 dB hinzu.

Die grundsätzliche Einschränkung des RC-Tiefpassfilters zweiter Ordnung besteht darin, dass der Designer den Übergang vom Durchlassbereich zum Sperrbereich nicht fein abstimmen kann, indem er den Q-Faktor des Filters anpasst; dieser Parameter gibt an, wie gedämpft der Frequenzgang ist. Wenn Sie zwei identische RC-Tiefpassfilter kaskadieren, entspricht die Gesamtübertragungsfunktion einer Antwort zweiter Ordnung, aber der Q-Faktor ist immer 0,5. Wenn Q = 0,5 ist, befindet sich das Filter an der Grenze zur Überdämpfung, und dies führt zu einem Frequenzgang, der im Übergangsbereich „durchhängt“. Bei aktiven Filtern zweiter Ordnung und resonanzbasierten Filtern zweiter Ordnung gibt es diese Einschränkung nicht; der Konstrukteur kann den Q-Faktor steuern und so den Frequenzgang im Übergangsbereich fein abstimmen.

Zusammenfassung

Alle elektrischen Signale enthalten eine Mischung aus erwünschten Frequenzkomponenten und unerwünschten Frequenzkomponenten. Die unerwünschten Frequenzanteile werden in der Regel durch Rauschen und Störungen verursacht und beeinträchtigen in manchen Situationen die Leistung des Systems.
Ein Filter ist eine Schaltung, die auf unterschiedliche Weise auf verschiedene Teile des Spektrums eines Signals reagiert. Ein Tiefpassfilter ist so konzipiert, dass er niederfrequente Komponenten durchlässt und hochfrequente Komponenten blockiert.
Die Grenzfrequenz eines Tiefpassfilters gibt den Frequenzbereich an, in dem der Filter von einer geringen Dämpfung zu einer erheblichen Dämpfung übergeht.
Die Ausgangsspannung eines RC-Tiefpassfilters kann berechnet werden, indem man die Schaltung als einen Spannungsteiler behandelt, der aus einem (frequenzunabhängigen) Widerstand und einer (frequenzabhängigen) Reaktanz besteht.
Eine Darstellung des Betrags (in dB, auf der vertikalen Achse) gegen die logarithmische Frequenz (in Hertz, auf der horizontalen Achse) ist eine bequeme und effektive Methode, um das theoretische Verhalten eines Filters zu untersuchen. Sie können auch ein Diagramm der Phase gegen die logarithmische Frequenz verwenden, um den Betrag der Phasenverschiebung zu bestimmen, der auf ein Eingangssignal angewendet wird.
Ein Filter zweiter Ordnung bietet einen steileren Abfall; diese Reaktion zweiter Ordnung ist hilfreich, wenn ein Signal kein breites Band der Trennung zwischen gewünschten Frequenzkomponenten und unerwünschten Frequenzkomponenten bietet.
Sie können ein RC-Tiefpassfilter zweiter Ordnung erstellen, indem Sie zwei identische RC-Tiefpassfilter erster Ordnung bauen und dann den Ausgang des einen mit dem Eingang des anderen verbinden. Die Gesamt-3-dB-Frequenz wird niedriger sein als erwartet.