2.3D: Teoría de la separación

Teoría general

La cromatografía de capa fina (TLC) es una excelente herramienta analítica para separar mezclas en una muestra. En esta sección se discuten los detalles de la separación, y se amplía la discusión general de la Sección 2.1.B.

En todas las formas de cromatografía, las muestras se equilibran entre las fases estacionaria y móvil. En casi todas las aplicaciones de la TLC, la fase estacionaria es un adsorbente de sílice o alúmina y la fase móvil es un disolvente orgánico o una mezcla de disolventes (el «eluyente») que asciende por la placa (ecuación 3).

El gel de sílice (mostrado en la figura 2.16) está compuesto por una red de enlaces silicio-oxígeno, con enlaces \(\ce{O-H}\ en su superficie, así como una capa de moléculas de agua. El gel de sílice (izquierda) es utilizado en esta discusión, pero es estructuralmente análogo a la alúmina (izquierda). Esta fase estacionaria muy polar se combina con una fase móvil relativamente no polar (un disolvente o solución orgánica), en lo que se denomina TLC de «fase normal». Aunque ésta es la forma más común de TLC (y en la que nos centraremos en esta sección), a veces se utiliza la TLC de «fase inversa» (con una fase estacionaria no polar y una fase móvil polar).

La figura 2.16 muestra cómo la acetofenona se aferraría a la superficie del gel de sílice a través de las fuerzas intermoleculares (FMI). En este caso, la acetofenona puede formar un enlace de hidrógeno (la FMI indicada en la figura 2.16a) con la superficie de sílice a través de su átomo de oxígeno. A medida que el eluyente fluye sobre la muestra (Figura 2.16b), se establece un equilibrio entre la muestra adsorbida en la fase estacionaria y la disuelta en la fase móvil. Cuando se encuentra en la fase móvil, el compuesto se desplaza hacia arriba en la placa con el flujo de líquido (Figura 2.16c) para posteriormente readsorberse en la fase estacionaria más arriba en la placa. El \ (R_f\) resultante del compuesto depende de la cantidad de tiempo que pasa en las fases estacionaria y móvil.

La distribución de equilibrio entre las dos fases depende de varios factores:

1. Depende de la fuerza de las fuerzas intermoleculares entre la muestra y la fase estacionaria.
   Un compuesto que forma fuertes FMI con la sílice o la alúmina a menudo favorecerá la fase estacionaria, y pasará gran parte del tiempo de elución adherido a la placa. Esto significa que pasará menos tiempo en la fase móvil (que es el único medio para que suba por la placa), lo que hace que termine en la parte baja de la placa de TLC y tenga un \ (R_f\) bajo.
   Los compuestos que tienen átomos de oxígeno o nitrógeno deberían ser capaces de establecer enlaces de hidrógeno con la fase estacionaria (tienen fuertes FMI con la fase estacionaria) y, por lo tanto, tendrán valores de \ (R_f\) más bajos que los compuestos de tamaño similar que sólo pueden interactuar a través de las fuerzas de dispersión de London (LDF).
2. Depende de la fuerza de interacción entre la muestra y la fase móvil.
   Como la fase móvil es siempre menos polar que la fase estacionaria en la TLC de fase normal, los compuestos polares tenderán a tener una menor afinidad por la fase móvil que los compuestos no polares (basándose en el principio de «lo similar se disuelve de forma similar»). Por lo tanto, los compuestos polares tienden a pasar menos del tiempo de elución móvil que un compuesto no polar, por lo que viajarán «más lentamente» hacia arriba en la placa, y tendrán una baja \ (R_f\).

El grado de atracción de un compuesto hacia la fase estacionaria y la fase móvil lleva a la misma conclusión:

• Cuanto más fuerte sea el FMI con la fase estacionaria (a menudo cuanto más grupos funcionales polares tenga un compuesto), más tiempo estará el compuesto en la fase estacionaria \(R_f\) más bajo.
• Cuantos más grupos funcionales polares haya en un compuesto, menos tiende a ser atraído por el eluyente menos polar, y menos tiempo será móvil el compuesto \(\rightarrow\) menor \(R_f\).

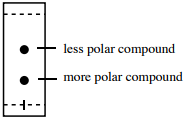
Así, un compuesto con un \(R_f\) menor tiende a tener más grupos funcionales polares que un compuesto con un \(R_f\) mayor (resumido en la Figura 2.17).