dB: ¿Qué es un decibelio?

Presión sonora, nivel sonoro y dB. El sonido se suele medir con micrófonos y éstos responden proporcionalmente a la presión sonora, p. Ahora bien, la potencia en una onda sonora, en igualdad de condiciones, va como el cuadrado de la presión. (Del mismo modo, la potencia eléctrica en una resistencia va como el cuadrado de la tensión). El logaritmo de x2 es simplemente 2 log x, así que esto introduce un factor de 2 cuando convertimos las relaciones de presión en decibelios. Por tanto, la diferencia de nivel de presión sonora entre dos sonidos con p1 y p2 es:

20 log (p2/p1) dB = 10 log (p22/p12) dB = 10 log (P2/P1) dB (en todo, el logaritmo está en base 10).

¿Qué ocurre cuando se reduce la potencia sonora a la mitad? El logaritmo de 2 es 0,3010, por lo que el logaritmo de 1/2 es -0,3, con una buena aproximación. Por tanto, si reduces la potencia a la mitad, reduces la potencia y el nivel sonoro en 3 dB. Si se vuelve a reducir a la mitad (hasta 1/4 de la potencia original), se reduce el nivel en otros 3 dB. Si sigues reduciendo la potencia a la mitad, tienes estas proporciones.

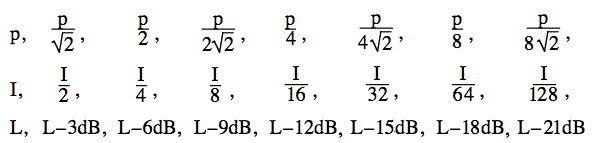
¿Qué pasa si añado dos sonidos idénticos? ¿Doblamos la intensidad (aumento de 3 dB)? O doblo la presión (aumento de 6 dB)? Esta pregunta frecuente es un poco sutil, por lo que se discute aquí en nuestro FAQ.

Archivos de sonido para mostrar el tamaño de un decibelio

Hemos visto más arriba que al reducir la potencia a la mitad se reduce la presión sonora en √2 y el nivel sonoro en 3 dB. Eso es lo que hemos hecho en el primer gráfico y en el archivo de sonido de abajo.

La primera muestra de sonido es ruido blanco (una mezcla de una amplia gama de frecuencias audibles, análoga a la luz blanca, que es una mezcla de todas las frecuencias visibles). La segunda muestra es el mismo ruido, con la tensión reducida por un factor de √2. Ahora 1/√2 es aproximadamente 0,7, por lo que -3 dB corresponde a reducir el voltaje o la presión al 70% de su valor original. La línea verde muestra la tensión en función del tiempo. La línea roja muestra un descenso exponencial continuo con el tiempo. Obsérvese que el voltaje cae un 50% por cada segundo de muestra. Nótese también que una duplicación de la potencia no supone una gran diferencia en la sonoridad. Hablaremos de esto más adelante, pero es algo útil para recordar cuando se elige un equipo de reproducción de sonido. Archivos de sonido y animación de John Tann y George Hatsidimitris.

¿Qué tamaño tiene un decibelio? En la siguiente serie, las muestras sucesivas se reducen en un solo decibelio.

Un decibelio es del mismo orden que la diferencia apenas perceptible (JND) para el nivel de sonido. Al escuchar estos archivos, te darás cuenta de que el último es más silencioso que el primero, pero es bastante menos claro para el oído que el segundo de cualquier par es más silencioso que su predecesor. 10*log10(1,26) = 1, por lo que para aumentar el nivel de sonido en 1 dB, hay que aumentar la potencia en un 26%, o la tensión en un 12%.

¿Y si la diferencia es inferior a un decibelio? Los niveles sonoros rara vez se dan con decibelios. La razón es que los niveles de sonido que difieren en menos de 1 dB son difíciles de distinguir, como muestra el siguiente ejemplo.(Esto hace que el dB sea una unidad de tamaño conveniente.)

Pasos de 0,3 dB. Puedes notar que el último es más silencioso que el primero, pero es difícil notar la diferencia entre pares sucesivos. 10*log10(1,07) = 0,3, por lo que para aumentar el nivel sonoro en 0,3 dB, hay que aumentar la potencia en un 7%, o la tensión en un 3,5%.

Niveles de referencia estándar. (nivel sonoro ‘absoluto’)

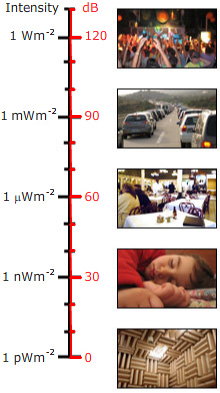Hemos dicho más arriba que el decibelio es un cociente. Por tanto, cuando se utiliza para dar el nivel sonoro de un solo sonido en lugar de una relación, hay que elegir un nivel de referencia. En el caso del nivel de presión sonora, el nivel de referencia (para el aire) suele elegirse como pref = 20 micropascales (20 μPa), es decir, 0,02 mPa. Esto es muy bajo: son 2 diezmil millonésimas partes de una atmósfera. Sin embargo, se trata del límite de sensibilidad del oído humano, en su rango sensible de frecuencia. (Por lo general, esta sensibilidad sólo se encuentra en personas más bien jóvenes o en personas que no han estado expuestas a música alta u otros ruidos fuertes. Los sistemas personales de música con altavoces en el oído son capaces de producir niveles de sonido muy altos en el oído, y algunos creen que son responsables de gran parte de la pérdida de audición en adultos jóvenes en algunos países).

Así que si lee de un nivel de presión sonora de 86 dB, significa que

20 log (p2/pref) = 86 dB

donde pref es la presión sonora del nivel de referencia, y p2 la del sonido en cuestión. Divida ambos lados por 20:

log (p2/pref) = 4,3

p2/pref = 104,3

4 es el logaritmo de 10 mil, 0,3 es el logaritmo de 2, por lo que este sonido tiene una presión sonora 20 mil veces superior a la del nivel de referencia (p2/pref = 20.000) o una intensidad 400 millones de veces superior a la de referencia. 86 dB es un sonido fuerte pero no peligroso, siempre que la exposición sea breve.

¿Qué significa 0 dB? Este nivel se produce cuando la intensidad medida es igual al nivel de referencia, es decir, es el nivel sonoro correspondiente a 0,02 mPa. En este caso tenemos

Nivel sonoro = 20 log (pmedido/pref) = 20 log 1 = 0 dB

Recuerda que los decibelios miden una relación. 0 dB se produce cuando se toma el logaritmo de un cociente de 1 (log 1 = 0). Así que 0 dB no significa que no haya sonido, sino un nivel sonoro en el que la presión sonora es igual a la del nivel de referencia. Se trata de una presión pequeña, pero no nula. También es posible tener niveles sonoros negativos: – 20 dB significaría un sonido con una presión 10 veces menor que la de referencia, es decir, 2 μPa.

No todas las presiones sonoras son igual de fuertes. Esto se debe a que el oído humano no responde igual a todas las frecuencias: somos mucho más sensibles a los sonidos en el rango de frecuencias de aproximadamente 1 kHz a 7 kHz (1000 a 7000 vibraciones por segundo) que a los sonidos de muy baja o alta frecuencia. Por esta razón, los sonómetros suelen llevar un filtro cuya respuesta a la frecuencia se asemeja a la del oído humano. (Más adelante se habla de estos filtros.) Si se utiliza el «filtro de ponderación A», el nivel de presión sonora se da en unidades de dB(A) o dBA. El nivel de presión sonora en la escala dBA es fácil de medir y, por lo tanto, se utiliza ampliamente. Una de las razones por las que es diferente de la sonoridad es porque el filtro no responde de la misma manera que el oído. Para entender la sonoridad de un sonido, lo primero que hay que hacer es consultar algunas curvas que representan la respuesta en frecuencia del oído humano, que se dan a continuación. (Como alternativa, puedes medir tu propia respuesta auditiva). Otra razón es que el oído humano no es logarítmico.

Medidas logarítmicas

¿Por qué usamos decibelios? El oído es capaz de escuchar un rango muy grande de sonidos: la relación entre la presión sonora que causa daños permanentes por una corta exposición y el límite que los oídos (no dañados) pueden escuchar es más de un millón. Para tratar esta gama, las unidades logarítmicas son útiles: el logaritmo de un millón es 6, por lo que esta relación representa una diferencia de 120 dB. La audición no tiene una respuesta intrínsecamente logarítmica. (Las medidas logarítmicas también son útiles cuando un sonido aumenta o disminuye (brevemente) de forma exponencial en el tiempo. Esto ocurre en muchas aplicaciones que implican una ganancia proporcional o una pérdida proporcional.)

Los filtros utilizados para dBA y dB(C)

El filtro de nivel sonoro más utilizado es el de la escala A, que corresponde aproximadamente a la inversa de la curva de sonoridad de 40 dB (a 1 kHz). Con este filtro, el sonómetro es menos sensible a las frecuencias muy altas y muy bajas. Las mediciones realizadas en esta escala se expresan en dBA. La escala C varía poco a lo largo de varias octavas y, por tanto, sólo es adecuada para mediciones subjetivas de niveles sonoros moderados y altos. Las mediciones realizadas en esta escala se expresan en dB(C). También existe una escala de ponderación B (poco utilizada), intermedia entre la A y la C. La figura siguiente muestra la respuesta del filtro A (izquierda) y del filtro C, con ganancias en dB dadas con respecto a 1 kHz. (Para una introducción a los filtros, véase Filtros RC, integradores y diferenciadores).



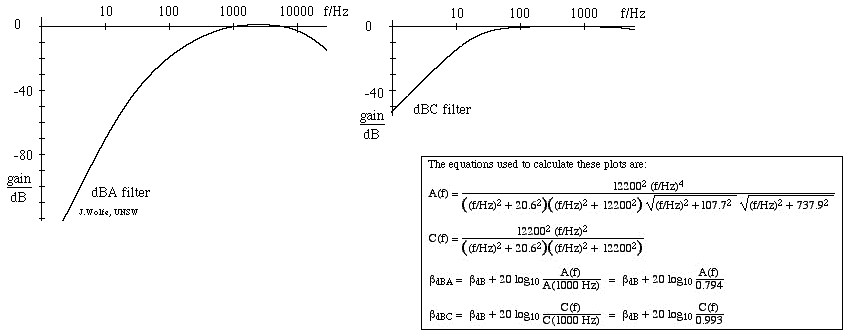
En los sitios de acústica musical y acústica del habla, trazamos los espectros sonoros en dB. La razón de esta práctica común es que el rango de presiones sonoras medidas es grande.

Las mediciones en dB(G) utilizan un filtro de banda estrecha que da una alta ponderación a las frecuencias entre 1 y 20 Hz, y una baja ponderación a las demás. Por lo tanto, da valores grandes para los sonidos e infrasonidos que no se pueden oír fácilmente. ISO 7196:1995

Altura, phons y sones, curvas de respuesta auditiva

El phon es una unidad que se relaciona con el dB por la respuesta en frecuencia medida psicofísicamente del oído. A 1 kHz, las lecturas en phons y dB son, por definición, las mismas. Para todas las demás frecuencias, la escala de phon se determina por los resultados de los experimentos en los que se pidió a los voluntarios que ajustaran la sonoridad de una señal a una frecuencia determinada hasta que juzgaran que su sonoridad era igual a la de una señal de 1 kHz. Para convertir de dB a phons, se necesita un gráfico de dichos resultados. Dicho gráfico depende del nivel de sonido: se vuelve más plano a niveles de sonido altos.

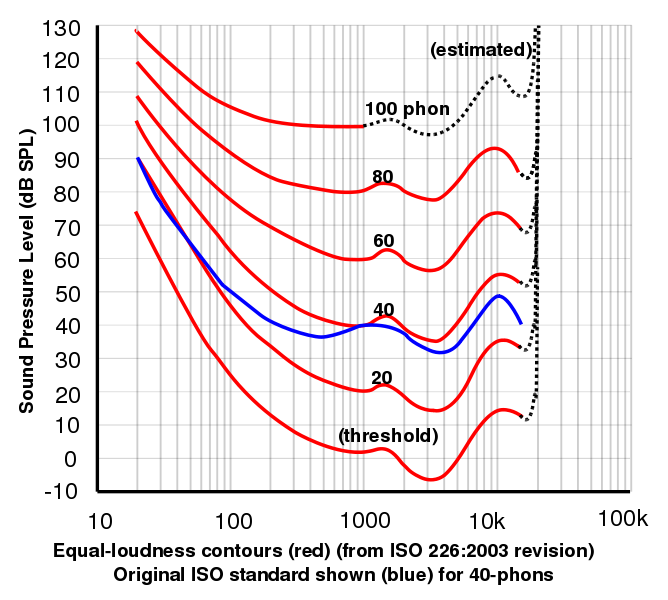
Este gráfico, cortesía de Lindosland, muestra los datos de 2003 de la Organización Internacional de Normalización para las curvas de igual intensidad sonora determinadas experimentalmente. Los gráficos de intensidad sonora igual en función de la frecuencia suelen denominarse genéricamente curvas de Fletcher-Munson por el trabajo original de Fletcher, H. y Munson, W.A. (1933) J.Acoust.Soc.Am. 6:59. Puede hacer sus propias curvas utilizando nuestro sitio de respuesta auditiva.

El tono se deriva de las mediciones psicofísicas que implican que los voluntarios ajusten los sonidos hasta que los juzguen como el doble de fuertes. Esto permite relacionar la intensidad percibida con los fonemas. Un sone equivale a 40 phons. Experimentalmente se ha comprobado que, por encima de 40 fones, un aumento de 10 dB en el nivel sonoro corresponde aproximadamente a una percepción del doble de volumen. Así que esa aproximación se utiliza en la definición del sone: 1 sone = 40 phon, 2 sone = 50 phon, 4 sone = 60 phon, etc.



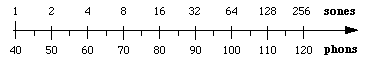
Esta relación implica que la sonoridad y la intensidad están relacionadas por una ley de potencia: la sonoridad en sones es proporcional a (intensidad)log 2 = (intensidad)0,3.

¿No sería estupendo poder convertir de dB (que se pueden medir con un instrumento) a sones (que aproximan la sonoridad percibida por las personas)? Esto se hace a veces mediante tablas que se pueden encontrar en los manuales de acústica. Sin embargo, si no te importa una aproximación bastante burda, puedes decir que la curva de ponderación A se aproxima a la respuesta en frecuencia del ser humano a niveles sonoros bajos y moderados, por lo que dB(A) es más o menos lo mismo que los sones, en un rango limitado de niveles bajos. Entonces se puede utilizar la relación logarítmica entre sones y phons descrita anteriormente.

Nivel de grabación y decibelios

Los medidores que miden el nivel de grabación o de salida en los equipos electrónicos de audio (mesas de mezclas, etc.) casi siempre registran el voltaje AC rms (ver enlaces para saber sobre AC y rms). Para una resistencia dada R, la potencia P es V2/R, por lo que
diferencia de nivel de tensión = 20 log (V2/V1) dB = 10 log (V22/V12) dB = 10 log (P2/P1) dB, o

nivel de tensión absoluto = 20 log (V/Vref)

donde Vref es una tensión de referencia. Entonces, ¿cuál es la tensión de referencia?

El nivel obvio a elegir es un voltio rms, y en este caso el nivel se escribe como dBV. Esto es racional, y también conveniente con las tarjetas analógico-digitales cuyo rango máximo es a menudo alrededor de un voltio rms. Así que uno tiene que recordar mantener el nivel en dBV negativo (menos de un voltio) para evitar recortar los picos de la señal, pero no demasiado negativo (por lo que su señal sigue siendo mucho mayor que el ruido de fondo).

A veces verá dBm. Esto solía significar decibelios de potencia eléctrica, con respecto a un milivatio, y a veces todavía lo hace. Sin embargo, es complicado por razones históricas. A mediados del siglo XX, muchas líneas de audio tenían una impedancia nominal de 600 Ω. Si la impedancia es puramente resistiva, y si estableces V2/600 Ω = 1 mW, entonces obtienes V = 0,775 voltios. Así que, siempre que estuvieras usando una carga de 600 Ω, 1 mW de potencia era 0 dBm, que era 0,775 V, por lo que calibrabas así tus medidores de nivel. El problema surgió porque, una vez que un medidor de nivel que mide la tensión está calibrado así, leerá 0 dBm a 0,775 V aunque no esté conectado a 600 Ω Así que, tal vez de forma ilógica, dBm significará a veces dB con respecto a 0,775 V. (Cuando era niño, las calculadoras eran caras, así que usaba la vieja regla de cálculo de papá, que tenía el factor 0,775 marcado en la ventana del cursor para facilitar esos cálculos).

¿Cómo convertir dBV o dBm en dB de nivel sonoro? No hay una forma sencilla. Depende de cómo conviertas la potencia eléctrica en potencia sonora. Incluso si su señal eléctrica está conectada directamente a un altavoz, la conversión dependerá de la eficiencia y la impedancia de su altavoz. Y, por supuesto, puede haber un amplificador de potencia y diversas complicaciones acústicas entre el lugar donde se miden los dBV en la mesa de mezclas y el lugar donde se encuentran sus oídos en el campo sonoro.

Intensidad, radiación y dB



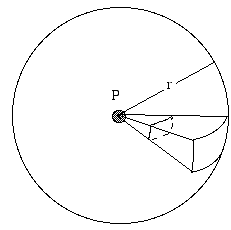
¿Cómo depende el nivel de sonido (o el nivel de la señal de radio, etc.) de la distancia a la fuente?

Una fuente que emite radiación por igual en todas las direcciones se llama isotrópica. Consideremos una fuente sonora aislada, alejada de cualquier superficie reflectante, tal vez un pájaro cantando en lo alto del aire. Imaginemos una esfera de radio r centrada en la fuente. La fuente emite una potencia total P, de forma continua. Esta potencia sonora se propaga y atraviesa la superficie de la esfera. Si la fuente es isotrópica, la intensidad I es la misma en toda esta superficie, por definición. La intensidad I se define como la potencia por unidad de superficie. La superficie de la esfera es 4πr2, por lo que la potencia (en nuestro ejemplo, la potencia sonora) que atraviesa cada metro cuadrado de superficie es, por definición:

I = P/4πr2.

Así vemos que, para una fuente isotrópica, la intensidad es inversamente proporcional al cuadrado de la distancia a la fuente:

I2/I1 = r12/r22.

Pero la intensidad es proporcional al cuadrado de la presión sonora, por lo que podríamos escribir igualmente:

p2/p1 = r1/r2.

Entonces, si duplicamos la distancia, reducimos la presión sonora en un factor 2 y la intensidad en un factor 4: es decir, reducimos el nivel sonoro en 6 dB. Si aumentamos r en un factor de 10, disminuimos el nivel en 20 dB, etc.

Sin embargo, hay que tener en cuenta que muchas fuentes no son isótropas, especialmente si la longitud de onda es menor o de un tamaño comparable al de la fuente. Además, las reflexiones suelen ser bastante importantes, sobre todo si el suelo está cerca, o si se está en interiores.

Presión, intensidad e impedancia específica

Para las ondas acústicas, la impedancia acústica específica z se define como la relación entre la presión acústica p y la velocidad media de las partículas u, debida al sonido ave, z = p/u . En Impedancia acústica, intensidad y potencia, mostramos cómo relacionar la presión acústica p y la intensidad I:
I = p2/z

Para el aire, la impedancia acústica específica z es 420 kg.s-1.m-2 = 420 Pa.s.m-1. Para el agua (dulce), la impedancia acústica específica del agua es de 1,48 MPa.s.m-1. Así que una onda sonora en el agua con la misma presión tiene una intensidad mucho menor que una en el aire.

dBi y la radiación que varía con la dirección

La radiación que varía con la dirección se llama anisotrópica. Para muchos casos en la comunicación, la radiación isotrópica es un desperdicio: para qué emitir una fracción sustancial de la potencia hacia arriba si el receptor está, como tú, relativamente cerca del nivel del suelo. Para el sonido de longitud de onda corta (incluyendo la mayor parte del rango importante para el habla), un megáfono puede ayudar a que su voz sea más anisotrópica. Para la radio, una amplia gama de diseños permite que las antenas sean altamente anisotrópicas tanto para la transmisión como para la recepción.

Así pues, cuando nos interesa la emisión en (o la recepción desde) una dirección concreta, queremos que la relación de intensidad medida en esa dirección, a una distancia determinada, sea mayor que la medida a la misma distancia desde un radiador isótropo (o recibida por un receptor isótropo). Esta relación se llama ganancia; exprese la relación en dB y tendrá la ganancia en dBi para ese radiador. Esta unidad se utiliza principalmente para las antenas, tanto de transmisión como de recepción, pero a veces se utiliza para las fuentes de sonido y los micrófonos direccionales.

Problemas de ejemplo

Unas cuantas personas han escrito pidiendo ejemplos en el uso de dB en los cálculos. Así que…
• A igualdad de condiciones, ¿cuánto más fuerte es el altavoz impulsado (en su rango lineal) por un amplificador de 100 W que por uno de 10 W?

  Las potencias difieren en un factor de diez, que, como vimos anteriormente, es de 10 dB. Todo lo demás igual aquí significa que las respuestas en frecuencia son iguales y que se utiliza la misma señal de entrada, etc. Por tanto, la dependencia de la frecuencia debería ser la misma. 10 dB corresponden a 10 fones. Para obtener una percepción del doble de volumen, se necesita un aumento de 10 fones. Por lo tanto, el altavoz accionado por el amplificador de 100 W tiene el doble de volumen que cuando es accionado por el de 10 W, suponiendo que se mantenga en el rango lineal y no distorsione o destruya el altavoz. (El amplificador de 100 W produce el doble de sonidos que el de 10 W.)

• Estoy de pie a una distancia R de una pequeña fuente de sonido (de tamaño mucho menor que R), a nivel del suelo al aire libre donde se pueden despreciar las reflexiones. El nivel sonoro es L. Si ahora me muevo a una distancia nR (n un número, y nR todavía mucho mayor que el tamaño de la fuente), ¿cuál será el nuevo nivel sonoro?

  En primer lugar, hay que tener en cuenta que es muy importante no tener en cuenta las reflexiones. Este cálculo no funcionará dentro de una sala, donde las reflexiones de la pared (que producen colectivamente reverberación) dificultan bastante el cálculo. Al aire libre, la intensidad del sonido es proporcional a 1/r2, donde r es la distancia a la fuente. (La constante de proporcionalidad depende de lo bien que refleje el suelo, y no nos concierne aquí, porque se cancelará aproximadamente en el cálculo, siempre que r sea razonablemente grande). Así, si aumentamos r de R a nR, disminuimos la intensidad de I a I/n 2.

  La diferencia en decibelios entre las dos señales de intensidad I 2 e I 1 se define arriba como

  ΔL = 10 log (I2/I1) = 10 log ((I/n 2)/I) = 10 log (1/n 2) = -10 log (n 2) = -20 log n.

  Por ejemplo, si n es 2 (es decir, si nos alejamos el doble), la intensidad se reduce en un factor de cuatro y el nivel sonoro cae de L a (L – 6dB).

• Si, en condiciones ideales de silencio, un joven puede escuchar un tono de 1 kHz a 0 dB emitido por un altavoz (¿tal vez un altavoz blando?), ¿en cuánto debe aumentarse la potencia del altavoz para elevar el sonido a 110 dB (un nivel peligrosamente alto, pero que permite sobrevivir)?

  La diferencia en decibelios entre las dos señales de potencia P2 y P1 se define arriba como

  ΔL = 10 log (P2/P1) dB por lo que, elevando 10 a la potencia de estas dos cantidades iguales:
  10L/10 = P2/P1 por lo que:
  P2/P1 = 10110/10 = 1011 = cien mil millones.

  que es una demostración de que el oído humano tiene un rango dinámico notablemente grande, quizás mayor que el del ojo.

• Un amplificador tiene una entrada de 10 mV y una salida de 2 V. Cuál es su ganancia de tensión en dB?

  La tensión, al igual que la presión, aparece elevada al cuadrado en las expresiones de potencia o intensidad. (La potencia disipada en una resistencia R es V2/R.) Así que, por convención, definimos:

  ganancia = 20 log (Vout/Vin)
  = 20 log (2V/10mV)
  = 46 dB

  (En los casos acústicos dados anteriormente, vimos que la relación de presión, expresada en dB, era la misma que la relación de potencia: esa era la razón del factor 20 al definir dB para la presión. Cabe señalar que, en el ejemplo de la ganancia de tensión, es poco probable que la ganancia de potencia del amplificador sea igual a la ganancia de tensión, que se define por la convención utilizada aquí. La potencia es proporcional al cuadrado de la tensión en una resistencia determinada. Sin embargo, las impedancias de entrada y salida de los amplificadores suelen ser bastante diferentes. Por ejemplo, un amplificador buffer o seguidor de emisor tiene una ganancia de tensión de aproximadamente 1, pero una gran ganancia de corriente).

• ¿Cuál es la diferencia, en dB, entre la irradiancia (intensidad de la luz) en la tierra (8,3 minutos luz del sol) y en Urano (160 minutos luz)?

  Al igual que el sonido, la intensidad de la luz isotrópica disminuye como r-2, por lo que la relación de intensidad es (160/8.3)2 = 20 log (160/8,3) = 26 dB.

Seguridad y salud laboral

Los diferentes países y provincias tienen, obviamente, diferentes leyes relativas a la exposición al ruido en el trabajo, que se aplican con diferente entusiasmo. Muchas de estas normativas tienen un límite de exposición al ruido continuo de 85 dB(A), para un turno de 8 horas. Por cada aumento de 3 dB, la exposición permitida se reduce a la mitad. Así, si trabajas en un club nocturno donde la música amplificada produce 100 dB(A) cerca de tus oídos, la exposición permitida es de 15 minutos. Existe un límite para los ruidos de impulso, como las armas de fuego o las herramientas que utilizan disparos explosivos. (Hay muchos documentos que aconsejan cómo reducir la exposición al ruido en la fuente (es decir, bajar el nivel de la música), entre la fuente y el oído (es decir, alejarse de los altavoces en un concierto) y en el oído (es decir, usar tapones o protectores auditivos industriales). La gestión del ruido y la protección de la audición en el trabajo es el código de prácticas en el estado de Nueva Gales del Sur, Australia (la dirección del autor).

Algunas preguntas frecuentes

• ¿Qué ruido hace un avión? ¿Un tren? ¿Una persona cantando? ¿Un perro ladrando? Una herramienta eléctrica? Las respuestas a esta pregunta varían considerablemente. Depende en gran medida de la distancia a la que te encuentres, de si estás en un lugar cerrado o no, de si hay reverberación, de la intensidad de la fuente concreta y de su espectro. Dar valores, sin ser muy específico sobre las condiciones, sería algo engañoso. Como el resto de esta página pretende ser fiable, dentro de lo que cabe, prefiero no dar valores aquí.
• ¿Cómo se «suman decibelios»?, es decir, ¿Qué nivel de sonido se obtiene al sumar el nivel a al nivel b? Si las fuentes son coherentes (lo que suele significar que, en última instancia, provienen de la misma fuente), entonces puede haber efectos de interferencia complicados. En la mayoría de los casos, cuando las fuentes son independientes, se pueden sumar las intensidades y luego convertirlas en decibelios. Sin embargo, si se dan los niveles de sonido en dB(A), no es tan fácil volver a la intensidad, y hay que saber algo sobre el espectro del sonido. Si conoces la distribución del sonido en diferentes bandas de frecuencia, puedes utilizar el applet de este enlace.
• Some of the questions on our FAQ in music acoustics relate to decibels, including
  • Why do the sounds of two musical instruments always reinforce, and never cancel out?
  • How much does one more violin add to the sound level of a section of n violins?
  • Does adding two equal sounds give an increase of 3 or 6 dB? Why?
  • What is the loudest sound?
  • Is there really no sound in space?

Related pages

• Measure your own hearing response
• Adding sound levels from incoherent sources
• What are interference beats and Tartini tones?
• FAQ in music acoustics
• Loudness and spectra: how spectral content and other features are related to loudness
• Formants: what are they? A discussion of the different meanings of this term
• Music acoustics home page
• Physclips: a multi-level, multimedia introduction to mechanics.
• A list of other educational web sites from this author.