Distribución marginal

Distribuciones de probabilidad > Distribución marginal

¿Qué es una distribución marginal?

Mira el vídeo o lee el artículo que aparece a continuación:

La definición técnica puede ser un poco alucinante de ver:

Definición de una distribución marginal = Si X e Y son variables aleatorias discretas y f (x,y) es el valor de
su distribución de probabilidad conjunta en (x,y), las funciones dadas por:
g(x) = Σy f (x,y) y h(y) = Σx f (x,y) son las distribuciones marginales de X e Y , respectivamente.

Si eres bueno con las ecuaciones, esto es probablemente todo lo que necesitas saber. Te dice cómo encontrar una distribución marginal. Pero si esa fórmula te da dolor de cabeza (¡como a la mayoría de la gente!), puedes usar una tabla de distribución de frecuencias para encontrar una distribución marginal.

Una distribución marginal recibe su nombre porque aparece en los márgenes de una tabla de distribución de probabilidad.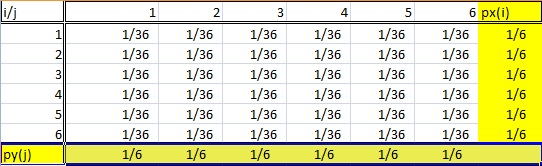

Por supuesto, no es tan simple como eso. No puedes mirar cualquier tabla de distribución de frecuencias y decir que la última columna (o fila) es una «distribución marginal». Las distribuciones marginales siguen un par de reglas:

• La distribución debe ser de datos bivariados. Bivariante es sólo otra forma de decir «dos variables», como X e Y. En la tabla anterior, las variables aleatorias i y j provienen de la tirada de dos dados.
• Una distribución marginal es aquella en la que sólo te interesa una de las variables aleatorias . En otras palabras, o bien X o bien Y. Si se observa la tabla de probabilidades anterior, las probabilidades de la suma de una variable aparecen en la fila inferior y las otras probabilidades de la suma aparecen en la columna de la derecha. Así que esta tabla tiene dos distribuciones marginales.

Diferencia entre la distribución marginal y la distribución condicional.

Una distribución condicional es aquella en la que sólo nos interesa una subpoblación concreta de todo nuestro conjunto de datos. En el ejemplo del lanzamiento de dados, esto podría ser «sacar un dos» o «sacar un seis». La imagen de abajo muestra dos subpoblaciones resaltadas (y por lo tanto, dos distribuciones condicionales).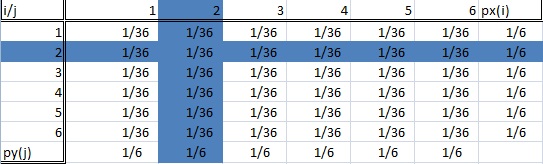

Cómo calcular la probabilidad de la distribución marginal

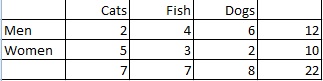
Pregunta de ejemplo: Calcule la distribución marginal de la preferencia de mascotas entre hombres y mujeres:
Solución:
Paso 1: Cuente el número total de personas. En este caso el total se da en la columna de la derecha (22 personas).
Paso 2: Cuente el número de personas que prefieren cada tipo de mascota y luego convierta la proporción en una probabilidad:
Personas que prefieren gatos: 7/22 = 0,32
Personas que prefieren peces: 7/22 = 0,32
Personas que prefieren perros: 8/22 = 0,36
Consejo: Puede comprobar su respuesta asegurándose de que todas las probabilidades suman 1.

Pregunta de ejemplo 2 (Sucesos mutuamente excluyentes): Si P(A) = 0,20, P(b) = 0,70, y ambos sucesos son mutuamente excluyentes, encuentre P(B’∩A), P(B’∩A’) y P(B∩A’).
Si no está familiarizado con esta notación, P(A’) significa «no A», o el complemento. P(B’∩A) significa «la intersección de no B y A»).

Respuesta:
Podrías calcular las probabilidades individualmente, pero son mucho más fáciles de calcular usando una tabla.

Paso 1: Rellena una tabla de frecuencias con la información dada. La probabilidad total debe ser igual a 1, por lo que puedes sumarla a los márgenes (totales) también. Una simple suma/álgebra rellena los espacios marginales. Por ejemplo, en la fila inferior 0,70 + x = 1,00 por lo que El total marginal para B’ debe ser 0,30.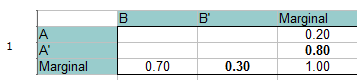

Paso 2: Añade 0 para la intersección de A y B, en la parte superior izquierda de la tabla. Puedes hacerlo porque A y B son mutuamente excluyentes y no pueden darse juntas.

Paso 3: Rellena el resto de los espacios en blanco usando suma/álgebra simple.

Lectura de la tabla (mira las intersecciones de las dos probabilidades indicadas):
P(B’∩A) = 0,20
P(B’∩A’) = 0,10
P(B∩A’) = 0,70.

Ejemplo de la pregunta 3 (Sucesos independientes): Si P(A) = 0,20, P(b) = 0,70, y ambos sucesos son independientes, encuentre P(B’∩A), P(B’∩A’) y P(B∩A’).

Respuesta: En esta ocasión, A y B son independientes, por lo que la probabilidad de que ambos ocurran al mismo tiempo es de 0,14 (P(A)*P(B) = 0,20 * 0,70 = 0,14). Este valor va en la parte superior izquierda (intersección de A y B). Rellena el resto de la tabla exactamente igual que en los pasos anteriores.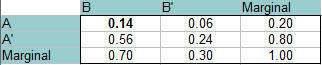

Lee las respuestas de la tabla (de las intersecciones de las dos probabilidades):
P(B’∩A): 0.06
P(B’∩A’): 0,24
P(B∩A’): 0,56.

Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Ratón, FL: CRC Press, pp. 536 y 571, 2002.
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, Nueva York.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2ª edición. McGraw-Hill Education

——————————————————————————

¿Necesitas ayuda con los deberes o con un examen? Con Chegg Study, puedes obtener soluciones paso a paso a tus preguntas de un experto en la materia. ¡Tus primeros 30 minutos con un tutor de Chegg son gratis!