¿Qué es el truco del kernel? Por qué es importante?
Cuando se habla de kernels en el aprendizaje automático, lo más probable es que lo primero que te venga a la mente sea el modelo de máquinas de vectores de soporte (SVM) porque el truco del kernel se utiliza ampliamente en el modelo SVM para salvar la linealidad y la no linealidad.
Para ayudarte a entender qué es un kernel y por qué es importante, voy a introducir primero los fundamentos del modelo SVM.
El modelo SVM es un modelo de aprendizaje automático supervisado que se utiliza principalmente para clasificaciones (¡pero también podría utilizarse para la regresión!). Aprende a separar diferentes grupos formando límites de decisión.

En el gráfico anterior, observamos que hay dos clases de observaciones: los puntos azules y los puntos morados. Hay muchas maneras de separar estas dos clases, como se muestra en el gráfico de la izquierda. Sin embargo, queremos encontrar el «mejor» hiperplano que pueda maximizar el margen entre estas dos clases, lo que significa que la distancia entre el hiperplano y los puntos de datos más cercanos de cada lado es la mayor. Dependiendo de en qué lado del hiperplano se sitúe un nuevo punto de datos, podríamos asignar una clase a la nueva observación.
Suena sencillo en el ejemplo anterior. Sin embargo, no todos los datos son linealmente separables. De hecho, en el mundo real, casi todos los datos están distribuidos aleatoriamente, lo que hace difícil separar linealmente las diferentes clases.

¿Por qué es importante utilizar el truco del núcleo?
Como puedes ver en la imagen anterior, si encontramos una forma de mapear los datos del espacio bidimensional al espacio tridimensional, podremos encontrar una superficie de decisión que divida claramente entre diferentes clases. Mi primera idea de este proceso de transformación de datos es mapear todos los puntos de datos a una dimensión más alta (en este caso, 3 dimensiones), encontrar el límite, y hacer la clasificación.
Eso suena bien. Sin embargo, cuando hay más y más dimensiones, los cálculos dentro de ese espacio se vuelven más y más costosos. Aquí es cuando entra en juego el truco del kernel. Nos permite operar en el espacio de características original sin calcular las coordenadas de los datos en un espacio de mayor dimensión.
Veamos un ejemplo:
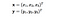
Aquí x e y son dos puntos de datos en 3 dimensiones. Supongamos que necesitamos mapear x e y en un espacio de 9 dimensiones. Tenemos que hacer los siguientes cálculos para obtener el resultado final, que es sólo un escalar. La complejidad computacional, en este caso, es O(n²).

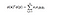
However, if we use the kernel function, which is denoted as k(x, y), instead of doing the complicated computations in the 9-dimensional space, we reach the same result within the 3-dimensional space by calculating the dot product of x -transpose and y. The computational complexity, in this case, is O(n).
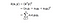
In essence, what the kernel trick does for us is to offer a more efficient and less expensive way to transform data into higher dimensions. With that saying, the application of the kernel trick is not limited to the SVM algorithm. Cualquier cálculo que implique los productos punto (x, y) puede utilizar el truco del kernel.
Diferentes funciones del kernel
Hay diferentes kernels. Los más populares son el kernel polinómico y el kernel de función de base radial (RBF).
«Intuitivamente, el kernel polinómico mira no sólo las características dadas de las muestras de entrada para determinar su similitud, sino también las combinaciones de éstas» (Wikipedia), como el ejemplo anterior. Con n características originales y d grados de polinomio, el kernel polinomial arroja n^d características expandidas.
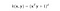
El kernel RBF también se llama kernel gaussiano. Hay un número infinito de dimensiones en el espacio de características porque puede ser expandido por la serie de Taylor. El parámetro γ define la influencia de un solo ejemplo de entrenamiento. Cuanto más grande es, más cerca deben estar otros ejemplos para ser afectados (documentación de sklearn).
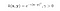
Hay diferentes opciones para las funciones del kernel en la biblioteca sklearn en Python. Incluso puedes construir un kernel personalizado si lo necesitas.
El final
El truco del kernel parece un plan «perfecto». Sin embargo, una cosa crítica a tener en cuenta es que cuando mapeamos los datos a una dimensión más alta, hay posibilidades de que podamos sobreajustar el modelo. Por lo tanto, la elección de la función kernel correcta (incluyendo los parámetros correctos) y la regularización son de gran importancia.
Si tienes curiosidad por saber qué es la regularización, he escrito un artículo hablando sobre mi forma de entenderla y lo puedes encontrar aquí.
Espero que disfrutes de este artículo. Como siempre, hazme saber si tienes alguna pregunta, comentario, sugerencia, etc. Gracias por leer 🙂