Solving the Königsberg Bridge Problem
This proof is accessible to ANYONE — no mathematics knowledge required! (perfect for if you are a bit bored and in isolation, like me right now!)
The Königsberg bridge problem shows the beauty of mathematics to transform the impossible to the obvious. It also gives an insight into the mind of the genius Leonhard Euler.

Stating the problem
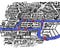
Have a look at the map above.
It’s a diagram of the rivers and bridges of Königsberg. The areas A, B, C and D are bits of land, joined by the bridges, but otherwise cut off from each other by water.
A map of the city is below. Puedes mirar cualquiera de los dos diagramas – ambos capturan los trozos de información clave: qué manchas de tierra están conectadas a qué otras manchas de tierra, y por cuántos puentes.
En lenguaje técnico, estamos representando esto como un gráfico. Las manchas de tierra son los vértices, y los puentes son las aristas. Pero eso no es importante.
El problema es si es posible encontrar una ruta que pase por cada puente exactamente una vez. Es decir, en nuestro paseo por la ciudad, queremos que nuestra ruta pase por todos los puentes, pero no puede cruzarlos dos veces, ni tres… Básicamente, si te encuentras en el mismo puente que antes, el camino no es válido. Si terminas tu paseo y hay un puente que no has cruzado, entonces tu ruta no era válida.
La solución
Considera cada blob de tierra. Cada puente está conectado a dos manchas de tierra (así es como funcionan los puentes). Resulta que cada blob de tierra tiene un número impar de puentes unidos.
Ahora, consideremos cómo sería un paseo válido.
Mientras vas caminando, anotas en un cuaderno cada vez que estás en un determinado blob de tierra. Por ejemplo, si empiezas en el extremo más meridional de la ciudad, lo anotas (haces una foto, compras un recuerdo…) y si te vuelves a encontrar allí, aumentas a dos la cuenta del sector sur.
Para cada mancha de tierra hay dos casos
(1) se trata de un sector de la ciudad en el que ni empezamos nuestro paseo, ni terminamos nuestro paseo allí
(2) se trata de un sector de la ciudad en el que o bien empezamos nuestro paseo, o bien terminamos nuestro paseo, o bien ambos.
Claramente, hay como máximo 2 sectores de la ciudad del segundo tipo. No podemos empezar en dos lugares a la vez, ni podemos terminar en dos lugares a la vez.
Como hay cuatro secciones de la ciudad, eso significa que hay al menos dos secciones de la ciudad, en nuestro paseo, en las que no terminamos ni empezamos. Escojamos uno de ellos.
Siempre que entramos en ese sector, gastamos un puente, y siempre que salimos de él usamos otro. Pero, ¡cada sector tiene un número impar de puentes unidos a él! Eso es una contradicción. Para ver por qué, recuerda que cada sector tiene o bien 3 puentes, o bien tiene 5 puentes adjuntos.
Si estamos en el sector una vez, sólo podemos utilizar dos de sus puentes. Si estamos en él dos veces, consumiríamos cuatro de sus puentes (o nos quedaríamos sin puentes, si sólo tuviera tres). Si entramos tres veces, necesitaríamos 6 puentes, que no podemos tener. Así que el requisito de que tanto entremos como salgamos de un sector de la ciudad que no sea nuestro punto de partida o de llegada contradice el hecho de que el número de puentes de conexión sea impar para cada sector.