Tipos de interpolación – Ventajas y desventajas
Métodos de interpolación
La interpolación es el proceso de utilizar puntos con valores conocidos o puntos de muestra para estimar valores en otros puntos desconocidos. Puede utilizarse para predecir valores desconocidos para cualquier dato geográfico puntual, como la elevación, las precipitaciones, las concentraciones químicas, los niveles de ruido, etc.
Los métodos de interpolación disponibles se enumeran a continuación.
Ponderación inversa de la distancia (IDW)
El interpolador de ponderación inversa de la distancia asume que cada punto de entrada tiene una influencia local que disminuye con la distancia. Pondera más los puntos más cercanos a la celda de procesamiento que los más alejados. Para determinar el valor de salida de cada lugar se puede utilizar un número determinado de puntos o todos los puntos dentro de un radio determinado. El uso de este método supone que la variable que se está mapeando disminuye su influencia con la distancia desde su ubicación muestreada.
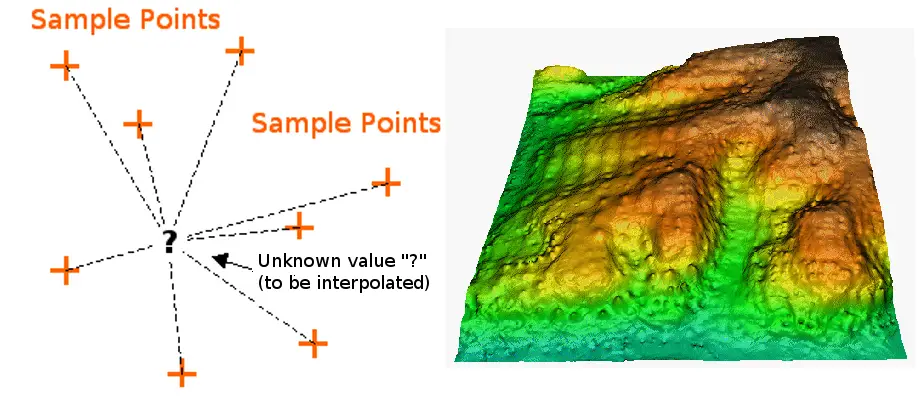
Interpolación IDW; Cortesía: QGIS
El algoritmo de ponderación inversa de la distancia (IDW) es efectivamente un interpolador de media móvil que suele aplicarse a datos muy variables. Para ciertos tipos de datos es posible volver al lugar de recogida y registrar un nuevo valor que es estadísticamente diferente de la lectura original, pero dentro de la tendencia general de la zona.
La superficie interpolada, estimada mediante una técnica de media móvil, es menor que el valor máximo local y mayor que el valor mínimo local.

Superficie interpolada IDW; Cortesía:ESRI
La interpolación IDW implementa explícitamente la suposición de que las cosas que están cerca son más parecidas que las que están más lejos. Para predecir un valor para cualquier lugar no medido, IDW utilizará los valores medidos que rodean el lugar de la predicción. Los valores medidos más cercanos al lugar de la predicción tendrán más influencia en el valor predicho que los más alejados. Así, IDW asume que cada punto medido tiene una influencia local que disminuye con la distancia. La función IDW debe utilizarse cuando el conjunto de puntos es lo suficientemente denso como para capturar la extensión de la variación local de la superficie necesaria para el análisis. La función IDW determina los valores de las celdas utilizando un conjunto de puntos de muestreo con ponderación lineal. Pondera más los puntos más cercanos a la ubicación de la predicción que los más lejanos, de ahí el nombre de distancia inversa ponderada.
La técnica IDW calcula un valor para cada nodo de la cuadrícula examinando los puntos de datos circundantes que se encuentran dentro de un radio de búsqueda definido por el usuario. Algunos o todos los puntos de datos pueden utilizarse en el proceso de interpolación. El valor del nodo se calcula promediando la suma ponderada de todos los puntos. Los puntos de datos que se encuentran progresivamente más lejos del nodo influyen en el valor calculado mucho menos que los que se encuentran más cerca del nodo.
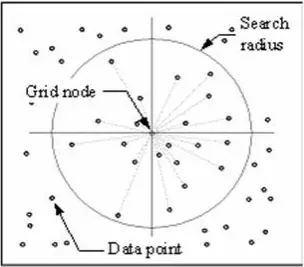
Se genera un radio alrededor de cada nodo de la cuadrícula del que se seleccionan los puntos de datos que se utilizarán en el cálculo. Options to control the use of IDW include power, search radius, fixed search radius, variable search radius and barrier.
Note: The optimal power (p) value is determined by minimizing the root mean square prediction error (RMSPE).
Advantages
- Can estimate extreme changes in terrain such as: Cliffs, Fault Lines.
- Dense evenly space points are well interpolated (flat areas with cliffs).
- Can increase or decrease amount of sample points to influence cell values.
Disadvantages
- Cannot estimate above maximum or below minimum values.
- Not very good for peaks or mountainous areas.
Natural Neighbour Inverse Distance Weighted (NNIDW)
Natural neighbor interpolation has many positive features, can be used for both interpolation and extrapolation, and generally works well with clustered scatter points. Otro método de media ponderada, la ecuación básica utilizada en la interpolación de vecinos naturales es idéntica a la utilizada en la interpolación IDW. Este método puede manejar eficazmente grandes conjuntos de datos de puntos de entrada. Cuando se utiliza el método del vecino natural, las coordenadas locales definen la cantidad de influencia que tendrá cualquier punto de dispersión en las celdas de salida.
El método del vecino natural es una técnica de estimación geométrica que utiliza regiones de vecindad natural generadas alrededor de cada punto del conjunto de datos.
Al igual que IDW, este método de interpolación es un método de interpolación de media ponderada. Sin embargo, en lugar de encontrar el valor de un punto interpolado utilizando todos los puntos de entrada ponderados por su distancia, la interpolación de Vecinos Naturales crea una Triangulación de Delauney de los puntos de entrada y selecciona los nodos más cercanos que forman un casco convexo alrededor del punto de interpolación, luego pondera sus valores por área proporcional. Este método es el más adecuado cuando los puntos de datos de la muestra están distribuidos con una densidad desigual. Es una buena técnica de interpolación de propósito general y tiene la ventaja de que no es necesario especificar parámetros como el radio, el número de vecinos o los pesos.

Identificación natural: Cortesía: ESRI
Esta técnica está diseñada para respetar los valores mínimos y máximos locales en el archivo de puntos y puede ajustarse para limitar los excesos de los valores altos locales y los excesos de los valores bajos locales. El método permite así la creación de modelos de superficie precisos a partir de conjuntos de datos que tienen una distribución espacial muy dispersa o muy lineal.
Ventajas
- Maneja un gran número de puntos de muestra de forma eficiente.
Spline
Spline estima los valores utilizando una función matemática que minimiza la curvatura global de la superficie, dando como resultado una superficie suave que pasa exactamente por los puntos de entrada.

Spline: Cortesía: ESRI
Conceptualmente, es análogo a doblar una lámina de goma para que pase por puntos conocidos minimizando la curvatura total de la superficie. Ajusta una función matemática a un número especificado de puntos de entrada más cercanos mientras pasa por los puntos de muestra. Este método es el mejor para superficies que varían suavemente, como la elevación, las alturas de la capa freática o las concentraciones de contaminación.
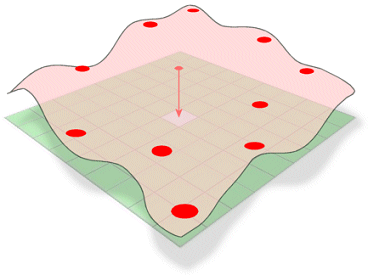
El método de interpolación Spline estima valores desconocidos doblando una superficie a través de valores conocidos.
Existen dos métodos de spline: regularizado y de tensión.
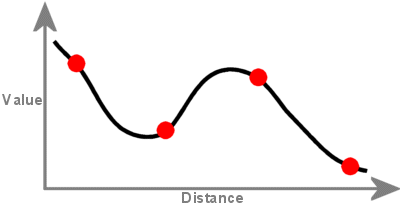
Una superficie creada con interpolación Spline pasa por cada punto de muestra y puede exceder el rango de valores del conjunto de puntos de muestra.
Aunque una spline de Tensión utiliza sólo la primera y segunda derivadas, incluye más puntos en los cálculos de Spline, lo que suele crear superficies más suaves pero aumenta el tiempo de cálculo.
Este método tira de una superficie sobre los puntos adquiridos dando como resultado un efecto estirado. Spline utiliza líneas curvas (método Líneas curvilíneas) para calcular los valores de las celdas.
Elegir un peso para las interpolaciones Spline
Spline regularizado: Cuanto mayor sea el peso, más suave será la superficie. Los pesos entre 0 y 5 son adecuados. Los valores típicos son 0, 0,001, 0,01, 0,1 y 0,5.
Spline de tensión: Cuanto mayor sea el peso, más gruesa será la superficie y más se ajustarán los valores al rango de datos de la muestra. Los valores de peso deben ser mayores o iguales a cero. Typical values are 0, 1, 5, and 10.
Advantages
- Useful for estimating above maximum and below minimum points.
- Creates a smooth surface effect.
Disadvantages
- Cliffs and fault lines are not well presented because of the smoothing effect.
- When the sample points are close together and have extreme differences in value, Spline interpolation doesn’t work as well. This is because Spline uses slope calculations (change over distance) to figure out the shape of the flexible rubber sheet.
Kriging
Kriging is a geostatistical interpolation technique that considers both the distance and the degree of variation between known data points when estimating values in unknown areas. A kriged estimate is a weighted linear combination of the known sample values around the point to be estimated.
Procedimiento de kriging que genera una superficie estimada a partir de un conjunto disperso de puntos con valores z. Kriging asume que la distancia o dirección entre los puntos de la muestra refleja una correlación espacial que puede utilizarse para explicar la variación en la superficie. La herramienta Kriging ajusta una función matemática a un número especificado de puntos, o a todos los puntos dentro de un radio especificado, para determinar el valor de salida de cada ubicación. Kriging es un proceso de varios pasos; incluye el análisis estadístico exploratorio de los datos, el modelado del variograma, la creación de la superficie y (opcionalmente) la exploración de una superficie de varianza. El kriging es más apropiado cuando se sabe que hay una distancia correlacionada espacialmente o un sesgo direccional en los datos. Se utiliza a menudo en la ciencia del suelo y la geología.
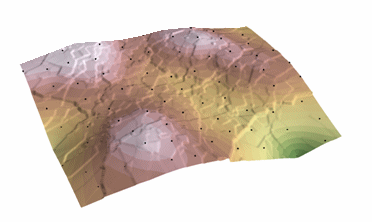
Kriging: Cortesía: ESRI
The predicted values are derived from the measure of relationship in samples using sophisticated weighted average technique. It uses a search radius that can be fixed or variable. The generated cell values can exceed value range of samples, and the surface does not pass through samples.
The Kriging Formula
Kriging is similar to IDW in that it weights the surrounding measured values to derive a prediction for an unmeasured location. The general formula for both interpolators is formed as a weighted sum of the data:
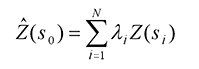
- where:
Z(si) = the measured value at the ith location
λi = an unknown weight for the measured value at the ith location
s0 = the prediction location
N = the number of measured values
In IDW, the weight, λi, depends solely on the distance to the prediction location. Sin embargo, con el método kriging, los pesos se basan no sólo en la distancia entre los puntos medidos y el lugar de predicción, sino también en la disposición espacial global de los puntos medidos. Para utilizar la disposición espacial en las ponderaciones, hay que cuantificar la autocorrelación espacial. Así, en el kriging ordinario, el peso, λi, depende de un modelo ajustado a los puntos medidos, de la distancia al lugar de predicción y de las relaciones espaciales entre los valores medidos en torno al lugar de predicción. En las siguientes secciones se analiza cómo se utiliza la fórmula general de kriging para crear un mapa de la superficie de predicción y un mapa de la precisión de las predicciones.
Tipos de Kriging
Kriging ordinario
El kriging ordinario asume el modelo
Z(s) = µ + ε(s),
donde µ es una constante desconocida. Una de las principales cuestiones relativas al kriging ordinario es si la suposición de una media constante es razonable. Sometimes there are good scientific reasons to reject this assumption. However, as a simple prediction method, it has remarkable flexibility.
Ordinary kriging can use either semivariograms or covariances, use transformations and remove trends, and allow for measurement error.
Simple Kriging
Simple kriging assumes the model
Z(s) = µ + ε(s),
where µ is a known constant.
Simple kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Universal Kriging
Universal kriging assumes the model
Z(s) = µ(s) + ε(s),
where µ(s) is some deterministic function.
Universal kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Kriging de indicadores
El kriging de indicadores asume el modelo
I(s) = µ + ε(s),
donde µ es una constante desconocida e I(s) es una variable binaria. La creación de datos binarios puede ser mediante el uso de un umbral para datos continuos, o puede ser que los datos observados sean 0 o 1. Por ejemplo, se puede tener una muestra que consiste en información sobre si un punto es un hábitat forestal o no forestal, donde la variable binaria indica la pertenencia a una clase. Utilizando variables binarias, el kriging indicador procede igual que el kriging ordinario.
El kriging indicador puede utilizar semivariogramas o covarianzas.
Kriging de probabilidad
El kriging de probabilidad asume el modelo
I(s) = I(Z(s) > ct) = µ1 + ε1(s)Z(s) = µ2 + ε2(s),
donde µ1 y µ2 son constantes desconocidas e I(s) es una variable binaria creada utilizando un indicador de umbral, I(Z(s) > ct). Nótese que ahora hay dos tipos de errores aleatorios, ε1(s) y ε2(s), por lo que hay autocorrelación para cada uno de ellos y correlación cruzada entre ellos. El kriging probabilístico trata de hacer lo mismo que el kriging de indicadores, pero utiliza el cokriging en un intento de hacer un mejor trabajo.
El kriging probabilístico puede utilizar semivariogramas o covarianzas, covarianzas cruzadas y transformaciones, pero no puede permitir el error de medición.
Estilo=»display:inline-block;width:468px;height:60px» data-ad-client=»ca-pub-7134201556760050″ data-ad-slot=»9271753327″>
Disjunctive Kriging
Disjunctive kriging asume el modelo
f(Z(s)) = µ1 + ε(s),
donde µ1 es una constante desconocida y f(Z(s)) es una función arbitraria de Z(s). Observe que puede escribir f(Z(s)) = I(Z(s) > ct), por lo que el kriging indicador es un caso especial del kriging disyuntivo. En Geostatistical Analyst, puede predecir el propio valor o un indicador con kriging disyuntivo.
En general, el kriging disyuntivo intenta hacer más que el kriging ordinario. Aunque las recompensas pueden ser mayores, también lo son los costes. Disjunctive kriging requires the bivariate normality assumption and approximations to the functions fi(Z(si)); the assumptions are difficult to verify, and the solutions are mathematically and computationally complicated.
Disjunctive kriging can use either semivariograms or covariances and transformations, but it cannot allow for measurement error.
Advantages
- Directional influences can be accounted for: Soil Erosion, Siltation Flow, Lava Flow and Winds.
- Exceeds the minimum and maximum point values
Disadvantages
- Does not pass through any of the point values and causes interpolated values to be higher or lower then real values.
** Para tener una visión profunda sobre el enfoque matemático en Kriging por favor haga clic en Kriging un método de interpolación.
PointInterp
Un método que es similar a IDW, la función PointInterp permite más control sobre el barrio de muestreo. La influencia de una muestra concreta en el valor de la celda de la cuadrícula interpolada depende de si el punto de la muestra se encuentra en la vecindad de la celda y de la distancia a la que se encuentra la celda interpolada. Los puntos fuera de la vecindad no tienen influencia.

PuntoInterp; Cortesía: ESRI
El valor ponderado de los puntos dentro del vecindario se calcula utilizando una interpolación ponderada de distancia inversa o interpolación de distancia exponencial inversa. Este método interpola un raster usando características de puntos pero permite diferentes tipos de vecindades. Las vecindades pueden tener formas como círculos, rectángulos, polígonos irregulares, anulaciones o cuñas.
Tendencia
La tendencia es un método estadístico que encuentra la superficie que se ajusta a los puntos de la muestra utilizando un ajuste de regresión de mínimos cuadrados. Se ajusta una ecuación polinómica a toda la superficie. El resultado es una superficie que minimiza la varianza de la superficie en relación con los valores de entrada. La superficie se construye de manera que para cada punto de entrada, el total de las diferencias entre los valores reales y los valores estimados (es decir, la varianza) sea lo más pequeño posible.

Tendencia; Courtsey:ESRI
Es un interpolador inexacto, y la superficie resultante rara vez pasa por los puntos de entrada. Sin embargo, este método detecta tendencias en los datos de la muestra y es similar a los fenómenos naturales que suelen variar suavemente.
Ventaja
- Las superficies de tendencia son buenas para identificar patrones de escala gruesa en los datos; la superficie interpolada rara vez pasa por los puntos de la muestra.
Topo a Raster
Al interpolar los valores de elevación para un raster, el método Topo a Raster impone restricciones que garantizan un modelo de elevación digital hidrológicamente correcto que contiene una estructura de drenaje conectada y representa correctamente las crestas y los arroyos de los datos de contorno de entrada. Utiliza una técnica de interpolación iterativa por diferencias finitas que optimiza la eficiencia computacional de la interpolación local sin perder la continuidad superficial de la interpolación global. Se ha diseñado específicamente para trabajar de forma inteligente con las entradas de contorno.
A continuación se muestra un ejemplo de una superficie interpolada a partir de puntos de elevación, curvas de nivel, líneas de corriente y polígonos de lago utilizando la interpolación Topo to Raster.
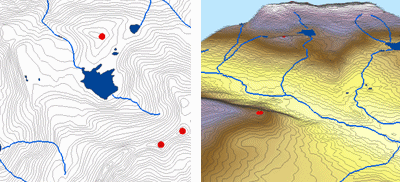
Topo a raster; Cortesía: ESRI
Topo to Raster es una herramienta especializada para crear superficies raster hidrológicamente correctas a partir de datos vectoriales de componentes del terreno como puntos de elevación, curvas de nivel, líneas de corriente, polígonos de lagos, puntos de hundimiento y polígonos de límites de áreas de estudio.
Densidad
Las herramientas de densidad (disponibles en ArcGIS) producen una superficie que representa la cantidad de algo por unidad de superficie. La herramienta de densidad es útil para crear superficies de densidad para representar la distribución de una población de vida silvestre a partir de un conjunto de observaciones, o el grado de urbanización de un área basado en la densidad de las carreteras.

Density Raster; Courtest: ERSI
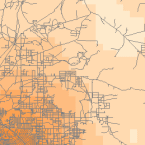
Density and Roads; Courtesy: ESRI
There are density tools for point and line features in ArcGIS.
Related Topics
- What is Interpolation ?
- Classification of Interpolation Techniques.
- Choosing the Right Interpolation Method