Ventaja comparativa

admin

Adam Smith aludió por primera vez al concepto de ventaja absoluta como base del comercio internacional en 1776, en La riqueza de las naciones:

Si un país extranjero puede suministrarnos una mercancía más barata de lo que nosotros mismos podemos fabricar, es mejor comprársela con una parte del producto de nuestra propia industria empleada de una manera en la que tengamos alguna ventaja. La industria general del país, estando siempre en proporción con el capital que la emplea, no se verá disminuida por ello, sino que sólo se dejará para encontrar la forma en que pueda ser empleada con la mayor ventaja.

Escribiendo varias décadas después de Smith en 1808, Robert Torrens articuló una definición preliminar de la ventaja comparativa como la pérdida por el cierre del comercio:

Si quiero saber la magnitud de la ventaja que supone para Inglaterra el hecho de dar a Francia cien libras de paño, a cambio de cien libras de encaje, tomo la cantidad de encaje que ha adquirido mediante esta transacción, y la comparo con la cantidad que podría haber adquirido, con el mismo gasto de trabajo y capital, fabricándolo en casa. El encaje que queda, más allá de lo que la mano de obra y el capital empleados en la tela, podrían haber fabricado en casa, es la cantidad de la ventaja que Inglaterra deriva del intercambio.

David Ricardo

En 1817, David Ricardo publicó lo que desde entonces se conoce como la teoría de la ventaja comparativa en su libro Sobre los principios de la economía política y la fiscalidad.

Ejemplo de RicardoEditar

Gráfico que ilustra el ejemplo de Ricardo:
En el caso I (rombos), cada país gasta 3600 horas para producir una mezcla de tela y vino.
En el caso II (cuadrados), cada país se especializa en su ventaja comparativa, lo que da lugar a una mayor producción total.

En un famoso ejemplo, Ricardo considera una economía mundial formada por dos países, Portugal e Inglaterra, cada uno de los cuales produce dos bienes de idéntica calidad. En Portugal, el país a priori más eficiente, es posible producir vino y tela con menos mano de obra que la que se necesitaría para producir las mismas cantidades en Inglaterra. Sin embargo, los costes relativos o el ranking de costes de producción de esos dos bienes difieren entre los países.

Horas de trabajo necesarias para producir una unidad
Produce
Country
 Cloth Wine
England 100 120
Portugal 90 80

In this illustration, England could commit 100 hours of labor to produce one unit of cloth, or produce 5/6 units of wine. Meanwhile, in comparison, Portugal could commit 100 hours of labor to produce 10/9 units of cloth, or produce 10/8 units of wine. So, Portugal possesses an absolute advantage in producing cloth due to more produced per hour (since 10/9 > 1), but England has a comparative advantage in producing cloth due to lower opportunity cost.

En otras palabras, si a un país le resulta más barato producir un bien en relación con otro, entonces tendrá una ventaja comparativa y un incentivo para producir más de ese bien que le resulta relativamente más barato que el otro -suponiendo que tenga una oportunidad ventajosa de comerciar en el mercado por el otro bien más difícil de producir. Del mismo modo, casi todo el mundo debería aprovechar la oportunidad de ofrecer en el mercado un bien que tiene una ventaja relativa en su producción.

En ausencia de comercio, Inglaterra requiere 220 horas de trabajo tanto para producir como para consumir una unidad de tela y de vino, mientras que Portugal requiere 170 horas de trabajo para producir y consumir las mismas cantidades. Inglaterra es más eficiente produciendo tela que vino, y Portugal es más eficiente produciendo vino que tela. Por tanto, si cada país se especializa en el bien para el que tiene una ventaja comparativa, la producción global de ambos bienes aumenta, ya que Inglaterra puede emplear 220 horas de trabajo para producir 2,2 unidades de tela, mientras que Portugal puede emplear 170 horas para producir 2,125 unidades de vino. Además, si ambos países se especializan de la forma anterior e Inglaterra intercambia una unidad de su paño por 5/6 a 9/8 unidades de vino de Portugal, entonces ambos países pueden consumir al menos una unidad de paño y otra de vino, quedando en cada país respectivo de 0 a 0,2 unidades de paño y de 0 a 0,125 unidades de vino para consumir o exportar. En consecuencia, tanto Inglaterra como Portugal pueden consumir más vino y paño en régimen de libre comercio que en autarquía.

Modelo ricardianoEditar

El modelo ricardiano es un modelo matemático de equilibrio general del comercio internacional. Aunque la idea del modelo ricardiano fue presentada por primera vez en el Ensayo sobre las ganancias (una versión de un solo producto) y luego en los Principios (una versión de varios productos) de David Ricardo, el primer modelo matemático ricardiano fue publicado por William Whewell en 1833. La primera prueba del modelo ricardiano fue realizada por G.D.A MacDougall, que se publicó en el Economic Journal de 1951 y 1952. En el modelo ricardiano, los patrones de comercio dependen de las diferencias de productividad.

La siguiente es una interpretación moderna típica del modelo ricardiano clásico. En aras de la simplicidad, utiliza notación y definiciones, como la de coste de oportunidad, no disponibles para Ricardo.

La economía mundial consta de dos países, el Interior y el Exterior, que producen vino y tela. La mano de obra, el único factor de producción, es móvil a nivel nacional pero no internacional; puede haber migración entre sectores pero no entre países. Denotamos la fuerza de trabajo en el País de Origen por L {\displaystyle \textstyle L}

\\Ntextstyle L

, la cantidad de mano de obra requerida para producir una unidad de vino en el Hogar por a L W {\displaystyle \textstyle a_{LW}}

textstyle a_{LW}}

, y la cantidad de trabajo requerida para producir una unidad de tela en el Hogar por un L C {\displaystyle \textstyle a_{LC}}

textstyle a_{LC}}

. La cantidad total de vino y tela producida en el Hogar son Q W {\displaystyle Q_{W}}

Q_{W} y Q C {{displaystyle Q_{C}}

Q_{C}

respectivamente. Denotamos las mismas variables para Foreign añadiendo un primo. Por ejemplo, a L W ′ {\displaystyle \textstyle a’_{LW}}

textstyle a'_{{LW}}'_{{LW}}

es la cantidad de trabajo necesaria para producir una unidad de vino en el Extranjero.

No sabemos si el Hogar puede producir tela utilizando menos horas de trabajo que el Extranjero. Es decir, no sabemos si a L C < a L C ′ {\displaystyle a_{LC}< a’_{LC}}.

a_{LC}}a'_{LC}}'_{{LC}}

. Del mismo modo, no sabemos si Home puede producir vino utilizando menos horas de trabajo. Sin embargo, suponemos que Home es relativamente más productivo que Foreign en la fabricación en tela frente al vino: a L C / a L C ′ < a L W / a L W ′ . {\displaystyle a_{LC}/a’_{LC}<a_{LW}/a’_{LW}.}

a_{{LC}}/a'_{{LC}}a_{{LW}}/a'_{{LW}}.'_{{LC}}<a_{{LW}}/a'_{{LW}}.

Equivalentemente, podemos suponer que el Hogar tiene una ventaja comparativa en el paño en el sentido de que tiene un coste de oportunidad del paño menor en términos de vino que el Extranjero:

a L C / a L W < a L C ′ / a L W ′ . {\displaystyle a_{LC}/a_{LW}<a’_{LC}/a’_{LW}.}

a_{{LC}}/a_{{LW}}a'_{{LC}}/a'_{LW}}.'_{{LC}}/a'_{{LW}}.

En ausencia de comercio, el precio relativo del paño y del vino en cada país está determinado únicamente por el coste laboral relativo de los bienes. Por lo tanto, el precio relativo de autarquía del paño es a L C / a L W {\displaystyle a_{LC}/a_{LW}}.

a_{LC}}/a_{LW}}

en el Hogar y a L C ′ / a L W ′ {\displaystyle a’_{LC}}/a’_{LW}}

en Extranjero. Con el libre comercio, el precio de la tela o del vino en cualquiera de los dos países es el precio mundial P C {displaystyle P_{C}}

P_{C}

o P W {{displaystyle P_{W}}

P_W

.

En lugar de considerar la demanda (u oferta) mundial de tela y vino, nos interesa la demanda relativa mundial (u oferta relativa) de tela y vino, que definimos como la relación entre la demanda (u oferta) mundial de tela y la demanda (u oferta) mundial de vino. In general equilibrium, the world relative price P C / P W {\displaystyle \textstyle P_{C}/P_{W}}

\textstyle P_{C}/P_{W}

will be determined uniquely by the intersection of world relative demand R D {\displaystyle \textstyle RD}

\textstyle RD

and world relative supply R S {\displaystyle \textstyle RS}

\textstyle RS

curves.

The demand for cloth relative to wine decreases with the relative price of cloth in terms of wine; the supply R S {\displaystyle RS}

RS

of cloth relative to wine increases with relative price. Two relative demand curves R D 1 {\displaystyle RD_{1}}

RD_{1}

and R D 2 {\displaystyle RD_{2}}

RD_{2} se dibujan con fines ilustrativos.

Suponemos que la curva de demanda relativa refleja los efectos de sustitución y es decreciente con respecto al precio relativo. El comportamiento de la curva de oferta relativa, sin embargo, merece un estudio más detallado. Recordando nuestro supuesto original de que el Hogar tiene una ventaja comparativa en telas, consideramos cinco posibilidades para la cantidad relativa de tela suministrada a un precio dado.

  • Si P C / P W = a L C / a L W < a L C ′ / a L W ′ {\displaystyle \textstyle P_{C}/P_{W}=a_{LC}/a_{LW}<a’_{LC}/a’_{LW}}
    texto P_{C}/P_{W}=a_{{LC}}/a'_{LW}}'_{{LC}}/a'_{{LW}}

    , entonces el Extranjero se especializa en el vino, para el salario P W ′ / a L W ′{displaystyle P’_{W}/a’_{LW}}

    P'_{W}/a'_{LW}}'_{W}/a'_{{LW}}

    en el sector vitivinícola es mayor que el salario P C ′ / a L C ′ {\displaystyle P’_{C}/a’_{LC}}

    P'_{C}/a'_{{LC}}'_{C}/a'_{{LC}}

    in the cloth sector. However, Home workers are indifferent between working in either sector. As a result, the quantity of cloth supplied can take any value.

  • If P C / P W < a L C / a L W < a L C ′ / a L W ′ {\displaystyle \textstyle P_{C}/P_{W}<a_{LC}/a_{LW}<a’_{LC}/a’_{LW}}
    \textstyle P_{C}/P_{W}a_{{LC}}/a_{{LW}}a'_{{LC}}/a'_{{LW}}'_{{LC}}/a'_{{LW}}

    , then both Home and Foreign specialize in wine, for similar reasons as above, and so the quantity of cloth supplied is zero.

  • If a L C / a L W < P C / P W < a L C ′ / a L W ′ {\displaystyle \textstyle a_{LC}/a_{LW}<P_{C}/P_{W}<a’_{LC}/a’_{LW}}
    textstyle a_{LC}}/a_{LW}}P_{C}/P_{LW}}a'_{LC}}/a'_{LW}}'_{{LC}}/a'_{{LW}}

    , entonces el Hogar se especializa en tela mientras que el Extranjero se especializa en vino. La cantidad de tela suministrada viene dada por la relación L / a L C L′ / a L W ′ {\displaystyle \textstyle {\frac {L/a_{LC}}{L’/a’_{LW}}}}

    textstyle {\frac {L/a_{LC}} de la producción mundial de tela a la producción mundial de vino.'/a'_{{LW}}}}

  • Si a L C / a L W < a L C ′ / a L W ′ < P C / P W {<a’_{LC}/a’_{LW}<P_{C}/P_{W}
    textstyle a_{LC}}/a_{LW}}a'_{LC}}/a'_{LW}}P_{C}/P_{W}'_{{LC}}/a'_{{LW}}<P_{C}/P_{W} , entonces tanto los nacionales como los extranjeros se especializan en tela. La cantidad de tela suministrada tiende a infinito a medida que la cantidad de vino suministrada se acerca a cero.

  • Si a L C / a L W < a L C ′ / a L W ′ = P C / P W {\displaystyle \textstyle a_{LC}/a_{LW}< a’_{LC}/a’_{LW}=P_{C}/P_{W}}
    texto a_{LC}}/a_{{LW}}a'_{LC}}/a'_{LW}}=P_{C}/P_{W}'_{{LC}}/a'_{{LW}}=P_{C}/P_{W} , entonces el Hogar se especializa en tela mientras que los trabajadores Extranjeros son indiferentes entre los sectores. De nuevo, la cantidad relativa de tela suministrada puede tomar cualquier valor.

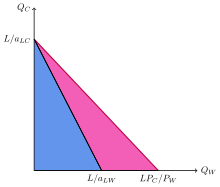    El triángulo azul representa las posibilidades originales de producción (y consumo) de Hogar. Mediante el comercio, Home también puede consumir paquetes en el triángulo rosa a pesar de enfrentarse a la misma frontera de posibilidades de producción.

    Mientras la demanda relativa sea finita, el precio relativo siempre está acotado por la desigualdad

    a L C / a L W ≤ P C / P W ≤ a L C ′ / a L W ′ . {\displaystyle a_{LC}/a_{LW}}leq {P_{C}/P_{W}}leq {a’_{LC}/a’_{LW}}.}

    a_{LC}/a_{{LW}}leq {P_{C}/P_{W}}leq {a'_{LC}}/a'_{LW}}.'_{{LC}}/a'_{{LW}}}.

    En la autarquía, el Hogar se enfrenta a una restricción de producción de la forma

    a L C Q C + a L W Q W ≤ L , {\displaystyle a_{LC}Q_{C}+a_{LW}Q_{W}leq L,}

    a_{LC}Q_{C}+a_{LW}Q_{W}leq L,

    De lo que se deduce que el consumo de ropa del Hogar en la frontera de posibilidades de producción es

    Q C = L / a L C – ( a L W / a L C ) Q W {\displaystyle Q_{C}=L/a_{LC}-(a_{LW}/a_LC})Q_{W}}

    Q_{C}=L/a_{{LC}}-(a_{{LW}}/a_{{LC}})Q_{W}

    .

    Con el libre comercio, Hogar produce exclusivamente telas, una cantidad de las cuales exporta a cambio de vino a la tasa vigente. Por lo tanto, el consumo global de Home está ahora sujeto a la restricción

    a L C Q C + a L C ( P W / P C ) Q W ≤ L {{displaystyle a_{LC}Q_{C}+a_{LC}(P_{W}/P_{C})Q_{W}}leq L}.

    a_{LC}Q_{C}+a_{LC}(P_{W}/P_{C})Q_{W}leq L

    mientras que su consumo de ropa en la frontera de posibilidades de consumo de consumo viene dado por

    Q C = L / a L C – ( P W / P C ) Q W ≥ L / a L C – ( a L W / a L C ) Q W {\displaystyle Q_{C}=L/a_{LC}-(P_{W}/P_{C})Q_{W}\geq L/a_{LC}-(a_{LW}/a_{LC})Q_{W}}

    Q_{C}=L/a_{{LC}}-(P_{W}/P_{C})Q_{W}\geq L/a_{{LC}}-(a_{{LW}}/a_{{LC}})Q_{W}

    .

    Un argumento simétrico es válido para el extranjero. Por tanto, al comerciar y especializarse en un bien para el que tiene una ventaja comparativa, cada país puede ampliar sus posibilidades de consumo. Los consumidores pueden elegir entre paquetes de vino y tela que no podrían haber producido ellos mismos en economías cerradas.

    Hay otra forma de demostrar la teoría de la ventaja comparativa, que requiere menos supuestos que la prueba detallada anteriormente, y en particular no requiere que los salarios por hora sean iguales en ambas industrias, ni requiere ningún equilibrio entre la oferta y la demanda en el mercado. Dicha prueba puede extenderse a situaciones con muchos bienes y muchos países, rendimientos no constantes y más de un factor de producción.

    Términos de intercambioEditar

    Los términos de intercambio son la tasa a la que se podría intercambiar un bien por otro. Si ambos países se especializan en el bien para el que tienen una ventaja comparativa entonces el comercio, los términos de intercambio para un bien (que beneficia a ambas entidades) caerá entre los costos de oportunidad de cada entidad. En el ejemplo anterior una unidad de tela se comerciaría por entre 5 6 {\displaystyle {\frac {5}{6}}.

    {\frac 56}

    unidades de vino y 9 8 {\displaystyle {\frac {9}{8}}

    {\frac 98}

    unidades de vino.