Calculatrice d’énergie potentielle gravitationnelle
Utilisation de la calculatrice
Cette calculatrice d’EPG trouvera la variable manquante dans l’équation de physique de l’énergie potentielle gravitationnelle, lorsque trois des variables sont connues.
Où :
- PEg ou PE = énergie potentielle gravitationnelle
- m = masse d’un objet
- g = accélération due à la gravité
- h = hauteur de l’objet
Qu’est-ce que l’énergie potentielle gravitationnelle (EPG)
L’énergie potentielle est l’énergie stockée d’un objet étant donné sa position par rapport à un corps. L’énergie potentielle gravitationnelle est un type d’énergie potentielle et est égale au produit de la masse de l’objet (m), de l’accélération due à la gravité (g) et de la hauteur de l’objet (h) en tant que distance par rapport à la surface du sol (le corps).
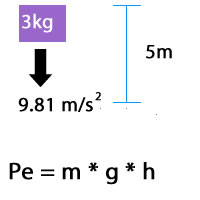
Dans cet exemple, une masse de 3 kilogrammes, à une hauteur de 5 mètres, alors qu’elle est agitée par la gravité terrestre, aurait 147,15 Joules d’énergie potentielle, PE = 3kg * 9.81 m/s2 * 5m = 147,15 J.
9,81 mètres par seconde au carré (ou plus précisément 9,80665 m/s2) est largement accepté parmi les scientifiques comme une valeur moyenne de travail pour la force gravitationnelle de la Terre. Ce chiffre est basé sur une mesure de la gravité au niveau de la mer à une latitude de 45°.
- À des altitudes plus élevées, la gravité diminue légèrement.
- L’effet de la latitude sur la force gravitationnelle est pertinent car la gravité augmente avec la distance à l’équateur. À l’équateur, la gravité de la Terre est de 9,780 m/s2 et aux pôles, elle est de 9,832 m/s2 (source : CRC Handbook of Chemistry and Physics).
L’accélération gravitationnelle (à trois chiffres significatifs) pour les autres planètes et corps du système solaire est la suivante :