dB : Qu’est-ce qu’un décibel ?

octobre 17, 2021admin

Pression sonore, niveau sonore et dB. Le son est généralement mesuré avec des microphones et ils répondent proportionnellement à la pression acoustique, p. Or la puissance dans une onde sonore, toutes choses égales par ailleurs, va comme le carré de la pression. (De même, la puissance électrique dans une résistance est égale au carré de la tension). Le logarithme de x2 est juste 2 log x, ce qui introduit un facteur de 2 lorsque nous convertissons les rapports de pression en décibels. La différence de niveau de pression acoustique entre deux sons de p1 et p2 est donc de :

20 log (p2/p1) dB = 10 log (p22/p12) dB = 10 log (P2/P1) dB (tout au long, le logarithme est en base 10).

Que se passe-t-il quand on divise par deux la puissance sonore ? Le log de 2 est 0,3010, donc le log de 1/2 est -0,3, en bonne approximation. Donc, si vous divisez la puissance par deux, vous réduisez la puissance et le niveau sonore de 3 dB. Divisez-la à nouveau par deux (jusqu’à 1/4 de la puissance initiale) et vous réduisez le niveau de 3 dB supplémentaires. Si vous continuez à diviser la puissance par deux, vous obtenez ces rapports.

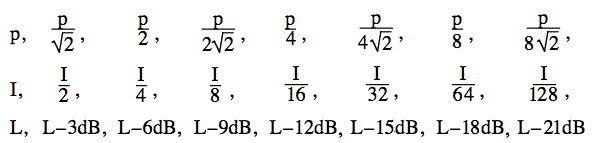
exemples de dB, de rapports de pression et de

Que se passe-t-il si j’ajoute deux sons identiques ? Est-ce que je double l’intensité (augmentation de 3 dB) ? Ou est-ce que je double la pression (augmentation de 6 dB) ? Cette question fréquemment posée est un peu subtile, c’est pourquoi elle est abordée ici dans notre FAQ.

Fichiers sonores pour montrer la taille d’un décibel

Nous avons vu plus haut que diviser la puissance par deux réduit la pression acoustique de √2 et le niveau sonore de 3 dB. C’est ce que nous avons fait dans le premier graphique et le fichier sonore ci-dessous.

Le premier échantillon de son est un bruit blanc (un mélange d’une large gamme de fréquences audibles, analogue à la lumière blanche, qui est un mélange de toutes les fréquences visibles). Le deuxième échantillon est le même bruit, avec une tension réduite d’un facteur √2. Or 1/√2 vaut environ 0,7, donc -3 dB correspond à une réduction de la tension ou de la pression à 70% de sa valeur d’origine. La ligne verte montre la tension en fonction du temps. La ligne rouge montre une décroissance exponentielle continue en fonction du temps. Notez que la tension chute de 50% pour chaque deuxième échantillon.

Notez également qu’un doublement de la puissance ne fait pas une énorme différence au niveau de l’intensité sonore. Nous en reparlerons plus loin, mais c’est une chose utile à retenir pour choisir un équipement de reproduction sonore. wav

Fichiers sonores et animation par John Tann et George Hatsidimitris.

Quelle est la taille d’un décibel ? Dans la série suivante, les échantillons successifs sont réduits d’un seul décibel.

Un décibel est du même ordre que la différence juste perceptible (JND) pour le niveau sonore. En écoutant ces fichiers, vous remarquerez que le dernier est plus silencieux que le premier, mais il est plutôt moins clair à l’oreille que le deuxième de toute paire est plus silencieux que son prédécesseur. 10*log10(1,26) = 1, donc pour augmenter le niveau sonore de 1 dB, il faut augmenter la puissance de 26%, ou la tension de 12%.

wav

Et si la différence est inférieure à un décibel ? Les niveaux sonores sont rarement indiqués avec des décimales. La raison en est que les niveaux sonores qui diffèrent de moins de 1 dB sont difficiles à distinguer, comme le montre l’exemple suivant.(Cela fait du dB une unité de taille pratique.)

Pas de 0,3 dB. Vous pouvez remarquer que le dernier est plus silencieux que le premier, mais il est difficile de remarquer la différence entre les paires successives. 10*log10(1,07) = 0,3, donc pour augmenter le niveau sonore de 0,3 dB, il faut augmenter la puissance de 7%, ou la tension de 3,5%.

wav

Niveaux de référence normalisés. (niveau sonore « absolu »)

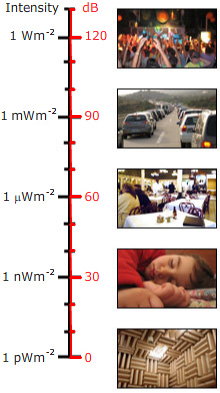échelle des décibels avec quelques exemples approximatifs

Donc, si vous lisez un niveau de pression acoustique de 86 dB, cela signifie que

20 log (p2/pref) = 86 dB

où pref est la pression acoustique du niveau de référence, et p2 celle du son en question. Divisez les deux côtés par 20 :

log (p2/pref) = 4,3

p2/pref = 104,3

4 est le logarithme de 10 mille, 0,3 est le logarithme de 2. Ce son a donc une pression acoustique 20 mille fois supérieure à celle du niveau de référence (p2/pref = 20 000) ou une intensité 400 millions de fois supérieure à l’intensité de référence. 86 dB est un son fort mais non dangereux – à condition que l’exposition soit brève.

Que signifie 0 dB ? Ce niveau apparaît lorsque l’intensité mesurée est égale au niveau de référence, c’est-à-dire qu’il s’agit du niveau sonore correspondant à 0,02 mPa. Dans ce cas, nous avons

niveau sonore = 20 log (pmesuré/pref) = 20 log 1 = 0 dB

Rappelez-vous que les décibels mesurent un rapport. On obtient 0 dB lorsqu’on prend le logarithme d’un rapport de 1 (log 1 = 0). Ainsi, 0 dB ne signifie pas l’absence de son, mais un niveau sonore où la pression acoustique est égale à celle du niveau de référence. Il s’agit d’une pression faible, mais pas nulle. Il est également possible d’avoir des niveaux sonores négatifs : – 20 dB signifierait un son dont la pression est 10 fois plus petite que la pression de référence, c’est-à-dire 2 μPa.

Toutes les pressions sonores ne sont pas également fortes. Cela s’explique par le fait que l’oreille humaine ne répond pas de la même manière à toutes les fréquences : nous sommes beaucoup plus sensibles aux sons situés dans la gamme de fréquences d’environ 1 kHz à 7 kHz (1000 à 7000 vibrations par seconde) qu’aux sons de très basse ou haute fréquence. C’est pourquoi les sonomètres sont généralement équipés d’un filtre dont la réponse à la fréquence ressemble un peu à celle de l’oreille humaine. (Plus d’informations sur ces filtres ci-dessous.) Si le « filtre de pondération A » est utilisé, le niveau de pression acoustique est donné en unités de dB(A) ou dBA. Le niveau de pression acoustique sur l’échelle dBA est facile à mesurer et est donc largement utilisé. L’une des raisons pour lesquelles il est différent de la sonie est que le filtre ne répond pas de la même manière que l’oreille. Pour comprendre l’intensité sonore d’un son, la première chose à faire est de consulter quelques courbes représentant la réponse en fréquence de l’oreille humaine, données ci-dessous. (Vous pouvez également mesurer votre propre réponse auditive.) Une autre raison est que l’audition humaine n’est pas logarithmique.

Mesures logarithmiques

Pourquoi utilisons-nous les décibels ? L’oreille est capable d’entendre une très large gamme de sons : le rapport entre la pression acoustique qui provoque des dommages permanents à la suite d’une courte exposition et la limite que les oreilles (non endommagées) peuvent entendre est supérieur à un million. Pour traiter une telle gamme, les unités logarithmiques sont utiles : le logarithme d’un million est 6, ce rapport représente donc une différence de 120 dB. L’audition n’est pas intrinsèquement logarithmique en réponse. (Les mesures logarithmiques sont également utiles lorsqu’un son augmente ou diminue (brièvement) de manière exponentielle dans le temps. Cela se produit dans de nombreuses applications impliquant un gain proportionnel ou une perte proportionnelle.)

Les filtres utilisés pour les dBA et les dB(C)

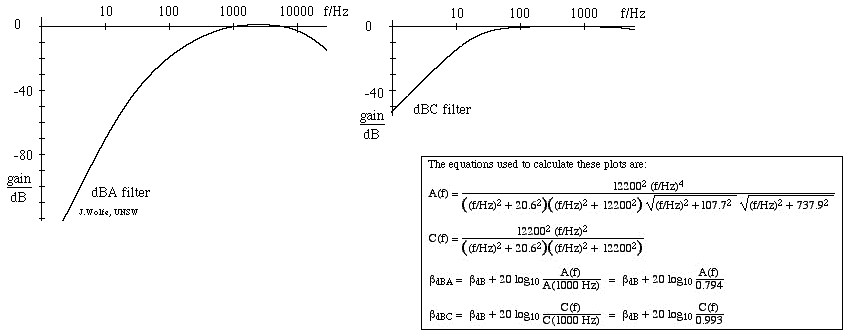
Sur les sites d’acoustique musicale et d’acoustique vocale, nous traçons les spectres sonores en dB. Cette pratique courante s’explique par le fait que la gamme des pressions sonores mesurées est large.

Les mesures en dB(G) utilisent un filtre à bande étroite qui donne une forte pondération aux fréquences comprises entre 1 et 20 Hz, et une faible pondération aux autres. Elle donne donc des valeurs importantes pour les sons et les infrasons qui ne sont pas facilement audibles. ISO 7196:1995

Loudness, phons et sones, courbes de réponse auditive

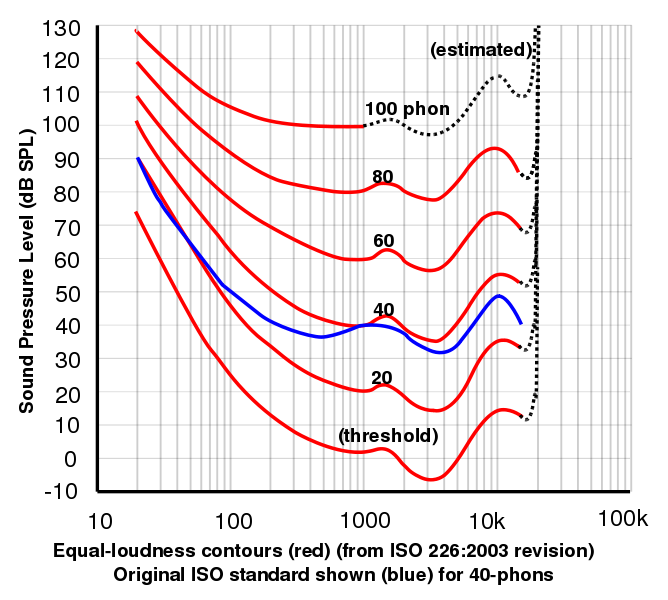
Courbes d'égale intensité sonore de l'ISO 226:2003

Ce graphique, gracieuseté de Lindosland, présente les données 2003 de l’Organisation internationale de normalisation pour les courbes d’égale intensité sonore déterminées expérimentalement. Les courbes d’intensité sonore égale en fonction de la fréquence sont souvent appelées courbes de Fletcher-Munson, d’après les travaux originaux de Fletcher, H. et Munson, W.A. (1933) J.Acoust.Soc.Am. 6:59. Vous pouvez réaliser vos propres courbes en utilisant notre site sur les réponses auditives.

Le sone est dérivé de mesures psychophysiques qui impliquaient des volontaires ajustant les sons jusqu’à ce qu’ils les jugent deux fois plus forts. Cela permet de faire le lien entre la sonie perçue et les sones. Un sone est défini comme étant égal à 40 phons. On a constaté expérimentalement qu’au-delà de 40 phons, une augmentation de 10 dB du niveau sonore correspond approximativement à un doublement de l’intensité perçue. Cette approximation est donc utilisée dans la définition du sone : 1 sone = 40 phons, 2 sone = 50 phons, 4 sone = 60 phons, etc.

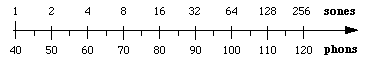
Cette relation implique que la sonie et l’intensité sont liées par une loi de puissance : la sonie en sone est proportionnelle à (intensité)log 2 = (intensité)0,3.

Ne serait-il pas formidable de pouvoir convertir les dB (qui peuvent être mesurés par un instrument) en sones (qui représentent approximativement l’intensité sonore telle que perçue par les gens) ? Cela se fait parfois à l’aide de tableaux que l’on trouve dans les manuels d’acoustique. Cependant, si vous n’avez pas peur d’une approximation assez grossière, vous pouvez dire que la courbe de pondération A se rapproche de la réponse en fréquence humaine à des niveaux sonores faibles à modérés, de sorte que dB(A) est très approximativement identique à phons, sur une gamme limitée de faibles niveaux. On peut alors utiliser la relation logarithmique entre sones et phons décrite ci-dessus.

Niveau d’enregistrement et décibels

niveau de tension absolu = 20 log (V/Vref)

où Vref est une tension de référence. Quelle est donc cette tension de référence ?

Le niveau évident à choisir est un volt rms, et dans ce cas le niveau est écrit en dBV. C’est rationnel, et aussi pratique avec les cartes analogiques-numériques dont la gamme maximale est souvent d’environ un volt rms. Il faut donc se rappeler de garder le niveau en dBV négatif (moins d’un volt) pour éviter d’écrêter les pics du signal, mais pas trop négatif (pour que votre signal soit encore beaucoup plus grand que le bruit de fond).

Parfois, vous verrez des dBm. Cela signifiait autrefois des décibels de puissance électrique, par rapport à un milliwatt, et c’est encore parfois le cas. Cependant, c’est compliqué pour des raisons historiques. Au milieu du vingtième siècle, de nombreuses lignes audio avaient une impédance nominale de 600 Ω. Si l’impédance est purement résistive, et si vous définissez V2/600 Ω = 1 mW, alors vous obtenez V = 0,775 volt. Donc, à condition que vous utilisiez une charge de 600 Ω, 1 mW de puissance correspondait à 0 dBm, soit 0,775 V, et vous avez donc étalonné vos indicateurs de niveau de cette façon. Le problème est apparu parce que, une fois qu’un mesureur de niveau qui mesure la tension est calibré de cette façon, il lira 0 dBm à 0,775 V même s’il n’est pas connecté à 600 Ω Donc, peut-être de façon illogique, dBm signifiera parfois dB par rapport à 0,775 V. (Quand j’étais un garçon, les calculatrices étaient chères, donc j’utilisais la vieille règle à calcul de papa, qui avait le facteur 0,775 marqué sur la fenêtre du curseur pour faciliter de tels calculs).

Comment convertir des dBV ou des dBm en dB de niveau sonore ? Il n’y a pas de méthode simple. Cela dépend de la façon dont vous convertissez la puissance électrique en puissance sonore. Même si votre signal électrique est connecté directement à un haut-parleur, la conversion dépendra de l’efficacité et de l’impédance de votre haut-parleur. Et bien sûr, il peut y avoir un amplificateur de puissance, et diverses complications acoustiques entre l’endroit où vous mesurez le dBV sur la table de mixage et celui où se trouvent vos oreilles dans le champ sonore.

Intensité, rayonnement et dB

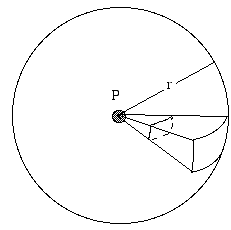
esquisse d'un rayonnement à symétrie sphérique

Une source qui émet un rayonnement de manière égale dans toutes les directions est dite isotrope. Considérons une source sonore isolée, loin de toute surface réfléchissante – peut-être un oiseau chantant haut dans les airs. Imaginez une sphère de rayon r, centrée sur la source. La source émet une puissance totale P, en continu. Cette puissance sonore se propage et traverse la surface de la sphère. Si la source est isotrope, l’intensité I est la même partout sur cette surface, par définition. L’intensité I est définie comme la puissance par unité de surface. La surface de la sphère est de 4πr2, donc la puissance (dans notre exemple, la puissance sonore) traversant chaque mètre carré de surface est, par définition :

I = P/4πr2.

On voit donc que, pour une source isotrope, l’intensité est inversement proportionnelle au carré de la distance à la source :

I2/I1 = r12/r22.

Mais l’intensité est proportionnelle au carré de la pression acoustique, donc on pourrait également écrire :

p2/p1 = r1/r2.

Donc, si nous doublons la distance, nous réduisons la pression acoustique d’un facteur 2 et l’intensité d’un facteur 4 : autrement dit, nous réduisons le niveau sonore de 6 dB. Si nous augmentons r d’un facteur 10, nous diminuons le niveau de 20 dB, etc.

Avertissez-vous toutefois que de nombreuses sources ne sont pas isotropes, surtout si la longueur d’onde est inférieure à la source ou d’une taille comparable à celle-ci. De plus, les réflexions sont souvent assez importantes, surtout si le sol est proche, ou si vous êtes à l’intérieur.

Pression, intensité et impédance spécifique

I = p2/z

Pour l’air, l’impédance acoustique spécifique z est de 420 kg.s-1.m-2 = 420 Pa.s.m-1. Pour l’eau (douce), l’impédance acoustique spécifique de l’eau est de 1,48 MPa.s.m-1. Donc une onde sonore dans l’eau avec la même pression a une intensité beaucoup plus faible que dans l’air.

dBi et rayonnement qui varie avec la direction

Donc, quand on s’intéresse à l’émission dans (ou à la réception depuis) une direction particulière, on veut que le rapport de l’intensité mesurée dans cette direction, à une distance donnée, soit plus élevé que celui mesuré à la même distance depuis un radiateur isotrope (ou reçu par un récepteur isotrope). Ce rapport s’appelle le gain ; exprimez le rapport en dB et vous avez le gain en dBi pour ce radiateur. Cette unité est principalement utilisée pour les antennes, que ce soit en émission ou en réception, mais elle est parfois utilisée pour les sources sonores et les microphones directionnels.

Problèmes d’exemples

Toutes choses égales par ailleurs, de combien est plus fort le haut-parleur piloté (dans sa gamme linéaire) par un amplificateur de 100 W que par un amplificateur de 10 W ?
Les puissances diffèrent d’un facteur dix, ce qui, comme nous l’avons vu plus haut, représente 10 dB. Toutes choses égales par ailleurs signifie ici que les réponses en fréquence sont égales et que l’on utilise le même signal d’entrée, etc. La dépendance en fréquence devrait donc être la même. 10 dB correspond à 10 phons. Pour obtenir un doublement perçu de l’intensité sonore, vous avez besoin d’une augmentation de 10 phons. Ainsi, le haut-parleur alimenté par un amplificateur de 100 W est deux fois plus fort que lorsqu’il est alimenté par un amplificateur de 10 W, en supposant que vous restiez dans la plage linéaire et que vous ne déformiez pas ou ne détruisiez pas le haut-parleur. (L’amplificateur de 100 W produit deux fois plus de sones que le 10 W.)
Je me tiens à une distance R d’une petite source sonore (taille bien inférieure à R), au niveau du sol, en plein air, où les réflexions peuvent être négligées. Le niveau sonore est L. Si je me déplace maintenant à une distance nR (n un nombre, et nR toujours beaucoup plus grand que la taille de la source), quel sera le nouveau niveau sonore ?
Premièrement, notez que la négligence des réflexions est très importante. Ce calcul ne fonctionnera pas à l’intérieur d’une pièce, où les réflexions sur le mur (produisant collectivement la réverbération) rendent le calcul assez difficile. En plein air, l’intensité du son est proportionnelle à 1/r2, où r est la distance de la source. (La constante de proportionnalité dépend du degré de réflexion du sol et ne nous concerne pas ici, car elle s’annulera grossièrement dans le calcul, à condition que r soit raisonnablement grand). Ainsi, si on augmente r de R à nR, on diminue l’intensité de I à I/n 2.

La différence en décibels entre les deux signaux d’intensité I 2 et I 1 est définie ci-dessus comme étant
Par exemple, si n est égal à 2 (c’est-à-dire si on s’éloigne deux fois plus), l’intensité est réduite d’un facteur quatre et le niveau sonore passe de L à (L – 6dB).
Si, dans des conditions idéales de calme, un jeune peut entendre un son de 1 kHz à 0 dB émis par un haut-parleur (peut-être un softspeaker ?), de combien doit-on augmenter la puissance du haut-parleur pour porter le son à 110 dB (un niveau dangereusement fort mais auquel on peut survivre) ?
La différence en décibels entre les deux signaux de puissance P2 et P1 est définie ci-dessus comme étant
ce qui est une démonstration que l’oreille humaine possède une gamme dynamique remarquablement étendue, peut-être supérieure à celle de l’œil.
Un amplificateur a une entrée de 10 mV et une sortie de 2 V. Quel est son gain de tension en dB ?
La tension, comme la pression, apparaît au carré dans les expressions de puissance ou d’intensité. (La puissance dissipée dans une résistance R est V2/R.) Donc, par convention, on définit :
(Dans les cas acoustiques donnés ci-dessus, nous avons vu que le rapport de pression, exprimé en dB, était le même que le rapport de puissance : c’est la raison du facteur 20 lors de la définition du dB pour la pression. Il convient de noter que, dans l’exemple du gain en tension, il est peu probable que le gain en puissance de l’amplificateur soit égal au gain en tension, qui est défini par la convention utilisée ici. La puissance est proportionnelle au carré de la tension dans une résistance donnée. Cependant, les impédances d’entrée et de sortie des amplificateurs sont souvent très différentes. Par exemple, un amplificateur tampon ou émetteur-suiveur a un gain en tension d’environ 1, mais un gain en courant important).
Quelle est la différence, en dB, entre l’irradiance (intensité lumineuse) sur la terre (8,3 minutes-lumière du soleil) et sur Uranus (160 minutes-lumière) ?
Comme le son, l’intensité lumineuse isotrope diminue comme r-2, donc le rapport d’intensité est (160/8.3)2 = 20 log (160/8,3) = 26 dB.

Santé et sécurité au travail

Les différents pays et provinces ont évidemment des lois différentes concernant l’exposition au bruit au travail, qui sont appliquées avec un enthousiasme différent. Beaucoup de ces réglementations prévoient une limite d’exposition au bruit continu de 85 dB(A), pour un poste de travail de 8 heures. Pour chaque augmentation de 3 dB, l’exposition autorisée est réduite de moitié. Ainsi, si vous travaillez dans une boîte de nuit où la musique amplifiée produit 100 dB(A) près de vos oreilles, l’exposition autorisée est de 15 minutes. Il existe une limite pour les bruits d’impulsion comme les armes à feu ou les outils qui utilisent des explosifs. (Il existe de nombreux documents fournissant des conseils sur la manière de réduire l’exposition au bruit à la source (c’est-à-dire baisser le niveau de la musique), entre la source et l’oreille (c’est-à-dire s’éloigner des haut-parleurs lors d’un concert) et à l’oreille (c’est-à-dire porter des bouchons d’oreille ou des protections auditives industrielles). La gestion du bruit et la protection de l’ouïe au travail est le code de pratique de l’État de Nouvelle-Galles du Sud, en Australie (adresse de l’auteur).

Quelques questions fréquemment posées

Combien un avion est-il bruyant ? Un train ? Une personne qui chante ? Un chien qui aboie ? Un outil électrique ? Les réponses à cette question varient considérablement. Elles dépendent fortement de la distance à laquelle vous vous trouvez, du fait que vous soyez à l’intérieur ou non, de la présence ou non de réverbération, de la puissance de la source particulière et de son spectre. Donner des valeurs, sans être très précis sur les conditions, serait quelque peu trompeur. Parce que le reste de cette page est destiné à être fiable, dans la mesure où il va, je préfère ne pas donner de valeurs ici.
Comment « ajoute-t-on des décibels » ? », c’est-à-dire Quel niveau sonore obtient-on lorsqu’on ajoute le niveau a au niveau b ? Si les sources sont cohérentes (ce qui signifie généralement qu’elles proviennent finalement de la même source), alors il peut y avoir des effets d’interférence compliqués. Dans la plupart des cas, lorsque les sources sont indépendantes, on peut additionner les intensités et les convertir en décibels. Cependant, si l’on vous donne les niveaux sonores en dB(A), il n’est pas si facile de revenir à l’intensité, et il faut savoir quelque chose sur le spectre du son. Si vous connaissez la répartition du son dans différentes bandes de fréquences, vous pouvez utiliser l’applet sur ce lien.
Some of the questions on our FAQ in music acoustics relate to decibels, including
- Why do the sounds of two musical instruments always reinforce, and never cancel out?
- How much does one more violin add to the sound level of a section of n violins?
- Does adding two equal sounds give an increase of 3 or 6 dB? Why?
- What is the loudest sound?
- Is there really no sound in space?

Measure your own hearing response
Adding sound levels from incoherent sources
What are interference beats and Tartini tones?
FAQ in music acoustics
Loudness and spectra: how spectral content and other features are related to loudness
Formants: what are they? A discussion of the different meanings of this term
Music acoustics home page
Physclips: a multi-level, multimedia introduction to mechanics.
A list of other educational web sites from this author.