Distribution marginale

Distributions de probabilités > Distribution marginale

Qu’est-ce qu’une distribution marginale ?

Voyez la vidéo ou l’article ci-dessous :

La définition technique peut être un peu abrutissante à regarder:

Définition d’une distribution marginale = Si X et Y sont des variables aléatoires discrètes et f (x,y) est la valeur de
leur distribution de probabilité conjointe en (x,y), les fonctions données par :
g(x) = Σy f (x,y) et h(y) = Σx f (x,y) sont les distributions marginales de X et Y , respectivement.

Si vous êtes doué pour les équations, c’est probablement tout ce que vous devez savoir. Elle vous indique comment trouver une distribution marginale. Mais si cette formule vous donne mal à la tête (ce qui est le cas pour la plupart des gens !), vous pouvez utiliser un tableau de distribution de fréquences pour trouver une distribution marginale.

Une distribution marginale tire son nom du fait qu’elle apparaît dans les marges d’un tableau de distribution de probabilités.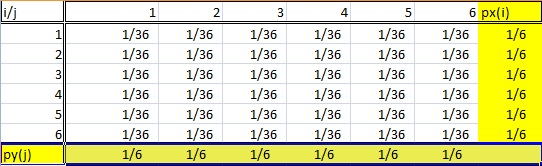

Bien sûr, ce n’est pas aussi simple que cela. Vous ne pouvez pas simplement regarder n’importe quel vieux tableau de distribution de fréquences et dire que la dernière colonne (ou ligne) est une « distribution marginale ». Les distributions marginales suivent quelques règles :

• La distribution doit provenir de données bivariées. Bivarié est juste une autre façon de dire  » deux variables « , comme X et Y. Dans le tableau ci-dessus, les variables aléatoires i et j proviennent du lancer de deux dés.
• Une distribution marginale est celle où vous ne vous intéressez qu’à l’une des variables aléatoires . En d’autres termes, soit X, soit Y. Si vous regardez le tableau de probabilité ci-dessus, les probabilités de somme d’une variable sont listées dans la ligne inférieure et les autres probabilités de somme sont listées dans la colonne de droite. Ce tableau a donc deux distributions marginales.

Différence entre la distribution marginale et la distribution conditionnelle.

Une distribution conditionnelle est celle où nous ne nous intéressons qu’à une sous-population particulière de notre ensemble de données. Dans l’exemple du lancer de dés, il pourrait s’agir de « lancer un deux » ou « lancer un six ». L’image ci-dessous montre deux sous-populations mises en évidence (et donc, deux distributions conditionnelles).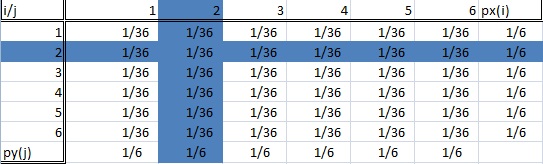

Comment calculer la probabilité de la distribution marginale

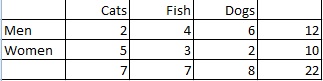
Exemple de question : Calculez la distribution marginale de la préférence pour les animaux de compagnie chez les hommes et les femmes :
Solution:
Étape 1 : comptez le nombre total de personnes. Dans ce cas, le total est donné dans la colonne de droite (22 personnes).
Étape 2 : Comptez le nombre de personnes qui préfèrent chaque type d’animal de compagnie, puis transformez le ratio en probabilité :
Personnes qui préfèrent les chats : 7/22 = 0,32
Personnes qui préfèrent les poissons : 7/22 = 0,32
Personnes qui préfèrent les chiens : 8/22 = 0,36
Conseil : Vous pouvez vérifier votre réponse en vous assurant que les probabilités sont toutes égales à 1.

Exemple question 2 (événements mutuellement exclusifs) : Si P(A) = 0,20, P(b) = 0,70, et que les deux événements s’excluent mutuellement, trouvez P(B’∩A), P(B’∩A’) et P(B∩A’).
Si vous n’êtes pas familier avec cette notation, P(A’) signifie  » pas A « , ou le complément. P(B’∩A) signifie  » l’intersection de pas B et A « ).

Réponse:
Vous pourriez calculer les probabilités individuellement, mais elles sont beaucoup plus faciles à calculer à l’aide d’un tableau.

Étape 1 : remplissez un tableau de fréquence avec les informations données. La probabilité totale doit être égale à 1, donc vous pouvez également l’ajouter aux marges (totaux). Une simple addition/algébre permet de remplir les blancs marginaux. Par exemple, sur la ligne du bas 0,70 + x = 1,00 donc Le total marginal pour B’ doit être de 0,30.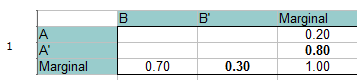

Étape 2 : Ajoutez 0 pour l’intersection de A et B, en haut à gauche du tableau. Vous pouvez le faire parce que A et B sont mutuellement exclusifs et ne peuvent pas se produire ensemble.

Étape 3 : Remplissez le reste des blancs en utilisant l’addition simple/l’algèbre.

Lecture du tableau (regardez les intersections des deux probabilités énoncées):
P(B’∩A) = 0,20
P(B’∩A’) = 0,10
P(B∩A’) = 0,70.

Exemple question 3 (événements indépendants) : Si P(A) = 0,20, P(b) = 0,70, et que les deux événements sont indépendants, trouvez P(B’∩A), P(B’∩A’) et P(B∩A’).

Réponse : Cette fois, A et B sont indépendants, donc la probabilité qu’ils se produisent tous les deux en même temps est de 0,14 (P(A)*P(B) = 0,20 * 0,70 = 0,14). Cette valeur est placée en haut à gauche (intersection de A et B). Remplissez le reste du tableau exactement de la même manière que dans les étapes précédentes.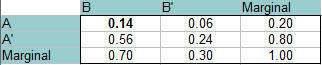

Lisez les réponses du tableau (à partir des intersections des deux probabilités):
P(B’∩A) : 0.06
P(B’∩A’) : 0,24
P(B∩A’) : 0,56.

Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL : CRC Press, pp. 536 et 571, 2002.
Agresti A. (1990) Analyse des données catégorielles. John Wiley and Sons, New York.
Everitt, B. S. ; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, deuxième édition (Schaum’s Easy Outlines) 2e édition. McGraw-Hill Education

——————————————————————————

Vous avez besoin d’aide pour un devoir ou une question de test ? Avec Chegg Study, vous pouvez obtenir des solutions étape par étape à vos questions de la part d’un expert en la matière. Vos 30 premières minutes avec un tuteur Chegg sont gratuites !