Interest Calculator
Our Interest Calculator can help determine the interest payments and final balances on not only fixed principal amounts, but also additional periodic contributions. There are also optional factors available for consideration such as tax on interest income and inflation. To understand and compare the different ways in which interest can be compounded, please visit our Compound Interest Calculator instead.

Results
Breakdown
|
.
Related Investment Calculator | Average Return Calculator | ROI Calculator
L’intérêt est la rémunération versée par l’emprunteur au prêteur pour l’utilisation de l’argent sous forme de pourcentage, ou un montant. Le concept d’intérêt est l’épine dorsale de la plupart des instruments financiers dans le monde. Bien que l’intérêt soit gagné, il est différent du profit en ce sens qu’il est reçu par un prêteur par opposition au propriétaire d’un actif ou d’un investissement, bien que l’intérêt puisse faire partie du profit sur un investissement.
Il existe deux méthodes distinctes d’accumulation de l’intérêt, catégorisées en intérêt simple ou en intérêt composé.
Intérêt simple
Voici un exemple de base du fonctionnement de l’intérêt. Derek aimerait emprunter 100 $ (généralement appelé le principal) à la banque pour un an. La banque veut un intérêt de 10 % sur ce montant. Pour calculer l’intérêt :
100 $ × 10 % = 10 $
Cet intérêt est ajouté au principal, et la somme devient le remboursement requis de Derek à la banque.
100 $ + 10 $ = 110 $
Derek doit 110 $ à la banque un an plus tard, 100 $ pour le principal et 10 $ d’intérêt.
Supposons que Derek voulait emprunter 100 $ pendant deux ans au lieu d’un, et que la banque calcule l’intérêt annuellement. Il lui serait simplement facturé le taux d’intérêt deux fois, une fois à la fin de chaque année.
100 $ + 10 $ (année 1) + 10 $ (année 2) = 120 $
Derek doit à la banque 120 $ deux ans plus tard, 100 $ pour le principal et 20 $ d’intérêts.
La formule pour calculer l’intérêt simple est la suivante :
intérêt = (principal) × (taux d’intérêt) × (durée)
Lorsqu’il s’agit de fréquences d’application de l’intérêt plus compliquées, par exemple mensuelles ou quotidiennes, utilisez la formule :
intérêt = (principal) × (taux d’intérêt) × (durée) / (fréquence)
Cependant, l’intérêt simple est très rarement utilisé dans le monde réel. Même lorsque les gens utilisent le mot courant » intérêt « , ils font généralement référence à un intérêt qui se compose.
Intérêt composé
L’intérêt composé nécessite plus d’une période, alors revenons à l’exemple de Derek empruntant 100 $ à la banque pendant deux ans à un taux d’intérêt de 10 %. Pour la première année, nous calculons les intérêts comme d’habitude.
100 $ × 10 % = 10 $
Ces intérêts sont ajoutés au principal, et la somme devient le remboursement requis de Derek à la banque pour cette période actuelle.
100 $ + 10 $ = 110 $
Cependant, l’année se termine, et vient une autre période. Pour les intérêts composés, plutôt que le montant initial, on utilise le principal + les intérêts accumulés depuis. Dans le cas de Derek :
110 $ × 10 % = 11 $
Les frais d’intérêt de Derek à la fin de l’année 2 sont de 11 $, qui s’ajoutent à ce qui est dû après l’année 1 :
110 $ + 11 $ = 121 $
Lorsque le prêt prend fin, la banque perçoit 121 $ de Derek au lieu de 120 $ s’il était calculé avec des intérêts simples à la place. Cela s’explique par le fait que les intérêts sont également gagnés sur les intérêts.
Plus les intérêts sont composés fréquemment au cours d’une période, plus les intérêts seront élevés sur un capital initial. Voici un graphique de Wikipedia qui montre justement cela, un investissement de 1 000 $ à différentes fréquences de composition rapportant 20 % d’intérêts.
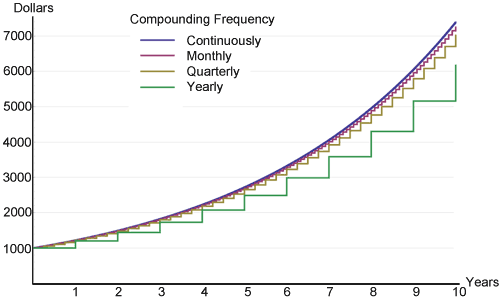
Il y a peu de différence au début entre toutes les fréquences, mais avec le temps, elles commencent lentement à diverger. C’est le pouvoir des intérêts composés dont tout le monde aime parler, illustré dans un graphique concis. Le composé continu aura toujours le rendement le plus élevé, en raison de son utilisation de la limite mathématique de la fréquence de composition qui peut se produire dans une période de temps donnée.
La règle de 72
Toute personne qui veut estimer les intérêts composés dans sa tête peut trouver la règle de 72 très utile. Non pas pour des calculs exacts comme ceux donnés par les calculatrices financières, mais pour avoir des idées de chiffres approximatifs. Elle stipule que pour trouver le nombre d’années (n) nécessaires pour doubler une certaine somme d’argent avec un taux d’intérêt quelconque, il suffit de diviser 72 par ce même taux.
Exemple : Combien de temps faudrait-il pour doubler 1 000 $ avec un taux d’intérêt de 8 % ?
n = 72/8 = 9
Il faudra 9 ans pour que les 1 000 $ deviennent 2 000 $ à un taux d’intérêt de 8 %. Cette formule fonctionne mieux pour les taux d’intérêt entre 6 et 10 %, mais elle devrait aussi fonctionner raisonnablement bien pour tout ce qui est inférieur à 20 %.
Taux d’intérêt fixe ou variable
Le taux d’intérêt d’un prêt ou d’une épargne peut être » fixe » ou » variable « . Les prêts ou l’épargne à taux variable sont normalement basés sur un certain taux de référence, comme le taux des fonds de la Réserve fédérale américaine (Fed) ou le LIBOR (London Interbank Offered Rate). Normalement, le taux de prêt est un peu plus élevé et le taux d’épargne un peu plus bas que le taux de référence. La différence va au profit de la banque. Le taux Fed et le LIBOR sont tous deux des taux d’intérêt interbancaires à court terme, mais le taux Fed est le principal outil utilisé par la Réserve fédérale pour influencer l’offre de monnaie dans l’économie américaine. Le LIBOR est un taux commercial calculé à partir des taux d’intérêt en vigueur entre des institutions très solvables. Notre calculateur d’intérêts traite uniquement des taux d’intérêt fixes.
Cotisations
Une distinction importante à faire concernant les cotisations est de savoir si elles interviennent au début ou à la fin des périodes de composition. Les paiements périodiques qui surviennent à la fin ont un total de période d’intérêt de moins par cotisation.
Taux d’imposition
Certaines formes de revenus d’intérêts sont soumises à l’impôt, notamment les obligations, l’épargne et les certificats de dépôts(CD). Aux États-Unis, les obligations de sociétés sont presque toujours imposées. Certains types sont entièrement imposés tandis que d’autres le sont partiellement ; par exemple, si les intérêts perçus sur les obligations du Trésor fédéral américain peuvent être imposés au niveau fédéral, ils sont exonérés au niveau des États et des collectivités locales. Les impôts peuvent avoir un impact très important sur le solde final. Par exemple, si Derek épargne 100 $ à 6 % pendant 20 ans, il obtiendra :
100 $ × (1 + 6 %)20 = 320,71
Ceci est exempt d’impôt. Cependant, si Derek a un taux d’imposition marginal de 25 %, il se retrouvera avec 239,78 $ uniquement parce que le taux d’imposition de 25 % s’applique à chaque période de capitalisation.
Taux d’inflation
L’inflation est définie comme une augmentation du niveau général des prix, où un montant fixe d’argent permettra relativement moins. Au cours des 100 dernières années, le taux d’inflation moyen aux États-Unis a oscillé autour de 3 %. À titre d’outil de comparaison, le taux de rendement annuel moyen de l’indice S&P 500 (Standard & Poor’s) aux États-Unis est d’environ 10 %. Veuillez consulter notre calculateur d’inflation pour des informations plus détaillées sur l’inflation.
Laissez le taux d’inflation à 0 pour des résultats rapides et généralisés. Mais pour des chiffres réels et précis, il est possible de saisir des chiffres afin de tenir compte de l’inflation.
L’impôt et l’inflation combinés rendent difficile la croissance de la valeur réelle de l’argent. Par exemple, aux États-Unis, la classe moyenne a un taux d’imposition marginal de 25 % et le taux d’inflation moyen est de 3 %. Pour maintenir la valeur de l’argent, il faut obtenir un taux d’intérêt ou un taux de rendement des investissements stable de 4 % ou plus, ce qui n’est pas facile à réaliser.