Kilogramme : Masse et Plancks Constante
Max Planck (1858-1947) n’avait à l’origine aucune idée de l’étendue de l’application de sa notion de « quantum », y compris de son rôle dans la mesure de la masse. Il l’a conçue dans le contexte d’un problème tenace de la physique du 19e siècle : Une théorie phare de l’époque prédisait de manière insensée que certains objets émettraient une puissance infinie lorsqu’ils libéraient un rayonnement électromagnétique à haute fréquence (et donc à courte longueur d’onde, c’est-à-dire vers la partie ultraviolette du spectre dans le graphique ci-dessous) – une situation qui devint connue sous le nom de « catastrophe ultraviolette ». »
Planck a postulé que l’énergie électromagnétique à une fréquence donnée ne pouvait être émise qu’en quantités discrètes, ou quanta, dont l’énergie est proportionnelle à h, maintenant connue comme la constante de Planck.
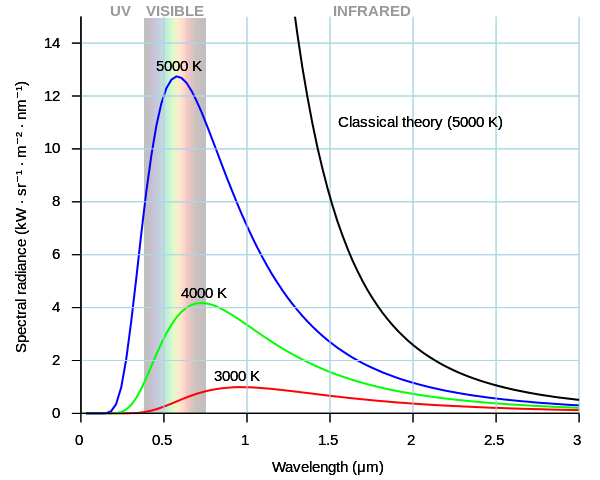
L’image ci-dessus montre ce que prédisait la théorie classique (la ligne noire) par rapport aux lignes bleue, verte et rouge dérivées de la formulation de Planck, qui sont en excellent accord avec les mesures physiques.
Masse, Planck et Einstein
Comment l’unité SI du kilogramme – incarnée dans un seul morceau de métal coulé au 19e siècle – pourrait-elle être redéfinie en termes d’un invariant de la nature et mise à l’échelle de manière pratique, précise et répétée ?

Après des décennies de débat, la communauté internationale des sciences de la mesure a choisi de répondre à cette question en utilisant la constante de Planck.
Pour de nombreux observateurs, le lien entre la masse à l’échelle d’un litre d’eau et une constante dérivant des tout premiers jours de la mécanique quantique peut ne pas être immédiatement évident. Le contexte scientifique de ce lien est suggéré par une relation sous-jacente profonde entre deux des formulations les plus célèbres de la physique.
L’une est la célèbre expression d’Einstein E =mc2, où E est l’énergie, m la masse et c la vitesse de la lumière. L’autre expression, moins connue du grand public mais fondamentale pour la science moderne, est E = hν, la première expression « quantique » de l’histoire, énoncée par Max Planck en 1900. Ici, E est l’énergie, ν est la fréquence (le ν n’est pas un « v » mais plutôt la lettre grecque minuscule nu), et h est ce que l’on appelle aujourd’hui la constante de Planck.
L’équation nist d’Einstein révèle que la masse peut être comprise et même quantifiée en termes d’énergie. La nist-équation de Planck montre que l’énergie, à son tour, peut être calculée en termes de fréquence ν d’une certaine entité telle qu’un photon (une particule de lumière), ou alternativement, avec quelques substitutions mathématiques, une masse – fois un multiple de h. Le multiple doit être un entier positif – comme 1, 2 ou 3. L’aspect entier est ce qui rend la relation « quantifiée » – la matière libère de l’énergie en morceaux discrets, connus sous le nom de « quanta », qui peuvent être imaginés comme des paquets individuels ou des paquets d’énergie.
La prise en compte des deux équations du nist donne un aperçu contre-intuitif mais extrêmement précieux : La masse – même à l’échelle des objets du quotidien – est intrinsèquement liée à h, que Planck a utilisé pour la première fois pour décrire le contenu énergétique extrêmement faible des photons individuels émis par les atomes des objets chauds. La valeur de h est d’environ 0,6 trillionième d’un trillionième d’un milliardième d’un joule-seconde. Le joule est l’unité SI de l’énergie.
Dans la pratique, les expériences reliant la masse à h avec une précision extraordinaire sont devenues possibles à la fin du XXe siècle à la suite de deux découvertes distinctes qui ont conduit à deux constantes physiques différentes liées respectivement à la tension et à la résistance.
Ce sont la constante de Josephson (KJ = 2e/h) et la constante de von Klitzing (RK = h/e2).
La constante de Josephson est liée à l’effet Josephson en courant alternatif. Celui-ci se produit lorsqu’une tension appliquée aux bornes d’une jonction supraconductrice crée un courant électrique alternatif dont la fréquence est proportionnelle à la tension. La fréquence peut être mesurée plus précisément que toute autre quantité (ce qui est régulièrement exploité par les horloges atomiques, qui se verrouillent sur les fréquences micro-ondes ou optiques du rayonnement électromagnétique émis par les atomes). Le KJ constitue un moyen extrêmement précis de mesurer la tension.
La constante de von Klitzing RK décrit la façon dont la résistance électrique existe en valeurs discrètes et quantifiées (au lieu de valeurs continues) dans certains types de systèmes physiques. En raison de sa précision extraordinairement élevée, la RK est employée dans le monde entier comme norme de résistance électrique.
Balances ou sphères ?
Dans les années 1990, le débat s’intensifiait sur les moyens possibles de redéfinir le kilogramme qui permettraient d’éliminer l’étalon artefact. Deux principales écoles de pensée ont émergé. L’une définirait le kilogramme en fonction de la masse d’un atome de silicium en comptant le nombre d’atomes dans une sphère de 1 kg de silicium-28 ultra-pur (l’isotope le plus abondant du silicium, qui contient un total de 28 protons et neutrons).
L’autre a été défendue, entre autres, par les scientifiques du NIST Peter Mohr et Barry Taylor. En 1999, dans une lettre publiée dans la revue Metrologia, ils ont proposé d’attribuer une valeur fixe à la constante de Planck comme base d’une nouvelle définition du kilogramme. Mohr et Taylor ont exploré l’utilisation d’une balance Kibble, un appareil complexe qui mesure la masse avec précision grâce à des mesures électriques.
Nommée d’après le physicien britannique Bryan Kibble, la balance Kibble a été développée pour la première fois en 1975 au National Physical Laboratory (NPL) du Royaume-Uni. Une autre a été construite peu après au NIST. Dans les années 1980, les scientifiques du NPL et du NIST étaient fortement impliqués dans l’utilisation des balances Kibble pour déterminer la valeur de h.
Mohr et Taylor ont raisonné que si une balance Kibble pouvait utiliser une masse exactement définie pour mesurer la valeur inconnue de h, alors le processus pouvait être inversé : en fixant une valeur fixe exacte de h, le même système pouvait être utilisé pour mesurer une masse inconnue.
L’idée, qui a été connue sous le nom de kilogramme « électrique » ou « électronique », a été largement discutée et finalement approuvée en principe par la Conférence générale internationale des poids et mesures (CGPM), avec quelques exigences. Trois expériences au moins doivent produire des mesures dont l’incertitude-type relative ne dépasse pas 50 parties par milliard, l’une de ces mesures au moins ayant une incertitude ne dépassant pas 20 parties par milliard. Toutes ces valeurs doivent concorder avec un niveau de confiance statistique de 95 %.
A la mi-2017, la communauté scientifique internationale a relevé le défi et a réussi à répondre à ces exigences.

Plus d’une demi-douzaine de balances Kibble sont en service dans le monde. La mesure h finale du NIST soumise pour la redéfinition du SI avait une incertitude de 13 parties par milliard. Une autre mesure de la balance Kibble, provenant du Conseil national de recherches du Canada (CNRC), avait une incertitude de seulement 9,1 parties par milliard. (Le CNRC avait reçu une balance Kibble du NPL en 2009.) Deux autres mesures de la balance Kibble, dont une du LNE (Laboratoire National de Métrologie et d’Essais en France), présentaient les niveaux d’exactitude requis. Quatre mesures de la « sphère de silicium » d’Avogadro ont également satisfait aux exigences internationales, dont trois de la multinationale IAC (International Avogadro Coordination) et une du NMIJ (National Metrology Institute of Japan).
Lorsqu’elles ont été analysées par le CODATA Task Group on Fundamental Constants, les mesures ont donné une valeur finale de h de 6,62607015 × 10-34 kg⋅m2/s, avec une incertitude de 10 parties par milliard. Lors de la redéfinition du SI, cette valeur a été fixée comme la valeur exacte de la constante de Planck, qui définit à son tour d’autres unités du SI, dont le kilogramme.
.