Probabilité théorique versus probabilité expérimentale
Vous avez entendu les termes, probabilité théorique et probabilité expérimentale, mais que signifient-ils ?
Est-ce qu’elles sont liées de quelque manière que ce soit ? C’est ce que nous allons découvrir dans cette leçon.
Si vous avez suivi les leçons sur la probabilité indépendante et dépendante, alors vous avez déjà trouvé la probabilité théorique pour de nombreux problèmes.
Probabilité théorique
La probabilité théorique est la probabilité qui est calculée à l’aide de formules mathématiques. C’est la probabilité basée sur la théorie mathématique.
Probabilité expérimentale
La probabilité expérimentale est calculée lorsque la situation ou le problème réel est réalisé comme une expérience. Dans ce cas, vous réaliseriez l’expérience et utiliseriez les résultats réels pour déterminer la probabilité.
Pour réaliser avec précision une expérience, vous devez :
- Identifier ce qui constitue un » essai « .
- Réaliser un minimum de 25 essais
- Mettre en place un organisateur (tableau ou graphique) pour enregistrer vos données.
Regardons un exemple où nous calculons d’abord la probabilité théorique, puis réalisons l’expérience pour déterminer la probabilité expérimentale.
Il sera intéressant de comparer la probabilité théorique et la probabilité expérimentale. Pensez-vous que les deux calculs seront proches ?
Exemple 1 – Théorique versus expérimental
Ce problème est tiré de l’exemple 1 de la leçon sur les événements indépendants. Nous avons calculé que la probabilité théorique était de 1/12 ou 8,3 %. Jetez un coup d’œil:
Probabilité théorique

Puisque nous savons que la probabilité théorique est de 8,3 % de chances de tirer à pile ou face et de rouler un 6, voyons ce qui se passe lorsque nous réalisons réellement l’expérience.
Probabilité expérimentale
Identifiez un essai : Un essai consiste à tirer à pile ou face une fois et à lancer un dé une fois.
Réaliser 25 essais et enregistrer vos données dans le tableau ci-dessous.
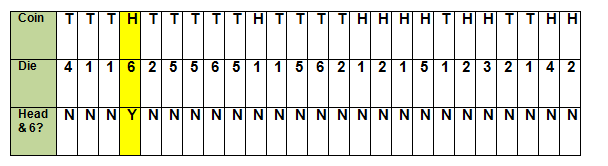
Pour chaque essai, j’ai tiré à pile ou face une fois et lancé le dé. J’ai enregistré un H pour pile et un T pour face dans la ligne intitulée » Pièce de monnaie « .
J’ai enregistré le nombre sur le dé dans la ligne intitulée » Dé « .
Dans la dernière ligne, j’ai déterminé si l’essai a réalisé l’événement consistant à tirer à pile et à lancer un six.
Dans cette expérience, il n’y a eu qu’un seul essai (sur 25) où une tête a été retournée sur la pièce de monnaie et un 6 a été obtenu sur le dé.
Cela signifie que la probabilité expérimentale est de 1/25 ou 4%.
Tip
Veuillez noter que l’expérience de chacun sera différente ; ce qui permet à la probabilité expérimentale de différer.
Aussi, plus vous effectuerez d’essais dans votre expérience, plus vos calculs seront proches pour les probabilités expérimentales et théoriques.
Conclusions
La probabilité théorique est de 8,3 % et la probabilité expérimentale est de 4 %. Bien que la probabilité expérimentale soit légèrement inférieure, il ne s’agit pas d’une différence significative.
Dans la plupart des expériences, la probabilité théorique et la probabilité expérimentale ne seront pas égales ; cependant, elles devraient être relativement proches.
If the calculations are not close, then there’s a possibility that the experiment was conducted improperly or more trials need to be completed.
I hope this helps to give you a sense of how to set up an experiment in order to compare theoretical versus experimental probabilities.
- Home
- Probability
- Theoretical/Experimental Probability
>
>

Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.