Qu’est-ce que l’astuce du noyau ? Pourquoi est-il important ?
Lorsque l’on parle de noyaux en apprentissage automatique, il est fort probable que la première chose qui vous vienne à l’esprit soit le modèle des machines à vecteurs de support (SVM) car l’astuce du noyau est largement utilisée dans le modèle SVM pour faire le pont entre linéarité et non-linéarité.
Pour vous aider à comprendre ce qu’est un noyau et pourquoi il est important, je vais d’abord présenter les bases du modèle SVM.
Le modèle SVM est un modèle d’apprentissage automatique supervisé qui est principalement utilisé pour les classifications (mais il pourrait aussi être utilisé pour la régression !). Il apprend à séparer différents groupes en formant des frontières de décision.

Dans le graphique ci-dessus, on remarque qu’il y a deux classes d’observations : les points bleus et les points violets. Il existe des tonnes de façons de séparer ces deux classes, comme le montre le graphique de gauche. Cependant, nous voulons trouver le « meilleur » hyperplan qui pourrait maximiser la marge entre ces deux classes, ce qui signifie que la distance entre l’hyperplan et les points de données les plus proches de chaque côté est la plus grande. Selon le côté de l’hyperplan où se situe un nouveau point de données, nous pourrions attribuer une classe à la nouvelle observation.
Cela semble simple dans l’exemple ci-dessus. Cependant, toutes les données ne sont pas linéairement séparables. En fait, dans le monde réel, presque toutes les données sont distribuées de manière aléatoire, ce qui rend difficile la séparation linéaire de différentes classes.

Pourquoi est-il important d’utiliser l’astuce du noyau ?
Comme vous pouvez le voir dans l’image ci-dessus, si nous trouvons un moyen de mapper les données d’un espace bidimensionnel à un espace tridimensionnel, nous pourrons trouver une surface de décision qui divise clairement entre différentes classes. Ma première pensée de ce processus de transformation des données est de mapper tous les points de données à une dimension supérieure (dans ce cas, 3 dimensions), de trouver la frontière et de faire la classification.
Cela semble correct. Cependant, lorsqu’il y a de plus en plus de dimensions, les calculs dans cet espace deviennent de plus en plus coûteux. C’est là qu’intervient l’astuce du noyau. Elle nous permet d’opérer dans l’espace caractéristique original sans calculer les coordonnées des données dans un espace de dimension supérieure.
Regardons un exemple :
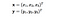
Ici, x et y sont deux points de données en 3 dimensions. Supposons que nous devions transposer x et y dans un espace à 9 dimensions. Nous devons effectuer les calculs suivants pour obtenir le résultat final, qui n’est qu’un scalaire. La complexité de calcul, dans ce cas, est O(n²).

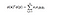
However, if we use the kernel function, which is denoted as k(x, y), instead of doing the complicated computations in the 9-dimensional space, we reach the same result within the 3-dimensional space by calculating the dot product of x -transpose and y. The computational complexity, in this case, is O(n).
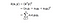
In essence, what the kernel trick does for us is to offer a more efficient and less expensive way to transform data into higher dimensions. With that saying, the application of the kernel trick is not limited to the SVM algorithm. Tout calcul impliquant les produits scalaires (x, y) peut utiliser l’astuce du noyau.
Différentes fonctions de noyau
Il existe différents noyaux. Les plus populaires sont le noyau polynomial et le noyau à fonction de base radiale (RBF).
« Intuitivement, le noyau polynomial examine non seulement les caractéristiques données des échantillons d’entrée pour déterminer leur similarité, mais aussi les combinaisons de celles-ci » (Wikipedia), tout comme l’exemple ci-dessus. Avec n caractéristiques originales et d degrés de polynôme, le noyau polynomial donne n^d caractéristiques étendues.
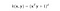
.
Le noyau RBF est aussi appelé noyau gaussien. Il y a un nombre infini de dimensions dans l’espace caractéristique car il peut être étendu par la série de Taylor. Dans le format ci-dessous, le paramètre γ définit l’influence d’un seul exemple de formation. Plus il est grand, plus les autres exemples doivent être proches pour être affectés (documentation sklearn).
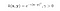
Il existe différentes options pour les fonctions du noyau dans la bibliothèque sklearn en Python. Vous pouvez même construire un noyau personnalisé si nécessaire.
La fin
L’astuce du noyau semble être un plan » parfait « . Cependant, une chose critique à garder à l’esprit est que lorsque nous mappons des données à une dimension supérieure, il y a des chances que nous puissions surajuster le modèle. Ainsi, choisir la bonne fonction noyau (y compris les bons paramètres) et la régularisation sont d’une grande importance.
Si vous êtes curieux de savoir ce qu’est la régularisation, j’ai écrit un article parlant de ma compréhension de celle-ci et vous pouvez le trouver ici.
J’espère que vous apprécierez cet article. Comme toujours, n’hésitez pas à me faire savoir si vous avez des questions, des commentaires, des suggestions, etc. Merci de votre lecture 🙂