Qu’est-ce qu’un filtre passe-bas ? Un tutoriel sur les bases des filtres RC passifs

décembre 5, 2021admin

Qu’est-ce que le filtrage ? Apprenez ce que sont les filtres passe-bas à résistance-capacité (RC) et où vous pouvez les utiliser.

Cet article présente le concept de filtrage et explique en détail le but et les caractéristiques des filtres passe-bas à résistance-capacité (RC).

Domaine temporel et domaine fréquentiel

Lorsque vous regardez un signal électrique sur un oscilloscope, vous voyez une ligne qui représente les changements de tension par rapport au temps. À tout moment spécifique dans le temps, le signal n’a qu’une seule valeur de tension. Ce que vous voyez sur l’oscilloscope est la représentation du signal dans le domaine temporel.

Une trace d’oscilloscope typique est simple et intuitive, mais elle est aussi quelque peu restrictive, car elle ne révèle pas directement le contenu fréquentiel d’un signal. Contrairement à la représentation dans le domaine temporel, dans laquelle un instant correspond à une seule valeur de tension, une représentation dans le domaine fréquentiel (également appelée spectre) transmet des informations sur un signal en identifiant les différentes composantes de fréquence présentes simultanément.

Représentations dans le domaine temporel d’une sinusoïde (en haut) et d’une onde carrée (en bas).

Représentations dans le domaine fréquentiel d’une sinusoïde (en haut) et d’une onde carrée (en bas).

Qu’est-ce qu’un filtre ?

Un filtre est un circuit qui élimine, ou » filtre « , une plage spécifiée de composantes de fréquence. En d’autres termes, il sépare le spectre du signal en composantes de fréquence qui seront transmises et en composantes de fréquence qui seront bloquées.

Si vous n’avez pas beaucoup d’expérience de l’analyse dans le domaine fréquentiel, vous pouvez encore avoir des doutes sur ce que sont ces composantes de fréquence et comment elles coexistent dans un signal qui ne peut pas avoir plusieurs valeurs de tension en même temps. Voyons un bref exemple qui aidera à clarifier ce concept.

Imaginons que nous avons un signal audio qui consiste en une onde sinusoïdale parfaite de 5 kHz. Nous savons à quoi ressemble une onde sinusoïdale dans le domaine temporel, et dans le domaine fréquentiel, nous ne verrons rien d’autre qu’un « pic » de fréquence à 5 kHz. Supposons maintenant que nous activions un oscillateur de 500 kHz qui introduit un bruit haute fréquence dans le signal audio.

Le signal tel qu’il est vu sur un oscilloscope ne sera toujours qu’une seule séquence de tensions, avec une valeur par instant, mais le signal aura un aspect différent car ses variations dans le domaine temporel doivent maintenant refléter à la fois l’onde sinusoïdale de 5 kHz et les fluctuations du bruit haute fréquence.

Dans le domaine fréquentiel, cependant, l’onde sinusoïdale et le bruit sont des composantes fréquentielles distinctes qui sont présentes simultanément dans ce seul signal. L’onde sinusoïdale et le bruit occupent différentes portions de la représentation du signal dans le domaine fréquentiel (comme le montre le schéma ci-dessous), ce qui signifie que nous pouvons filtrer le bruit en dirigeant le signal à travers un circuit qui laisse passer les basses fréquences et bloque les hautes fréquences.

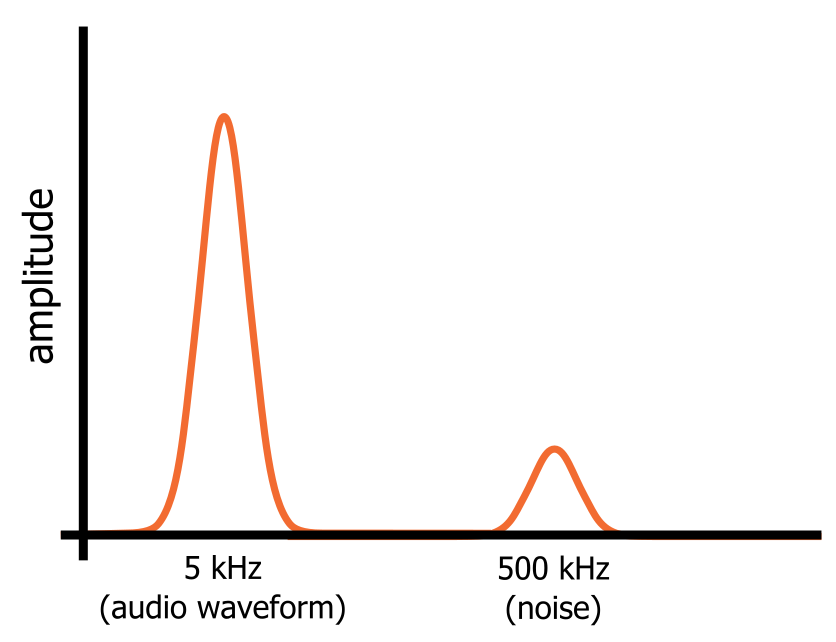
Types de filtres

Les filtres peuvent être placés dans de grandes catégories qui correspondent aux caractéristiques générales de la réponse en fréquence du filtre. Si un filtre laisse passer les basses fréquences et bloque les hautes fréquences, on l’appelle un filtre passe-bas. S’il bloque les basses fréquences et laisse passer les hautes fréquences, il s’agit d’un filtre passe-haut. Il existe également des filtres passe-bande, qui ne laissent passer qu’une gamme relativement étroite de fréquences, et des filtres coupe-bande, qui ne bloquent qu’une gamme relativement étroite de fréquences.

Les filtres peuvent également être classés en fonction des types de composants utilisés pour mettre en œuvre le circuit. Les filtres passifs utilisent des résistances, des condensateurs et des inductances ; ces composants n’ont pas la capacité de fournir une amplification, et par conséquent un filtre passif ne peut que maintenir ou réduire l’amplitude d’un signal d’entrée. Un filtre actif, en revanche, peut à la fois filtrer un signal et appliquer un gain, car il comprend un composant actif tel qu’un transistor ou un amplificateur opérationnel.

Ce filtre passe-bas actif est basé sur la topologie populaire de Sallen-Key.

Cet article explore l’analyse et la conception des filtres passe-bas passifs. Ces circuits jouent un rôle important dans une grande variété de systèmes et d’applications.

Le filtre passe-bas RC

Pour créer un filtre passe-bas passif, nous devons combiner un élément résistif avec un élément réactif. En d’autres termes, nous avons besoin d’un circuit composé d’une résistance et soit d’un condensateur, soit d’une inductance. En théorie, la topologie passe-bas résistance-inductance (RL) est équivalente, en termes de capacité de filtrage, à la topologie passe-bas résistance-capacité (RC). En pratique, cependant, la version résistance-capacité est beaucoup plus courante, et par conséquent, le reste de cet article se concentrera sur le filtre passe-bas RC.

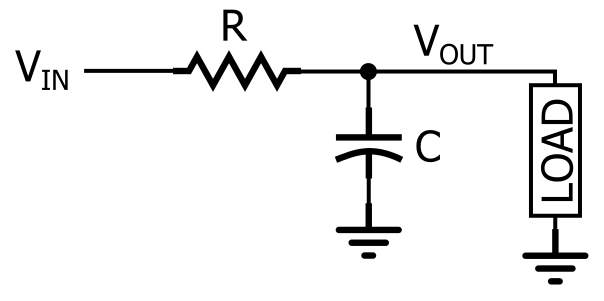
Le filtre passe-bas RC.

Comme vous pouvez le voir sur le schéma, une réponse passe-bas RC est créée en plaçant une résistance en série avec le chemin du signal et un condensateur en parallèle avec la charge. Dans le schéma, la charge est un composant unique, mais dans un circuit réel, il pourrait s’agir de quelque chose de beaucoup plus compliqué, comme un convertisseur analogique-numérique, un amplificateur ou l’étage d’entrée de l’oscilloscope que vous utilisez pour mesurer la réponse du filtre.

Nous pouvons analyser intuitivement l’action de filtrage de la topologie RC passe-bas si nous reconnaissons que la résistance et le condensateur forment un diviseur de tension dépendant de la fréquence.

Le filtre passe-bas RC redessiné pour qu’il ressemble à un diviseur de tension.

Lorsque la fréquence du signal d’entrée est basse, l’impédance du condensateur est élevée par rapport à l’impédance de la résistance ; ainsi, la majeure partie de la tension d’entrée chute aux bornes du condensateur (et de la charge, qui est en parallèle avec le condensateur). Lorsque la fréquence d’entrée est élevée, l’impédance du condensateur est faible par rapport à l’impédance de la résistance, ce qui signifie qu’une plus grande partie de la tension d’entrée chute aux bornes de la résistance et qu’une moindre quantité est transférée à la charge. Ainsi, les basses fréquences passent et les hautes fréquences sont bloquées.

Cette explication qualitative de la fonctionnalité passe-bas RC est une première étape importante, mais elle n’est pas très utile lorsque nous devons réellement concevoir un circuit, car les termes « haute fréquence » et « basse fréquence » sont extrêmement vagues. Les ingénieurs doivent créer des circuits qui laissent passer et bloquent des fréquences spécifiques. Par exemple, dans le système audio décrit ci-dessus, nous voulons préserver un signal de 5 kHz et supprimer un signal de 500 kHz. Cela signifie que nous avons besoin d’un filtre qui passe du passage au blocage quelque part entre 5 kHz et 500 kHz.

La fréquence de coupure

La gamme de fréquences pour laquelle un filtre ne provoque pas d’atténuation significative est appelée bande passante, et la gamme de fréquences pour laquelle le filtre provoque une atténuation significative est appelée bande d’arrêt. Les filtres analogiques, tels que le filtre passe-bas RC, passent toujours progressivement de la bande passante à la bande d’arrêt. Cela signifie qu’il est impossible d’identifier une fréquence à laquelle le filtre cesse de laisser passer les signaux et commence à les bloquer. Cependant, les ingénieurs ont besoin d’un moyen de résumer de manière pratique et concise la réponse en fréquence d’un filtre, et c’est là que le concept de fréquence de coupure entre en jeu.

Lorsque vous regardez un tracé de la réponse en fréquence d’un filtre RC, vous remarquerez que le terme « fréquence de coupure » n’est pas très précis. L’image du spectre d’un signal « coupé » en deux moitiés, dont l’une est conservée et l’autre écartée, ne s’applique pas, car l’atténuation augmente progressivement à mesure que les fréquences passent de sous la coupure à au-dessus de la coupure.

La fréquence de coupure d’un filtre RC passe-bas est en fait la fréquence à laquelle l’amplitude du signal d’entrée est réduite de 3 dB (cette valeur a été choisie parce qu’une réduction de 3 dB de l’amplitude correspond à une réduction de 50 % de la puissance). Ainsi, la fréquence de coupure est également appelée fréquence de -3 dB, et cette appellation est en fait plus précise et plus informative. Le terme bande passante fait référence à la largeur de la bande passante d’un filtre, et dans le cas d’un filtre passe-bas, la bande passante est égale à la fréquence de -3 dB (comme le montre le schéma ci-dessous).

Ce schéma traduit les caractéristiques génériques de la réponse en fréquence d’un filtre passe-bas RC. La bande passante est égale à la fréquence de -3 dB.

Comme expliqué ci-dessus, le comportement passe-bas d’un filtre RC est causé par l’interaction entre l’impédance indépendante de la fréquence de la résistance et l’impédance dépendante de la fréquence du condensateur. Pour déterminer les détails de la réponse en fréquence d’un filtre, nous devons analyser mathématiquement la relation entre la résistance (R) et la capacité (C), et nous pouvons également manipuler ces valeurs afin de concevoir un filtre répondant à des spécifications précises. La fréquence de coupure (fC) d’un filtre passe-bas RC se calcule comme suit :

Regardons un exemple de conception simple. Les valeurs des condensateurs sont plus restrictives que celles des résistances, nous commencerons donc par une valeur courante de capacité (comme 10 nF), puis nous utiliserons l’équation pour déterminer la valeur de résistance requise. L’objectif est de concevoir un filtre qui préservera une forme d’onde audio de 5 kHz et rejettera une forme d’onde de bruit de 500 kHz. Nous essaierons une fréquence de coupure de 100 kHz, et plus tard dans l’article, nous analyserons plus attentivement l’effet de ce filtre sur les deux composantes de fréquence.

Donc, une résistance de 160 Ω associée à un condensateur de 10 nF nous donnera un filtre qui se rapproche étroitement de la réponse en fréquence souhaitée.

Calcul de la réponse du filtre

Nous pouvons calculer le comportement théorique d’un filtre passe-bas en utilisant une version dépendant de la fréquence d’un calcul typique de diviseur de tension. La sortie d’un diviseur de tension résistif s’exprime comme suit :

Le filtre RC utilise une structure équivalente, mais au lieu de R2, nous avons un condensateur. Tout d’abord, nous remplaçons R2 (au numérateur) par la réactance du condensateur (XC). Ensuite, nous devons calculer la magnitude de l’impédance totale et la placer au dénominateur. Ainsi, nous avons

La réactance d’un condensateur indique la quantité d’opposition au passage du courant, mais contrairement à la résistance, la quantité d’opposition dépend de la fréquence du signal qui traverse le condensateur. Ainsi, nous devons calculer la réactance à une fréquence spécifique, et l’équation que nous utilisons pour cela est la suivante :

Dans l’exemple de conception ci-dessus, R ≈ 160 Ω et C = 10 nF. Nous supposerons que l’amplitude de VIN est de 1 V, de sorte que nous pouvons simplement retirer VIN du calcul. Calculons d’abord l’amplitude de VOUT à la fréquence de l’onde sinusoïdale :

L’amplitude de l’onde sinusoïdale est essentiellement inchangée. C’est bien, puisque notre intention était de préserver l’onde sinusoïdale tout en supprimant le bruit. Ce résultat n’est pas surprenant, puisque nous avons choisi une fréquence de coupure (100 kHz) qui est beaucoup plus élevée que la fréquence de l’onde sinusoïdale (5 kHz).

Voyons maintenant avec quel succès le filtre atténuera la composante bruit.

L’amplitude du bruit n’est plus que d’environ 20 % de sa valeur initiale.

Visualisation de la réponse du filtre

Le moyen le plus pratique d’évaluer l’effet d’un filtre sur un signal est d’examiner un graphique de la réponse en fréquence du filtre. Ces graphiques, souvent appelés tracés de Bode, ont l’amplitude (en décibels) sur l’axe vertical et la fréquence sur l’axe horizontal ; l’axe horizontal a généralement une échelle logarithmique, de sorte que la distance physique entre 1 Hz et 10 Hz est la même que la distance physique entre 10 Hz et 100 Hz, entre 100 Hz et 1 kHz, et ainsi de suite. Cette configuration nous permet d’évaluer rapidement et précisément le comportement d’un filtre sur une très large gamme de fréquences.

Un exemple de tracé de réponse en fréquence.

Chaque point de la courbe indique l’amplitude qu’aura le signal de sortie si le signal d’entrée a une amplitude de 1 V et une fréquence égale à la valeur correspondante sur l’axe horizontal. Par exemple, lorsque la fréquence d’entrée est de 1 MHz, l’amplitude de sortie (en supposant une amplitude d’entrée de 1 V) sera de 0,1 V (car -20 dB correspond à une réduction d’un facteur dix).

La forme générale de cette courbe de réponse en fréquence deviendra très familière à mesure que vous passerez plus de temps avec les circuits de filtrage. La courbe est presque parfaitement plate dans la bande passante, puis elle commence à baisser plus rapidement lorsque la fréquence d’entrée se rapproche de la fréquence de coupure. Finalement, le taux de variation de l’atténuation, appelé roll-off, se stabilise à 20 dB/décade – c’est-à-dire que l’amplitude du signal de sortie est réduite de 20 dB pour chaque augmentation d’un facteur dix de la fréquence d’entrée.

Évaluer les performances du filtre passe-bas

Si nous traçons soigneusement la réponse en fréquence du filtre que nous avons conçu plus tôt dans l’article, nous verrons que la réponse en amplitude à 5 kHz est essentiellement de 0 dB (c’est-à-dire, atténuation presque nulle) et que la réponse en amplitude à 500 kHz est d’environ -14 dB (ce qui correspond à un gain de 0,2). Ces valeurs sont cohérentes avec les résultats des calculs que nous avons effectués dans la section précédente.

Parce que les filtres RC ont toujours une transition graduelle de la bande passante à la bande d’arrêt, et parce que l’atténuation n’atteint jamais l’infini, nous ne pouvons pas concevoir un filtre » parfait « , c’est-à-dire un filtre qui n’a aucun effet sur l’onde sinusoïdale et qui élimine complètement le bruit. Au lieu de cela, nous devons toujours faire un compromis. Si nous rapprochons la fréquence de coupure de 5 kHz, nous aurons plus d’atténuation du bruit mais aussi plus d’atténuation de l’onde sinusoïdale que nous voulons envoyer à un haut-parleur. Si nous rapprochons la fréquence de coupure de 500 kHz, nous aurons moins d’atténuation à la fréquence de l’onde sinusoïdale, mais aussi moins d’atténuation à la fréquence du bruit.

Déphasage du filtre passe-bas

Jusqu’à présent, nous avons abordé la manière dont un filtre modifie l’amplitude des différentes composantes de fréquence d’un signal. Cependant, les éléments de circuit réactifs introduisent toujours un déphasage en plus des effets d’amplitude.

Le concept de phase fait référence à la valeur d’un signal périodique à un moment spécifique dans un cycle. Ainsi, lorsque nous disons qu’un circuit provoque un déphasage, nous voulons dire qu’il crée un désalignement entre le signal d’entrée et le signal de sortie : les signaux d’entrée et de sortie ne commencent et ne terminent plus leurs cycles au même moment dans le temps. La valeur du déphasage, par exemple 45° ou 90°, indique l’ampleur du désalignement créé.

Chaque élément réactif d’un circuit introduit 90° de déphasage, mais ce déphasage ne se produit pas en une seule fois. La phase du signal de sortie, tout comme l’amplitude du signal de sortie, change progressivement à mesure que la fréquence d’entrée augmente. Dans un filtre passe-bas RC, nous avons un élément réactif (le condensateur), et par conséquent le circuit finira par introduire 90° de déphasage.

Comme pour la réponse en magnitude, la réponse en phase est plus facilement évaluée en examinant un graphique dans lequel l’axe horizontal indique la fréquence logarithmique. La description ci-dessous transmet le schéma général, puis vous pouvez compléter les détails en examinant le tracé.

Le déphasage est initialement de 0°.
Il augmente progressivement jusqu’à atteindre 45° à la fréquence de coupure ; pendant cette partie de la réponse, le taux de variation est croissant.
Après la fréquence de coupure, le déphasage continue d’augmenter, mais le taux de changement diminue.
Le taux de changement devient très faible lorsque le déphasage s’approche asymptotiquement de 90°.

La ligne continue est la réponse en magnitude, et la ligne pointillée est la réponse en phase. La fréquence de coupure est de 100 kHz. Notez que le déphasage est de 45° à la fréquence de coupure.

Filtres passe-bas de deuxième ordre

Jusqu’à présent, nous avons supposé qu’un filtre passe-bas RC se compose d’une résistance et d’un condensateur. Cette configuration est un filtre de premier ordre.

L' » ordre » d’un filtre passif est déterminé par le nombre d’éléments réactifs – c’est-à-dire les condensateurs ou les inductances – présents dans le circuit. Un filtre d’ordre supérieur comporte plus d’éléments réactifs, ce qui entraîne un déphasage plus important et un amortissement plus abrupt. Cette deuxième caractéristique est la principale motivation pour augmenter l’ordre d’un filtre.

En ajoutant un élément réactif à un filtre – par exemple, en passant du premier ordre au deuxième ordre ou du deuxième ordre au troisième ordre – nous augmentons le roll-off maximal de 20 dB/décade. Un roll-off plus marqué se traduit par une transition plus rapide d’une faible atténuation à une forte atténuation, ce qui peut se traduire par une amélioration des performances lorsque le signal ne présente pas une large bande de fréquences qui sépare les composantes de fréquence souhaitées des composantes de bruit.

Les filtres du deuxième ordre sont généralement construits autour d’un circuit résonnant constitué d’une inductance et d’un condensateur (cette topologie est appelée « RLC » pour resistor-inductor-capacitor). Cependant, il est également possible de créer des filtres RC du second ordre. Comme le montre le schéma ci-dessous, il suffit de mettre en cascade deux filtres RC de premier ordre.

Bien que cette topologie crée certainement une réponse de second ordre, elle n’est pas très utilisée – comme nous le verrons dans la section suivante, la réponse en fréquence est souvent inférieure à celle d’un filtre actif de second ordre ou d’un filtre RLC de second ordre.

Réponse en fréquence du filtre RC du second ordre

On peut tenter de créer un filtre passe-bas RC du second ordre en concevant un filtre du premier ordre en fonction de la fréquence de coupure souhaitée, puis en connectant deux de ces étages du premier ordre en série. Cela permet effectivement d’obtenir un filtre dont la réponse en fréquence globale est similaire et dont le roll-off maximal est de 40 dB/décade au lieu de 20 dB/décade.

Toutefois, si nous examinons la réponse de plus près, nous constatons que la fréquence à -3 dB a diminué. Le filtre RC du second ordre ne se comporte pas comme prévu parce que les deux étages ne sont pas indépendants – nous ne pouvons pas simplement connecter ces deux étages ensemble et analyser le circuit comme un filtre passe-bas du premier ordre suivi d’un filtre passe-bas du premier ordre identique.

De plus, même si nous insérons un tampon entre les deux étages, de sorte que le premier étage RC et le second étage RC puissent fonctionner comme des filtres indépendants, l’atténuation à la fréquence de coupure originale sera de 6 dB au lieu de 3 dB. Cela se produit précisément parce que les deux étages fonctionnent indépendamment – le premier filtre présente une atténuation de 3 dB à la fréquence de coupure, et le second filtre ajoute une autre atténuation de 3 dB.

La limitation fondamentale du filtre RC passe-bas de deuxième ordre est que le concepteur ne peut pas régler avec précision la transition entre la bande passante et la bande d’arrêt en ajustant le facteur Q du filtre ; ce paramètre indique le degré d’amortissement de la réponse en fréquence. Si vous mettez en cascade deux filtres passe-bas RC identiques, la fonction de transfert globale correspond à une réponse du second ordre, mais le facteur Q est toujours de 0,5. Lorsque Q = 0,5, le filtre est à la limite du suramortissement, ce qui se traduit par une réponse en fréquence qui s’affaisse dans la région de transition. Les filtres actifs du second ordre et les filtres du second ordre basés sur la résonance n’ont pas cette limitation ; le concepteur peut contrôler le facteur Q et ainsi affiner la réponse en fréquence dans la région de transition.

Résumé

Tous les signaux électriques contiennent un mélange de composantes de fréquence souhaitées et de composantes de fréquence non souhaitées. Les composantes de fréquence indésirables sont généralement causées par le bruit et les interférences, et dans certaines situations, elles affecteront négativement les performances du système.
Un filtre est un circuit qui réagit de différentes manières à différentes parties du spectre d’un signal. Un filtre passe-bas est conçu pour laisser passer les composantes à basse fréquence et bloquer les composantes à haute fréquence.
La fréquence de coupure d’un filtre passe-bas indique la région de fréquence dans laquelle le filtre passe d’une faible atténuation à une atténuation importante.
La tension de sortie d’un filtre passe-bas RC peut être calculée en traitant le circuit comme un diviseur de tension constitué d’une résistance (indépendante de la fréquence) et d’une réactance (dépendante de la fréquence).
Un tracé de l’amplitude (en dB, sur l’axe vertical) en fonction de la fréquence logarithmique (en hertz, sur l’axe horizontal) est un moyen pratique et efficace d’examiner le comportement théorique d’un filtre. Vous pouvez également utiliser un tracé de la phase en fonction de la fréquence logarithmique pour déterminer la quantité de déphasage qui sera appliquée à un signal d’entrée.
Un filtre de deuxième ordre fournit un roll-off plus raide ; cette réponse de deuxième ordre est utile lorsqu’un signal ne fournit pas une large bande de séparation entre les composantes de fréquence souhaitées et les composantes de fréquence non souhaitées.
Vous pouvez créer un filtre passe-bas RC de deuxième ordre en construisant deux filtres passe-bas RC identiques de premier ordre, puis en connectant la sortie de l’un à l’entrée de l’autre. La fréquence globale de -3 dB sera plus basse que prévu.