Solving the Königsberg Bridge Problem
This proof is accessible to ANYONE — no mathematics knowledge required! (perfect for if you are a bit bored and in isolation, like me right now!)
The Königsberg bridge problem shows the beauty of mathematics to transform the impossible to the obvious. It also gives an insight into the mind of the genius Leonhard Euler.

Stating the problem
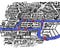
Have a look at the map above.
It’s a diagram of the rivers and bridges of Königsberg. The areas A, B, C and D are bits of land, joined by the bridges, but otherwise cut off from each other by water.
A map of the city is below. Vous pouvez regarder l’un ou l’autre des diagrammes – les deux capturent les éléments d’information essentiels : quels bouts de terre sont reliés à quels autres bouts de terre, et par combien de ponts.
En langage technique, nous représentons ceci comme un graphique. Les blobs de terre sont les sommets, et les ponts sont les arêtes. Mais ce n’est pas important.
Le problème est de savoir s’il est possible de trouver un itinéraire qui passe par chaque pont exactement une fois. Cela signifie que, dans notre promenade dans la ville, nous voulons que notre itinéraire passe par chaque pont, mais il ne peut pas le traverser deux fois, ou trois fois… En gros, si vous vous retrouvez sur le même pont que précédemment, le chemin est invalide. Si vous terminez votre promenade et qu’il y a un pont que vous n’avez pas traversé, alors votre chemin n’était pas valide.
La solution
Considérez chaque blob de terre. Chaque pont est relié à deux blobs de terre (c’est ainsi que les ponts fonctionnent). Il se trouve que chaque blob de terre a un nombre impair de ponts attachés.
Maintenant, considérons à quoi ressemblerait une promenade valide.
Au fur et à mesure de votre promenade, vous notez dans un bloc-notes chaque fois que vous êtes dans un certain blob de terre. Par exemple, si vous commencez dans l’extrémité la plus méridionale de la ville, vous le notez (prenez une photo, achetez un souvenir…) et si vous vous y retrouvez, vous portez à deux le décompte pour le secteur sud.
Pour chaque blob de terre, il y a deux cas
(1) c’est une section de la ville dans laquelle nous ne commençons pas notre promenade, et nous n’y finissons pas notre promenade
(2) c’est une section de la ville dans laquelle soit nous commençons notre promenade, soit nous finissons notre promenade, soit les deux.
Il est clair qu’il y a au plus 2 sections de la ville du deuxième type. Nous ne pouvons pas commencer à deux endroits à la fois, ni finir à deux endroits à la fois.
Comme il y a quatre sections de la ville, cela signifie qu’il y a au moins deux sections de la ville, dans notre promenade, dans lesquelles nous ne finissons ni ne commençons. Choisissons l’une d’entre elles.
Chaque fois que nous entrons dans ce secteur, nous utilisons un pont, et chaque fois que nous le quittons, nous en utilisons un autre. Mais, chaque secteur a un nombre impair de ponts qui lui sont rattachés ! C’est une contradiction. Pour voir pourquoi, rappelons que chaque secteur a soit 3 ponts, soit il a 5 ponts attachés.
Si nous sommes dans le secteur une fois, nous ne pouvons utiliser que deux de ses ponts. Si nous y sommes deux fois, nous utiliserions quatre de ses ponts (ou serions à court de ponts, s’il n’en avait que trois). Si nous y entrons trois fois, nous aurons besoin de six ponts, ce que nous ne pouvons pas avoir. Ainsi, l’exigence selon laquelle nous devons à la fois entrer et sortir d’un secteur de la ville qui n’est ni notre point de départ ni notre point d’arrivée contredit le fait que le nombre de ponts de liaison est impair pour chaque secteur.