Types d’interpolation – Avantages et inconvénients
Méthodes d’interpolation
L’interpolation consiste à utiliser des points dont les valeurs sont connues ou des points échantillons pour estimer des valeurs à d’autres points inconnus. Elle peut être utilisée pour prédire des valeurs inconnues pour n’importe quelles données géographiques ponctuelles, telles que l’élévation, les précipitations, les concentrations chimiques, les niveaux de bruit, et ainsi de suite.
Les méthodes d’interpolation disponibles sont énumérées ci-dessous.
Inverse Distance Weighted (IDW)
L’interpolateur Inverse Distance Weighting suppose que chaque point d’entrée a une influence locale qui diminue avec la distance. Il pondère davantage les points proches de la cellule de traitement que ceux qui en sont plus éloignés. Un nombre spécifié de points, ou tous les points dans un rayon spécifié, peuvent être utilisés pour déterminer la valeur de sortie de chaque emplacement. L’utilisation de cette méthode suppose que l’influence de la variable cartographiée diminue avec la distance par rapport à son emplacement échantillonné.
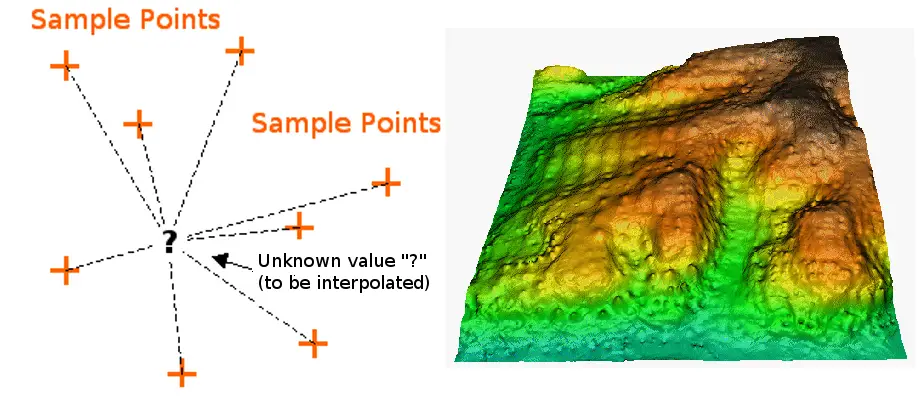
Interpolation IDW ; Courtoisie : QGIS
L’algorithme de pondération de la distance inverse (IDW) est effectivement un interpolateur de moyenne mobile qui est généralement appliqué à des données très variables. Pour certains types de données, il est possible de retourner sur le site de collecte et d’enregistrer une nouvelle valeur qui est statistiquement différente de la lecture originale, mais dans la tendance générale de la zone.
La surface interpolée, estimée par une technique de moyenne mobile, est inférieure à la valeur maximale locale et supérieure à la valeur minimale locale.

Surface interpolée IDW ; Courtesy :ESRI
L’interpolation IDW met explicitement en œuvre l’hypothèse selon laquelle les choses proches les unes des autres sont plus semblables que celles qui sont plus éloignées. Pour prédire une valeur pour un emplacement non mesuré, IDW utilisera les valeurs mesurées entourant l’emplacement de prédiction. Les valeurs mesurées les plus proches de l’emplacement de prédiction auront plus d’influence sur la valeur prédite que celles qui sont plus éloignées. Ainsi, la fonction IDW suppose que chaque point mesuré a une influence locale qui diminue avec la distance. La fonction IDW doit être utilisée lorsque l’ensemble des points est suffisamment dense pour capturer l’étendue de la variation locale de la surface nécessaire à l’analyse. La fonction IDW détermine les valeurs des cellules à l’aide d’un ensemble de points d’échantillonnage combinés avec une pondération linéaire. Elle pondère davantage les points plus proches de l’emplacement de prédiction que ceux qui en sont plus éloignés, d’où le nom de distance inverse pondérée.
La technique IDW calcule une valeur pour chaque nœud de grille en examinant les points de données environnants qui se trouvent dans un rayon de recherche défini par l’utilisateur. Une partie ou la totalité des points de données peuvent être utilisés dans le processus d’interpolation. La valeur du nœud est calculée en faisant la moyenne de la somme pondérée de tous les points. Les points de données qui se trouvent progressivement plus loin du nœud influencent beaucoup moins la valeur calculée que ceux qui se trouvent plus près du nœud.
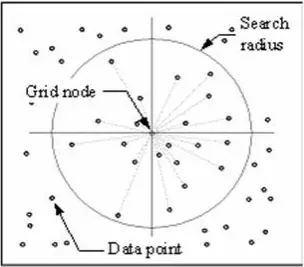
Un rayon est généré autour de chaque nœud de grille à partir duquel les points de données sont sélectionnés pour être utilisés dans le calcul. Options to control the use of IDW include power, search radius, fixed search radius, variable search radius and barrier.
Note: The optimal power (p) value is determined by minimizing the root mean square prediction error (RMSPE).
Advantages
- Can estimate extreme changes in terrain such as: Cliffs, Fault Lines.
- Dense evenly space points are well interpolated (flat areas with cliffs).
- Can increase or decrease amount of sample points to influence cell values.
Disadvantages
- Cannot estimate above maximum or below minimum values.
- Not very good for peaks or mountainous areas.
Natural Neighbour Inverse Distance Weighted (NNIDW)
Natural neighbor interpolation has many positive features, can be used for both interpolation and extrapolation, and generally works well with clustered scatter points. Autre méthode de moyenne pondérée, l’équation de base utilisée dans l’interpolation par les voisins naturels est identique à celle utilisée dans l’interpolation IDW. Cette méthode peut traiter efficacement de grands ensembles de données de points d’entrée. Lors de l’utilisation de la méthode Natural Neighbor, les coordonnées locales définissent la quantité d’influence que tout point de dispersion aura sur les cellules de sortie.
La méthode Natural Neighbour est une technique d’estimation géométrique qui utilise des régions de voisinage naturel générées autour de chaque point de l’ensemble de données.
Comme IDW, cette méthode d’interpolation est une méthode d’interpolation à moyenne pondérée. Cependant, au lieu de trouver la valeur d’un point interpolé en utilisant tous les points d’entrée pondérés par leur distance, l’interpolation Natural Neighbors crée une triangulation de Delauney des points d’entrée et sélectionne les nœuds les plus proches qui forment une coque convexe autour du point d’interpolation, puis pondère leurs valeurs en fonction de la surface proportionnelle. Cette méthode est la plus appropriée lorsque les points de données de l’échantillon sont distribués avec une densité inégale. Il s’agit d’une bonne technique d’interpolation à usage général qui présente l’avantage de ne pas avoir à spécifier de paramètres tels que le rayon, le nombre de voisins ou les pondérations.

Natural IDW : Courtesy : ESRI
Cette technique est conçue pour honorer les valeurs minimales et maximales locales dans le fichier de points et peut être paramétrée pour limiter les dépassements des valeurs hautes locales et les sous-succès des valeurs basses locales. La méthode permet ainsi la création de modèles de surface précis à partir d’ensembles de données qui sont très peu distribués ou très linéaires dans la distribution spatiale.
Avantages
- Gère efficacement un grand nombre de points d’échantillonnage.
Spline
Spline estime les valeurs à l’aide d’une fonction mathématique qui minimise la courbure globale de la surface, ce qui donne une surface lisse qui passe exactement par les points d’entrée.

Spline : Courtesy : ESRI
Conceptuellement, elle est analogue à la courbure d’une feuille de caoutchouc pour passer par des points connus tout en minimisant la courbure totale de la surface. Elle ajuste une fonction mathématique à un nombre spécifié de points d’entrée les plus proches tout en passant par les points d’échantillonnage. Cette méthode est la meilleure pour les surfaces variant doucement, comme l’élévation, la hauteur des nappes phréatiques ou les concentrations de pollution.
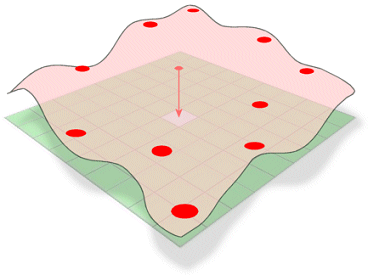
La méthode d’interpolation Spline estime des valeurs inconnues en courbant une surface par des valeurs connues.
Il existe deux méthodes splines : régularisée et de tension.
Une méthode régularisée crée une surface lisse, changeant progressivement avec des valeurs qui peuvent se trouver en dehors de la plage de données de l’échantillon. Elle intègre la première dérivée (pente), la deuxième dérivée (taux de variation de la pente) et la troisième dérivée (taux de variation de la deuxième dérivée) dans ses calculs de minimisation.
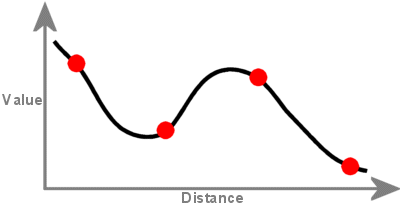
Une surface créée avec une interpolation Spline passe par chaque point d’échantillonnage et peut dépasser la plage de valeurs de l’ensemble de points d’échantillonnage.
Bien qu’une Spline de tension n’utilise que les dérivées premières et secondes, elle inclut plus de points dans les calculs Spline, ce qui crée généralement des surfaces plus lisses mais augmente le temps de calcul.
Cette méthode tire une surface sur les points acquis, ce qui donne un effet étiré. Spline utilise des lignes courbes (méthode Curvilinear Lines) pour calculer les valeurs des cellules.
Choisir un poids pour les interpolations Spline
Spline régularisée : Plus le poids est élevé, plus la surface est lisse. Des poids compris entre 0 et 5 conviennent. Les valeurs typiques sont 0, .001, .01, .1, et .5.
Canal de tension : Plus le poids est élevé, plus la surface est grossière et plus les valeurs sont conformes à la plage de données de l’échantillon. Les valeurs de poids doivent être supérieures ou égales à zéro. Typical values are 0, 1, 5, and 10.
Advantages
- Useful for estimating above maximum and below minimum points.
- Creates a smooth surface effect.
Disadvantages
- Cliffs and fault lines are not well presented because of the smoothing effect.
- When the sample points are close together and have extreme differences in value, Spline interpolation doesn’t work as well. This is because Spline uses slope calculations (change over distance) to figure out the shape of the flexible rubber sheet.
Kriging
Kriging is a geostatistical interpolation technique that considers both the distance and the degree of variation between known data points when estimating values in unknown areas. A kriged estimate is a weighted linear combination of the known sample values around the point to be estimated.
Procédure de krigeage qui génère une surface estimée à partir d’un ensemble dispersé de points avec des valeurs z. Le krigeage suppose que la distance ou la direction entre les points d’échantillonnage reflète une corrélation spatiale qui peut être utilisée pour expliquer la variation de la surface. L’outil de krigeage adapte une fonction mathématique à un nombre spécifié de points, ou à tous les points dans un rayon spécifié, afin de déterminer la valeur de sortie pour chaque emplacement. Le krigeage est un processus en plusieurs étapes ; il comprend l’analyse statistique exploratoire des données, la modélisation du variogramme, la création de la surface et (en option) l’exploration d’une surface de variance. Le krigeage est le plus approprié lorsque vous savez qu’il existe une distance corrélée dans l’espace ou un biais directionnel dans les données. Il est souvent utilisé en pédologie et en géologie.
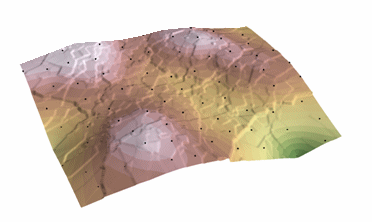
Krigeage : Courtesy: ESRI
The predicted values are derived from the measure of relationship in samples using sophisticated weighted average technique. It uses a search radius that can be fixed or variable. The generated cell values can exceed value range of samples, and the surface does not pass through samples.
The Kriging Formula
Kriging is similar to IDW in that it weights the surrounding measured values to derive a prediction for an unmeasured location. The general formula for both interpolators is formed as a weighted sum of the data:
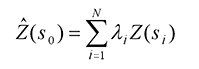
- where:
Z(si) = the measured value at the ith location
λi = an unknown weight for the measured value at the ith location
s0 = the prediction location
N = the number of measured values
In IDW, the weight, λi, depends solely on the distance to the prediction location. Cependant, avec la méthode de krigeage, les poids sont basés non seulement sur la distance entre les points mesurés et l’emplacement de prédiction, mais aussi sur l’arrangement spatial global des points mesurés. Pour utiliser la disposition spatiale dans les pondérations, l’autocorrélation spatiale doit être quantifiée. Ainsi, dans le krigeage ordinaire, le poids, λi, dépend d’un modèle ajusté aux points mesurés, de la distance à l’emplacement de prédiction, et des relations spatiales entre les valeurs mesurées autour de l’emplacement de prédiction. Les sections suivantes traitent de la façon dont la formule générale de krigeage est utilisée pour créer une carte de la surface de prédiction et une carte de la précision des prédictions.
Types de krigeage
Krigeage ordinaire
Le krigeage ordinaire suppose le modèle
Z(s) = µ + ε(s),
où µ est une constante inconnue. L’une des principales questions concernant le krigeage ordinaire est de savoir si l’hypothèse d’une moyenne constante est raisonnable. Sometimes there are good scientific reasons to reject this assumption. However, as a simple prediction method, it has remarkable flexibility.
Ordinary kriging can use either semivariograms or covariances, use transformations and remove trends, and allow for measurement error.
Simple Kriging
Simple kriging assumes the model
Z(s) = µ + ε(s),
where µ is a known constant.
Simple kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Universal Kriging
Universal kriging assumes the model
Z(s) = µ(s) + ε(s),
where µ(s) is some deterministic function.
Universal kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Krigeage indicateur
Le krigeage indicateur suppose le modèle
I(s) = µ + ε(s),
où µ est une constante inconnue et I(s) est une variable binaire. La création de données binaires peut se faire par l’utilisation d’un seuil pour les données continues, ou il se peut que les données observées soient 0 ou 1. Par exemple, vous pouvez avoir un échantillon qui consiste à savoir si un point est un habitat forestier ou non forestier, où la variable binaire indique l’appartenance à une classe. En utilisant des variables binaires, le krigeage indicateur procède de la même manière que le krigeage ordinaire.
Le krigeage indicateur peut utiliser des semivariogrammes ou des covariances.
Krigeage probabiliste
Le krigeage probabiliste suppose le modèle
I(s) = I(Z(s) > ct) = µ1 + ε1(s)Z(s) = µ2 + ε2(s),
où µ1 et µ2 sont des constantes inconnues et I(s) est une variable binaire créée en utilisant un indicateur de seuil, I(Z(s) > ct). Remarquez que maintenant il y a deux types d’erreurs aléatoires, ε1(s) et ε2(s), il y a donc une autocorrélation pour chacune d’elles et une corrélation croisée entre elles. Le krigeage probabiliste s’efforce de faire la même chose que le krigeage indicateur, mais il utilise le cokrigeage dans le but de faire un meilleur travail.
Le krigeage probabiliste peut utiliser soit des semivariogrammes, soit des covariances, des covariances croisées et des transformations, mais il ne peut pas tenir compte de l’erreur de mesure.
style= »display:inline-block;width:468px;height :60px » data-ad-client= »ca-pub-7134201556760050″ data-ad-slot= »9271753327″>
Krigeage disjonctif
Le krigeage disjonctif suppose que le modèle
f(Z(s)) = µ1 + ε(s),
où µ1 est une constante inconnue et f(Z(s)) est une fonction arbitraire de Z(s). Remarquez que vous pouvez écrire f(Z(s)) = I(Z(s) > ct), donc le krigeage indicateur est un cas particulier de krigeage disjonctif. Dans Geostatistical Analyst, vous pouvez prédire soit la valeur elle-même, soit un indicateur avec le krigeage disjonctif.
En général, le krigeage disjonctif essaie de faire plus que le krigeage ordinaire. Si les récompenses peuvent être plus importantes, les coûts le sont aussi. Disjunctive kriging requires the bivariate normality assumption and approximations to the functions fi(Z(si)); the assumptions are difficult to verify, and the solutions are mathematically and computationally complicated.
Disjunctive kriging can use either semivariograms or covariances and transformations, but it cannot allow for measurement error.
Advantages
- Directional influences can be accounted for: Soil Erosion, Siltation Flow, Lava Flow and Winds.
- Exceeds the minimum and maximum point values
Disadvantages
- Does not pass through any of the point values and causes interpolated values to be higher or lower then real values.
** Pour avoir un aperçu approfondi de l’approche mathématique sur le Krigeage, veuillez cliquer sur Krigeage une méthode d’interpolation.
PointInterp
Une méthode qui est similaire à IDW, la fonction PointInterp permet un plus grand contrôle sur le voisinage d’échantillonnage. L’influence d’un échantillon particulier sur la valeur de la cellule de grille interpolée dépend du fait que le point d’échantillonnage se trouve dans le voisinage de la cellule et de la distance qui le sépare de la cellule interpolée. Les points situés en dehors du voisinage n’ont aucune influence.

PointInterp ; Courtesy : ESRI
La valeur pondérée des points à l’intérieur du voisinage est calculée à l’aide d’une interpolation pondérée par distance inverse ou interpolation par distance exponentielle inverse. Cette méthode interpole un raster en utilisant des caractéristiques ponctuelles mais permet différents types de voisinages. Les voisinages peuvent avoir des formes telles que des cercles, des rectangles, des polygones irréguliers, des anneaux ou des coins.
Tendance
La tendance est une méthode statistique qui trouve la surface qui s’adapte aux points de l’échantillon en utilisant un ajustement par régression des moindres carrés. Elle ajuste une équation polynomiale à l’ensemble de la surface. Il en résulte une surface qui minimise la variance de la surface par rapport aux valeurs d’entrée. La surface est construite de manière à ce que, pour chaque point d’entrée, le total des différences entre les valeurs réelles et les valeurs estimées (c’est-à-dire la variance) soit le plus petit possible.

Trend ; Courtsey:ESRI
C’est un interpolateur inexact, et la surface résultante passe rarement par les points d’entrée. Cependant, cette méthode détecte les tendances dans les données de l’échantillon et est similaire aux phénomènes naturels qui varient généralement de manière régulière.
Avantage
- Les surfaces de tendance sont bonnes pour identifier les modèles à grande échelle dans les données ; la surface interpolée passe rarement par les points de l’échantillon.
Topo to Raster
En interpolant les valeurs d’élévation pour un raster, la méthode Topo to Raster impose des contraintes qui garantissent un modèle numérique d’élévation hydrologiquement correct qui contient une structure de drainage connectée et représente correctement les crêtes et les cours d’eau à partir des données de contour d’entrée. Elle utilise une technique d’interpolation itérative par différences finies qui optimise l’efficacité de calcul de l’interpolation locale sans perdre la continuité de surface de l’interpolation globale. Il a été spécifiquement conçu pour travailler intelligemment avec les entrées de contour.
Vous trouverez ci-dessous un exemple de surface interpolée à partir de points d’élévation, de lignes de contour, de lignes de cours d’eau et de polygones de lac à l’aide de l’interpolation Topo to Raster.
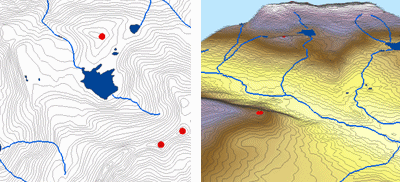
Topo to raster ; Courtesy : ESRI
Topo to Raster est un outil spécialisé pour créer des surfaces matricielles hydrologiquement correctes à partir de données vectorielles de composants de terrain tels que des points d’élévation, des courbes de niveau, des lignes de cours d’eau, des polygones de lacs, des points de puits et des polygones de limites de zones d’étude.
Densité
Les outils de densité (disponibles dans ArcGIS) produisent une surface qui représente la quantité ou le nombre d’une certaine chose par unité de surface. L’outil de densité est utile pour créer des surfaces de densité afin de représenter la distribution d’une population faunique à partir d’un ensemble d’observations, ou le degré d’urbanisation d’une zone en fonction de la densité des routes.

Density Raster; Courtest: ERSI
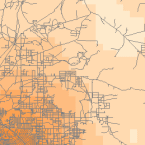
Density and Roads; Courtesy: ESRI
There are density tools for point and line features in ArcGIS.
Related Topics
- What is Interpolation ?
- Classification of Interpolation Techniques.
- Choosing the Right Interpolation Method