Che cos’è il trucco del kernel? Perché è importante?

Quando si parla di kernel nell’apprendimento automatico, molto probabilmente la prima cosa che vi viene in mente è il modello SVM (Support Vector Machine) perché il trucco del kernel è ampiamente usato nel modello SVM per collegare linearità e non linearità.

Per aiutarvi a capire cos’è un kernel e perché è importante, introdurrò prima le basi del modello SVM.

Il modello SVM è un modello di apprendimento automatico supervisionato che viene usato principalmente per le classificazioni (ma potrebbe essere usato anche per la regressione!). Impara a separare i diversi gruppi formando dei confini decisionali.

Nel grafico sopra, si nota che ci sono due classi di osservazioni: i punti blu e i punti viola. Ci sono tonnellate di modi per separare queste due classi, come mostrato nel grafico a sinistra. Tuttavia, vogliamo trovare il “miglior” iperpiano che possa massimizzare il margine tra queste due classi, il che significa che la distanza tra l’iperpiano e i punti dati più vicini su ogni lato è la più grande. A seconda del lato dell’iperpiano in cui si trova un nuovo punto dati, potremmo assegnare una classe alla nuova osservazione.

Sembra semplice nell’esempio precedente. Tuttavia, non tutti i dati sono linearmente separabili. Infatti, nel mondo reale, quasi tutti i dati sono distribuiti in modo casuale, il che rende difficile separare linearmente classi diverse.

Perché è importante usare il trucco del kernel?

Come potete vedere nell’immagine qui sopra, se troviamo un modo per mappare i dati dallo spazio bidimensionale allo spazio tridimensionale, saremo in grado di trovare una superficie decisionale che divide chiaramente tra diverse classi. Il mio primo pensiero di questo processo di trasformazione dei dati è quello di mappare tutti i dati in una dimensione superiore (in questo caso, 3 dimensioni), trovare il confine e fare la classificazione.

Sembra giusto. Tuttavia, quando ci sono sempre più dimensioni, i calcoli all’interno di quello spazio diventano sempre più costosi. È qui che entra in gioco il trucco del kernel. Ci permette di operare nello spazio delle caratteristiche originali senza calcolare le coordinate dei dati in uno spazio dimensionale superiore.

Guardiamo un esempio:

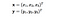
Qui x e y sono due punti dati in 3 dimensioni. Supponiamo che abbiamo bisogno di mappare x e y nello spazio a 9 dimensioni. Dobbiamo fare i seguenti calcoli per ottenere il risultato finale, che è solo uno scalare. La complessità computazionale, in questo caso, è O(n²).

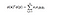
However, if we use the kernel function, which is denoted as k(x, y), instead of doing the complicated computations in the 9-dimensional space, we reach the same result within the 3-dimensional space by calculating the dot product of x -transpose and y. The computational complexity, in this case, is O(n).

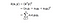
In essence, what the kernel trick does for us is to offer a more efficient and less expensive way to transform data into higher dimensions. With that saying, the application of the kernel trick is not limited to the SVM algorithm. Qualsiasi calcolo che coinvolge i prodotti di punti (x, y) può utilizzare il trucco del kernel.

Diverse funzioni kernel

Ci sono diversi kernel. I più popolari sono il kernel polinomiale e il kernel a funzione base radiale (RBF).

“Intuitivamente, il kernel polinomiale guarda non solo le caratteristiche date dei campioni di input per determinare la loro somiglianza, ma anche le combinazioni di queste” (Wikipedia), proprio come l’esempio sopra. Con n caratteristiche originali e d gradi di polinomio, il kernel polinomiale produce n^d caratteristiche espanse.

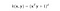
Il kernel RBF è anche chiamato kernel gaussiano. C’è un numero infinito di dimensioni nello spazio delle caratteristiche perché può essere espanso dalla serie di Taylor. Nel formato sottostante, il parametro γ definisce quanta influenza ha un singolo esempio di allenamento. Più è grande, più gli altri esempi devono essere vicini per essere influenzati (documentazione sklearn).

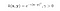
Ci sono diverse opzioni per le funzioni del kernel nella libreria sklearn in Python. Si può anche costruire un kernel personalizzato se necessario.

La fine

Il trucco del kernel sembra un piano “perfetto”. Tuttavia, una cosa critica da tenere a mente è che quando mappiamo i dati in una dimensione più alta, ci sono possibilità che possiamo sovrastimare il modello. Quindi la scelta della giusta funzione kernel (compresi i giusti parametri) e la regolarizzazione sono di grande importanza.

Se siete curiosi di sapere cos’è la regolarizzazione, ho scritto un articolo che parla della mia comprensione di essa e potete trovarlo qui.

Spero che questo articolo vi sia piaciuto. Come sempre, fatemi sapere se avete domande, commenti, suggerimenti, ecc. Grazie per aver letto 🙂