Che cos’è un filtro passa basso? Un tutorial sulle basi dei filtri passivi RC

Dicembre 5, 2021admin

Che cos’è il filtraggio? Impara cosa sono i filtri passa-basso resistore-capacitore (RC) e dove puoi usarli.

Questo articolo introduce il concetto di filtraggio e spiega in dettaglio lo scopo e le caratteristiche dei filtri passa-basso resistore-capacitore (RC).

Dominio del tempo e della frequenza

Quando guardi un segnale elettrico su un oscilloscopio, vedi una linea che rappresenta i cambiamenti di tensione rispetto al tempo. In qualsiasi momento specifico nel tempo, il segnale ha un solo valore di tensione. Quello che si vede sull’oscilloscopio è la rappresentazione del dominio del tempo del segnale.

Una tipica traccia di oscilloscopio è semplice e intuitiva, ma è anche un po’ restrittiva, perché non rivela direttamente il contenuto di frequenza di un segnale. In contrasto con la rappresentazione nel dominio del tempo, in cui un momento nel tempo corrisponde a un solo valore di tensione, una rappresentazione nel dominio della frequenza (chiamata anche spettro) trasmette informazioni su un segnale identificando le varie componenti di frequenza che sono contemporaneamente presenti.

Rappresentazioni nel dominio del tempo di una sinusoide (sopra) e di un’onda quadra (sotto).

Rappresentazioni nel dominio della frequenza di una sinusoide (in alto) e di un’onda quadra (in basso).

Cos’è un filtro?

Un filtro è un circuito che rimuove, o “filtra”, una specifica gamma di componenti di frequenza. In altre parole, separa lo spettro del segnale in componenti di frequenza che passeranno e componenti di frequenza che saranno bloccate.

Se non hai molta esperienza con l’analisi nel dominio della frequenza, potresti essere ancora incerto su cosa siano queste componenti di frequenza e come coesistano in un segnale che non può avere più valori di tensione allo stesso tempo. Vediamo un breve esempio che aiuterà a chiarire questo concetto.

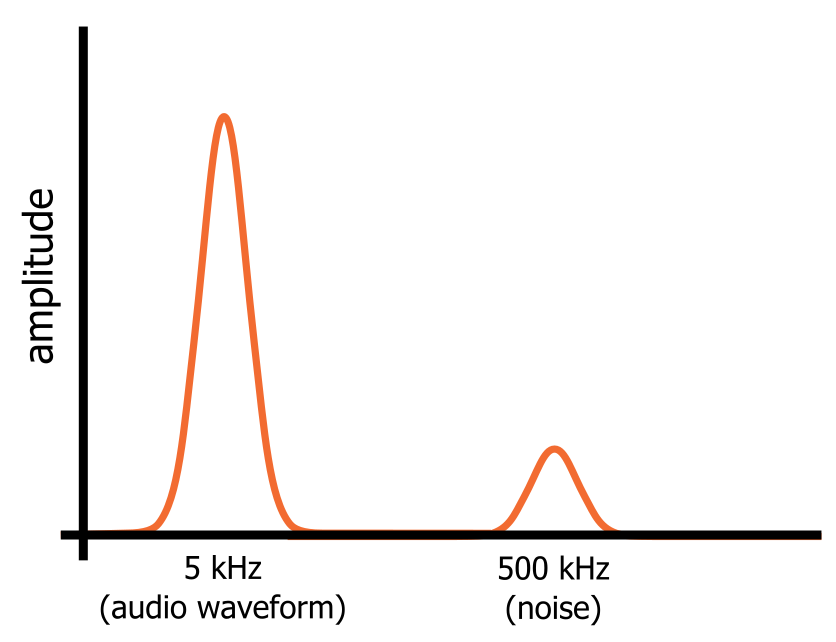
Immaginiamo di avere un segnale audio che consiste in una sinusoide perfetta di 5 kHz. Sappiamo come appare una sinusoide nel dominio del tempo, e nel dominio della frequenza non vedremo altro che un “picco” di frequenza a 5 kHz. Ora supponiamo di attivare un oscillatore a 500 kHz che introduce rumore ad alta frequenza nel segnale audio.

Il segnale visto su un oscilloscopio sarà ancora una sola sequenza di tensioni, con un valore per ogni istante di tempo, ma il segnale avrà un aspetto diverso perché le sue variazioni nel dominio del tempo devono ora riflettere sia la sinusoide a 5 kHz che le fluttuazioni del rumore ad alta frequenza.

Nel dominio della frequenza, però, la sinusoide e il rumore sono componenti di frequenza separate che sono presenti contemporaneamente in questo unico segnale. L’onda sinusoidale e il rumore occupano porzioni diverse della rappresentazione del dominio della frequenza del segnale (come mostrato nel diagramma qui sotto), e questo significa che possiamo filtrare il rumore dirigendo il segnale attraverso un circuito che passa le basse frequenze e blocca le alte frequenze.

Tipi di filtri

I filtri possono essere collocati in grandi categorie che corrispondono alle caratteristiche generali della risposta in frequenza del filtro. Se un filtro fa passare le basse frequenze e blocca le alte frequenze, si chiama filtro passa-basso. Se blocca le basse frequenze e fa passare le alte frequenze, è un filtro passa-alto. Ci sono anche filtri passa-banda, che fanno passare solo una gamma relativamente stretta di frequenze, e filtri band-stop, che bloccano solo una gamma relativamente stretta di frequenze.

I filtri possono anche essere classificati in base ai tipi di componenti che vengono utilizzati per implementare il circuito. I filtri passivi utilizzano resistenze, condensatori e induttori; questi componenti non hanno la capacità di fornire un’amplificazione, e di conseguenza un filtro passivo può solo mantenere o ridurre l’ampiezza di un segnale in ingresso. Un filtro attivo, invece, può sia filtrare un segnale che applicare un guadagno, perché include un componente attivo come un transistor o un amplificatore operativo.

Questo filtro passa-basso attivo è basato sulla popolare topologia Sallen-Key.

Questo articolo esplora l’analisi e la progettazione di filtri passivi passa-basso. Questi circuiti giocano un ruolo importante in una grande varietà di sistemi e applicazioni.

Il filtro passa-basso RC

Per creare un filtro passa-basso passivo, abbiamo bisogno di combinare un elemento resistivo con un elemento reattivo. In altre parole, abbiamo bisogno di un circuito che consiste in un resistore e un condensatore o un induttore. In teoria, la topologia passa-basso resistenza-induttore (RL) è equivalente, in termini di capacità di filtraggio, alla topologia passa-basso resistenza-capacitore (RC). In pratica, però, la versione resistenza-capacitore è molto più comune, e di conseguenza il resto di questo articolo si concentrerà sul filtro passa-basso RC.

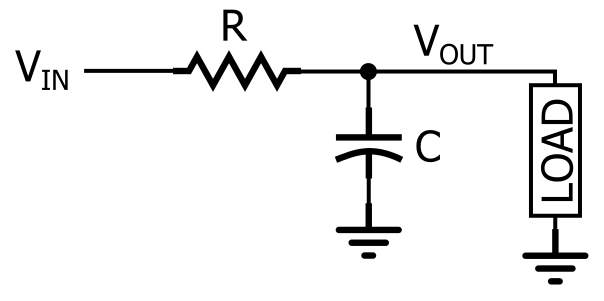
Il filtro passa-basso RC.

Come potete vedere nel diagramma, una risposta passa-basso RC è creata mettendo una resistenza in serie al percorso del segnale e un condensatore in parallelo al carico. Nel diagramma, il carico è un singolo componente, ma in un circuito reale potrebbe essere qualcosa di molto più complicato, come un convertitore analogico-digitale, un amplificatore, o lo stadio di ingresso dell’oscilloscopio che state usando per misurare la risposta del filtro.

Possiamo analizzare intuitivamente l’azione di filtraggio della topologia RC passa-basso se riconosciamo che il resistore e il condensatore formano un divisore di tensione dipendente dalla frequenza.

Il filtro passa-basso RC ridisegnato in modo da sembrare un divisore di tensione.

Quando la frequenza del segnale di ingresso è bassa, l’impedenza del condensatore è alta rispetto all’impedenza del resistore; così, la maggior parte della tensione di ingresso è caduta attraverso il condensatore (e attraverso il carico, che è in parallelo al condensatore). Quando la frequenza di ingresso è alta, l’impedenza del condensatore è bassa rispetto all’impedenza del resistore, il che significa che più tensione è caduta attraverso il resistore e meno è trasferita al carico. Così, le basse frequenze passano e le alte frequenze vengono bloccate.

Questa spiegazione qualitativa della funzionalità RC passa-basso è un primo passo importante, ma non è molto utile quando dobbiamo effettivamente progettare un circuito, perché i termini “alta frequenza” e “bassa frequenza” sono estremamente vaghi. Gli ingegneri hanno bisogno di creare circuiti che passano e bloccano frequenze specifiche. Per esempio, nel sistema audio descritto sopra, vogliamo preservare un segnale di 5 kHz e sopprimere un segnale di 500 kHz. Questo significa che abbiamo bisogno di un filtro che passi dal passaggio al blocco da qualche parte tra 5 kHz e 500 kHz.

La frequenza di taglio

La gamma di frequenze per cui un filtro non causa un’attenuazione significativa è chiamata banda passante, e la gamma di frequenze per cui il filtro causa un’attenuazione significativa è chiamata banda di arresto. I filtri analogici, come il filtro passa-basso RC, passano sempre gradualmente dalla banda passante alla banda di arresto. Questo significa che è impossibile identificare una frequenza alla quale il filtro smette di far passare i segnali e inizia a bloccarli. Tuttavia, gli ingegneri hanno bisogno di un modo per riassumere convenientemente e concisamente la risposta in frequenza di un filtro, ed è qui che entra in gioco il concetto di frequenza di taglio.

Quando si guarda un grafico della risposta in frequenza di un filtro RC, si noterà che il termine “frequenza di taglio” non è molto preciso. L’immagine dello spettro di un segnale che viene “tagliato” in due metà, una delle quali viene mantenuta e una scartata, non si applica, perché l’attenuazione aumenta gradualmente man mano che le frequenze si spostano da sotto il cutoff a sopra il cutoff.

La frequenza di cutoff di un filtro passa-basso RC è in realtà la frequenza alla quale l’ampiezza del segnale di ingresso viene ridotta di 3 dB (questo valore è stato scelto perché una riduzione di 3 dB in ampiezza corrisponde a una riduzione del 50% della potenza). Così, la frequenza di cutoff è anche chiamata la frequenza -3 dB, e in effetti questo nome è più preciso e più informativo. Il termine larghezza di banda si riferisce alla larghezza della banda passante di un filtro, e nel caso di un filtro passa-basso, la larghezza di banda è uguale alla frequenza -3 dB (come mostrato nel diagramma sottostante).

Questo diagramma trasmette le caratteristiche generiche della risposta in frequenza di un filtro passa-basso RC. La larghezza di banda è uguale alla frequenza -3 dB.

Come spiegato sopra, il comportamento passa-basso di un filtro RC è causato dall’interazione tra l’impedenza indipendente dalla frequenza della resistenza e l’impedenza dipendente dalla frequenza del condensatore. Per determinare i dettagli della risposta in frequenza di un filtro, dobbiamo analizzare matematicamente la relazione tra la resistenza (R) e la capacità (C), e possiamo anche manipolare questi valori per progettare un filtro che soddisfi specifiche precise. La frequenza di taglio (fC) di un filtro passa-basso RC si calcola come segue:

Guardiamo un semplice esempio di progettazione. I valori dei condensatori sono più restrittivi dei valori delle resistenze, quindi inizieremo con un valore comune di capacità (come 10 nF), e poi useremo l’equazione per determinare il valore di resistenza richiesto. L’obiettivo è quello di progettare un filtro che preservi una forma d’onda audio di 5 kHz e rifiuti una forma d’onda di rumore di 500 kHz. Proveremo una frequenza di taglio di 100 kHz, e più avanti nell’articolo analizzeremo più attentamente l’effetto di questo filtro sulle due componenti di frequenza.

Quindi, una resistenza da 160 Ω combinata con un condensatore da 10 nF ci darà un filtro che si avvicina molto alla risposta in frequenza desiderata.

Calcolo della risposta del filtro

Possiamo calcolare il comportamento teorico di un filtro passa-basso usando una versione dipendente dalla frequenza di un tipico calcolo del divisore di tensione. L’uscita di un partitore di tensione resistivo è espressa come segue:

Il filtro RC usa una struttura equivalente, ma al posto di R2 abbiamo un condensatore. Per prima cosa, sostituiamo R2 (al numeratore) con la reattanza del condensatore (XC). Poi, dobbiamo calcolare la grandezza dell’impedenza totale e metterla nel denominatore. Così, abbiamo

La reattanza di un condensatore indica la quantità di opposizione al flusso di corrente, ma a differenza della resistenza, la quantità di opposizione dipende dalla frequenza del segnale che passa attraverso il condensatore. Quindi, dobbiamo calcolare la reattanza a una frequenza specifica, e l’equazione che usiamo per questo è la seguente:

Nell’esempio di progettazione sopra, R ≈ 160 Ω e C = 10 nF. Assumeremo che l’ampiezza di VIN sia 1 V, in modo da poter semplicemente rimuovere VIN dal calcolo. Prima calcoliamo l’ampiezza di VOUT alla frequenza della sinusoide:

L’ampiezza della sinusoide è sostanzialmente invariata. Questo è un bene, dato che la nostra intenzione era di preservare l’onda sinusoidale sopprimendo il rumore. Questo risultato non è sorprendente, dato che abbiamo scelto una frequenza di taglio (100 kHz) che è molto più alta della frequenza dell’onda sinusoidale (5 kHz).

Ora vediamo come il filtro riuscirà ad attenuare la componente di rumore.

L’ampiezza del rumore è solo circa il 20% del suo valore originale.

Visualizzare la risposta del filtro

Il mezzo più conveniente per valutare l’effetto di un filtro su un segnale è esaminare un grafico della risposta in frequenza del filtro. Questi grafici, spesso chiamati diagrammi di Bode, hanno la grandezza (in decibel) sull’asse verticale e la frequenza sull’asse orizzontale; l’asse orizzontale ha tipicamente una scala logaritmica, così che la distanza fisica tra 1 Hz e 10 Hz è la stessa della distanza fisica tra 10 Hz e 100 Hz, tra 100 Hz e 1 kHz, e così via. Questa configurazione ci permette di valutare rapidamente e accuratamente il comportamento di un filtro su una gamma molto ampia di frequenze.

Un esempio di grafico frequenza-risposta.

Ogni punto della curva indica la grandezza che il segnale di uscita avrà se il segnale di ingresso ha una grandezza di 1 V e una frequenza uguale al valore corrispondente sull’asse orizzontale. Per esempio, quando la frequenza di ingresso è di 1 MHz, l’ampiezza di uscita (assumendo un’ampiezza di ingresso di 1 V) sarà di 0,1 V (perché -20 dB corrisponde a un fattore di riduzione di dieci).

La forma generale di questa curva frequenza-risposta vi diventerà molto familiare quando passerete più tempo con i circuiti di filtraggio. La curva è quasi perfettamente piatta nella banda passante, e poi comincia a scendere più rapidamente man mano che la frequenza di ingresso si avvicina alla frequenza di taglio. Alla fine il tasso di variazione dell’attenuazione, chiamato roll-off, si stabilizza a 20 dB/decade, cioè la grandezza del segnale di uscita si riduce di 20 dB per ogni aumento di un fattore di dieci nella frequenza di ingresso.

Valutazione delle prestazioni dei filtri passa-basso

Se tracciamo attentamente la risposta in frequenza del filtro che abbiamo progettato in precedenza nell’articolo, vedremo che la risposta in magnitudine a 5 kHz è essenzialmente 0 dB (cioè, quasi zero attenuazione) e la risposta di grandezza a 500 kHz è circa -14 dB (che corrisponde a un guadagno di 0,2). Questi valori sono coerenti con i risultati dei calcoli che abbiamo eseguito nella sezione precedente.

Perché i filtri RC hanno sempre una transizione graduale dalla banda passante alla banda di arresto, e perché l’attenuazione non raggiunge mai l’infinito, non possiamo progettare un filtro “perfetto” – cioè un filtro che non ha effetto sulla sinusoide ed elimina completamente il rumore. Invece, abbiamo sempre un compromesso. Se spostiamo la frequenza di taglio più vicino a 5 kHz, avremo più attenuazione del rumore ma anche più attenuazione della sinusoide che vogliamo inviare a un altoparlante. Se spostiamo la frequenza di cutoff più vicino a 500 kHz, avremo meno attenuazione alla frequenza della sinusoide, ma anche meno attenuazione alla frequenza del rumore.

Spostamento di fase del filtro passa-basso

Finora abbiamo discusso il modo in cui un filtro modifica l’ampiezza delle varie componenti di frequenza in un segnale. Tuttavia, gli elementi reattivi del circuito introducono sempre uno spostamento di fase oltre agli effetti di ampiezza.

Il concetto di fase si riferisce al valore di un segnale periodico in un momento specifico all’interno di un ciclo. Così, quando diciamo che un circuito causa uno sfasamento, intendiamo dire che crea un disallineamento tra il segnale di ingresso e il segnale di uscita: i segnali di ingresso e di uscita non iniziano e terminano più i loro cicli nello stesso momento nel tempo. Il valore dello spostamento di fase, come 45° o 90°, indica quanto disallineamento è stato creato.

Ogni elemento reattivo in un circuito introduce 90° di spostamento di fase, ma questo spostamento di fase non avviene tutto in una volta. La fase del segnale di uscita, proprio come la grandezza del segnale di uscita, cambia gradualmente all’aumentare della frequenza di ingresso. In un filtro passa-basso RC, abbiamo un elemento reattivo (il condensatore), e di conseguenza il circuito alla fine introdurrà 90° di sfasamento.

Come per la risposta di grandezza, la risposta di fase è più facilmente valutabile esaminando un grafico in cui l’asse orizzontale indica la frequenza logaritmica. La descrizione che segue trasmette il modello generale, e poi potete riempire i dettagli esaminando il grafico.

Lo spostamento di fase è inizialmente di 0°.
Aumenta gradualmente fino a raggiungere 45° alla frequenza di taglio; durante questa parte della risposta, il tasso di cambiamento è crescente.
Dopo la frequenza di taglio, lo spostamento di fase continua ad aumentare, ma il tasso di cambiamento è in diminuzione.
Il tasso di cambiamento diventa molto piccolo come lo spostamento di fase si avvicina asintoticamente a 90°.

La linea continua è la risposta di grandezza, e la linea tratteggiata è la risposta di fase. La frequenza di cutoff è 100 kHz. Notate che lo spostamento di fase è di 45° alla frequenza di cutoff.

Filtri passa-basso di secondo ordine

Finora abbiamo assunto che un filtro passa-basso RC consiste di un resistore e un condensatore. Questa configurazione è un filtro del primo ordine.

L'”ordine” di un filtro passivo è determinato dal numero di elementi reattivi – cioè, condensatori o induttori – che sono presenti nel circuito. Un filtro di ordine superiore ha più elementi reattivi, e questo porta a un maggiore spostamento di fase e a un roll-off più ripido. Questa seconda caratteristica è la motivazione principale per aumentare l’ordine di un filtro.

Aggiungendo un elemento reattivo a un filtro – per esempio, passando dal primo al secondo ordine o dal secondo al terzo – aumentiamo il roll-off massimo di 20 dB/decade. Un roll-off più ripido si traduce in una transizione più rapida dalla bassa attenuazione all’alta attenuazione, e questo può portare a prestazioni migliori quando il segnale non ha un’ampia banda di frequenza che separa le componenti di frequenza desiderate dalle componenti di rumore.

I filtri del secondo ordine sono comunemente costruiti intorno a un circuito risonante costituito da un induttore e un condensatore (questa topologia è chiamata “RLC” per resistenza-induttore-capacitore). Tuttavia, è anche possibile creare filtri RC del secondo ordine. Come mostrato nel diagramma qui sotto, tutto quello che dobbiamo fare è mettere in cascata due filtri RC del primo ordine.

Anche se questa topologia crea certamente una risposta del secondo ordine, non è molto usata – come vedremo nella prossima sezione, la risposta in frequenza è spesso inferiore a quella di un filtro attivo del secondo ordine o un filtro RLC del secondo ordine.

Risposta in frequenza del filtro RC del secondo ordine

Possiamo tentare di creare un filtro passa-basso RC del secondo ordine progettando un filtro del primo ordine secondo la frequenza di taglio desiderata e poi collegando due di questi stadi del primo ordine in serie. Questo risulta in un filtro che ha una risposta in frequenza complessiva simile e un roll-off massimo di 40 dB/decade invece di 20 dB/decade.

Tuttavia, se guardiamo la risposta più da vicino, vediamo che la frequenza -3 dB è diminuita. Il filtro RC del secondo ordine non si comporta come previsto perché i due stadi non sono indipendenti – non possiamo semplicemente collegare questi due stadi insieme e analizzare il circuito come un filtro passa-basso del primo ordine seguito da un identico filtro passa-basso del primo ordine.

Inoltre, anche se inseriamo un buffer tra i due stadi, in modo che il primo stadio RC e il secondo stadio RC possano funzionare come filtri indipendenti, l’attenuazione alla frequenza di taglio originale sarà 6 dB invece di 3 dB. Questo accade proprio perché i due stadi funzionano in modo indipendente – il primo filtro ha 3 dB di attenuazione alla frequenza di taglio, e il secondo filtro aggiunge altri 3 dB di attenuazione.

La limitazione fondamentale del filtro passa-basso RC del secondo ordine è che il progettista non può regolare con precisione la transizione dalla banda passante alla banda di arresto regolando il fattore Q del filtro; questo parametro indica quanto è smorzata la risposta in frequenza. Se si mettono in cascata due filtri RC passa-basso identici, la funzione di trasferimento complessiva corrisponde a una risposta del secondo ordine, ma il fattore Q è sempre 0,5. Quando Q = 0,5, il filtro è al limite del sovrasmorzamento, e questo si traduce in una risposta in frequenza che si “affloscia” nella regione di transizione. I filtri attivi del secondo ordine e i filtri basati sulla risonanza del secondo ordine non hanno questa limitazione; il progettista può controllare il fattore Q e quindi regolare con precisione la risposta in frequenza nella regione di transizione.

Sommario

Tutti i segnali elettrici contengono una miscela di componenti di frequenza desiderate e componenti di frequenza indesiderate. Le componenti di frequenza indesiderate sono tipicamente causate da rumore e interferenze, e in alcune situazioni influenzano negativamente le prestazioni del sistema.
Un filtro è un circuito che reagisce in modi diversi alle diverse porzioni dello spettro di un segnale. Un filtro passa-basso è progettato per far passare componenti a bassa frequenza e bloccare componenti ad alta frequenza.
La frequenza di cutoff di un filtro passa-basso indica la regione di frequenza in cui il filtro passa da una bassa attenuazione a un’attenuazione significativa.
La tensione di uscita di un filtro passa-basso RC può essere calcolata trattando il circuito come un divisore di tensione costituito da una resistenza (indipendente dalla frequenza) e una reattanza (dipendente dalla frequenza).
Un grafico della grandezza (in dB, sull’asse verticale) rispetto alla frequenza logaritmica (in hertz, sull’asse orizzontale) è un modo conveniente ed efficace per esaminare il comportamento teorico di un filtro. Si può anche usare un grafico della fase rispetto alla frequenza logaritmica per determinare la quantità di spostamento di fase che sarà applicata a un segnale di ingresso.
Un filtro del secondo ordine fornisce un roll-off più ripido; questa risposta del secondo ordine è utile quando un segnale non fornisce un’ampia banda di separazione tra le componenti di frequenza desiderate e quelle indesiderate.
Si può creare un filtro passa-basso RC del secondo ordine costruendo due identici filtri passa-basso RC del primo ordine e poi collegando l’uscita di uno all’ingresso dell’altro. La frequenza complessiva -3 dB sarà più bassa del previsto.