dB: Cos’è un decibel?

Pressione sonora, livello sonoro e dB. Il suono viene solitamente misurato con i microfoni e questi rispondono proporzionalmente alla pressione sonora, p. Ora la potenza in un’onda sonora, a parità di condizioni, va come il quadrato della pressione. (Allo stesso modo, la potenza elettrica in un resistore va come il quadrato della tensione). Il log di x2 è solo 2 log x, quindi questo introduce un fattore 2 quando convertiamo i rapporti di pressione in decibel. La differenza di livello di pressione sonora tra due suoni con p1 e p2 è quindi:

20 log (p2/p1) dB = 10 log (p22/p12) dB = 10 log (P2/P1) dB (in tutto, il log è in base 10).

Cosa succede quando si dimezza la potenza sonora? Il log di 2 è 0,3010, quindi il log di 1/2 è -0,3, con buona approssimazione. Quindi, se dimezzi la potenza, riduci la potenza e il livello sonoro di 3 dB. Dimezza ancora (fino a 1/4 della potenza originale) e riduci il livello di altri 3 dB. Se continuate a dimezzare la potenza, avrete questi rapporti.

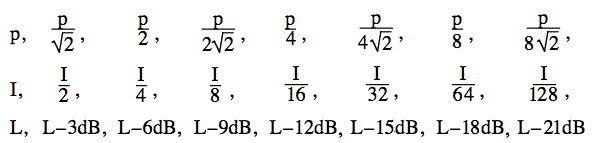
Cosa succede se aggiungo due suoni uguali? Raddoppio l’intensità (aumento di 3 dB)? O raddoppio la pressione (aumento di 6 dB)? Questa domanda frequente è un po’ sottile, quindi è discussa qui sulle nostre FAQ.

File audio per mostrare la grandezza di un decibel

Abbiamo visto sopra che dimezzare la potenza riduce la pressione sonora di √2 e il livello sonoro di 3 dB. Questo è quello che abbiamo fatto nel primo grafico e nel file audio qui sotto.

Il primo campione di suono è rumore bianco (un mix di una vasta gamma di frequenze udibili, analogo alla luce bianca, che è un mix di tutte le frequenze visibili). Il secondo campione è lo stesso rumore, con la tensione ridotta di un fattore √2. Ora 1/√2 è circa 0,7, quindi -3 dB corrisponde a ridurre la tensione o la pressione al 70% del suo valore originale. La linea verde mostra la tensione in funzione del tempo. La linea rossa mostra un decadimento esponenziale continuo con il tempo. Notate che la tensione scende del 50% per ogni secondo campione. Notate anche che un raddoppio della potenza non fa una differenza enorme per il volume. Ne parleremo più avanti, ma è una cosa utile da ricordare quando si scelgono le apparecchiature per la riproduzione del suono. File audio e animazione di John Tann e George Hatsidimitris.

Quanto è grande un decibel? Nella prossima serie, i campioni successivi sono ridotti di un solo decibel.

Un decibel è dello stesso ordine della Just Noticeable Difference (JND) per il livello del suono. Ascoltando questi file, noterete che l’ultimo è più silenzioso del primo, ma è piuttosto meno chiaro all’orecchio che il secondo di ogni coppia è più silenzioso del suo predecessore. 10*log10(1,26) = 1, quindi per aumentare il livello sonoro di 1 dB, la potenza deve essere aumentata del 26%, o la tensione del 12%.

E se la differenza è meno di un decibel? I livelli sonori sono raramente indicati con cifre decimali. La ragione è che i livelli sonori che differiscono di meno di 1 dB sono difficili da distinguere, come mostra il prossimo esempio (questo rende il dB una comoda unità di misura).

0.3 dB steps. Si può notare che l’ultimo è più silenzioso del primo, ma è difficile notare la differenza tra coppie successive. 10*log10(1,07) = 0,3, quindi per aumentare il livello sonoro di 0,3 dB, la potenza deve essere aumentata del 7%, o la tensione del 3,5%.

Livelli di riferimento standard (livello sonoro ‘assoluto’)

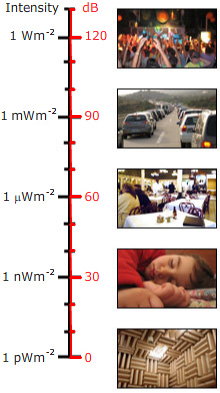Abbiamo detto sopra che il decibel è un rapporto. Quindi, quando viene usato per dare il livello sonoro di un singolo suono piuttosto che un rapporto, bisogna scegliere un livello di riferimento. Per il livello di pressione sonora, il livello di riferimento (per l’aria) è solitamente scelto come pref = 20 micropascal (20 μPa), o 0,02 mPa. Questo è molto basso: è 2 decimiliardesimi di un’atmosfera. Tuttavia, questo è circa il limite della sensibilità dell’orecchio umano, nella sua gamma sensibile di frequenza. (Di solito questa sensibilità si trova solo in persone piuttosto giovani o in persone che non sono state esposte a musica alta o altri rumori forti. I sistemi musicali personali con altoparlanti in-ear sono capaci di livelli sonori molto alti nell’orecchio, e sono ritenuti da alcuni responsabili di gran parte della perdita dell’udito nei giovani adulti in alcuni paesi).

Quindi se leggete di un livello di pressione sonora di 86 dB, significa che

20 log (p2/pref) = 86 dB

dove pref è la pressione sonora del livello di riferimento, e p2 quella del suono in questione. Dividiamo entrambi i lati per 20:

log (p2/pref) = 4,3

p2/pref = 104,3

4 è il log di 10 mila, 0,3 è il log di 2, quindi questo suono ha una pressione sonora 20 mila volte superiore a quella del livello di riferimento (p2/pref = 20.000) o un’intensità 400 milioni di volte l’intensità di riferimento. 86 dB è un suono forte ma non pericoloso, a condizione che l’esposizione sia breve.

Cosa significa 0 dB? Questo livello si verifica quando l’intensità misurata è uguale al livello di riferimento, cioè è il livello sonoro corrispondente a 0,02 mPa. In questo caso abbiamo

livello sonoro = 20 log (pmeasured/pref) = 20 log 1 = 0 dB

Ricorda che i decibel misurano un rapporto. 0 dB si verifica quando si prende il log di un rapporto di 1 (log 1 = 0). Quindi 0 dB non significa nessun suono, significa un livello sonoro in cui la pressione sonora è uguale a quella del livello di riferimento. Si tratta di una pressione piccola, ma non nulla. È anche possibile avere livelli sonori negativi: – 20 dB significherebbe un suono con una pressione 10 volte inferiore a quella di riferimento, cioè 2 μPa.

Non tutte le pressioni sonore sono ugualmente forti. Questo perché l’orecchio umano non risponde allo stesso modo a tutte le frequenze: siamo molto più sensibili ai suoni nella gamma di frequenza da 1 kHz a 7 kHz circa (da 1000 a 7000 vibrazioni al secondo) che ai suoni a frequenza molto bassa o alta. Per questo motivo, i fonometri sono di solito dotati di un filtro la cui risposta alla frequenza è un po’ come quella dell’orecchio umano. (Per saperne di più su questi filtri, vedi sotto.) Se viene usato il “filtro di ponderazione A”, il livello di pressione sonora è dato in unità di dB(A) o dBA. Il livello di pressione sonora sulla scala dBA è facile da misurare ed è quindi ampiamente utilizzato. Uno dei motivi per cui è diverso dalla loudness è che il filtro non risponde allo stesso modo dell’orecchio. Per capire l’intensità di un suono, la prima cosa da fare è consultare alcune curve che rappresentano la risposta in frequenza dell’orecchio umano, date qui sotto. (Un altro motivo è che l’udito umano non è logaritmico.

Misure logaritmiche

Perché usiamo i decibel? L’orecchio è in grado di sentire una gamma molto ampia di suoni: il rapporto tra la pressione sonora che causa danni permanenti da una breve esposizione e il limite che le orecchie (non danneggiate) possono sentire è più di un milione. Per trattare una tale gamma, le unità logaritmiche sono utili: il log di un milione è 6, quindi questo rapporto rappresenta una differenza di 120 dB. L’udito non ha una risposta intrinsecamente logaritmica. (Le misure logaritmiche sono anche utili quando un suono (brevemente) aumenta o diminuisce esponenzialmente nel tempo. Questo accade in molte applicazioni che coinvolgono il guadagno proporzionale o la perdita proporzionale.)

I filtri utilizzati per dBA e dB(C)

Il filtro di livello sonoro più utilizzato è la scala A, che corrisponde approssimativamente all’inverso della curva di equalizzazione a 40 dB (a 1 kHz). Utilizzando questo filtro, il fonometro è quindi meno sensibile alle frequenze molto alte e molto basse. Le misure effettuate su questa scala sono espresse in dBA. La scala C varia poco su diverse ottave ed è quindi adatta per misurazioni soggettive solo per livelli sonori da moderati ad alti. Le misurazioni effettuate su questa scala sono espresse come dB(C). C’è anche una scala di ponderazione B (usata raramente), intermedia tra A e C. La figura qui sotto mostra la risposta del filtro A (a sinistra) e del filtro C, con i guadagni in dB dati rispetto a 1 kHz. (Per un’introduzione ai filtri, vedi Filtri RC, integratori e differenziatori).



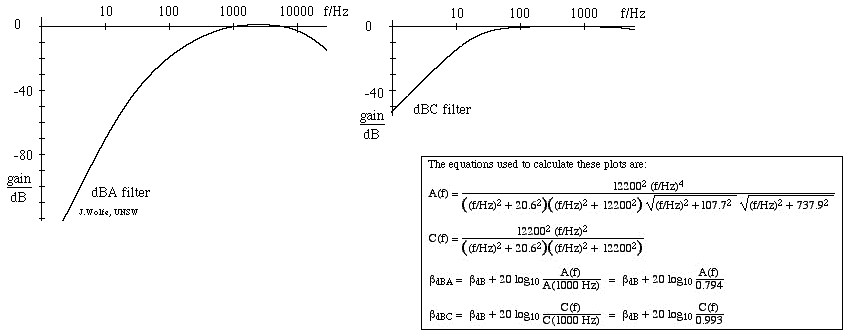
Nei siti di acustica musicale e di acustica del parlato, tracciamo gli spettri sonori in dB. La ragione di questa pratica comune è che la gamma di pressioni sonore misurate è grande.

Le misure di dB(G) usano un filtro a banda stretta che dà un’alta ponderazione alle frequenze tra 1 e 20 Hz, e una bassa ponderazione alle altre. Fornisce quindi grandi valori per i suoni e gli infrasuoni che non sono facilmente udibili. ISO 7196:1995

Loudness, phons e sones, curve di risposta uditiva

Il phon è un’unità che è correlata al dB dalla risposta in frequenza dell’orecchio misurata psicofisicamente. A 1 kHz, le letture in phon e in dB sono, per definizione, le stesse. Per tutte le altre frequenze, la scala phon è determinata dai risultati di esperimenti in cui ai volontari è stato chiesto di regolare l’intensità di un segnale a una data frequenza fino a quando hanno giudicato la sua intensità uguale a quella di un segnale a 1 kHz. Per convertire da dB a phon, è necessario un grafico di tali risultati. Tale grafico dipende dal livello del suono: diventa più piatto a livelli sonori elevati.

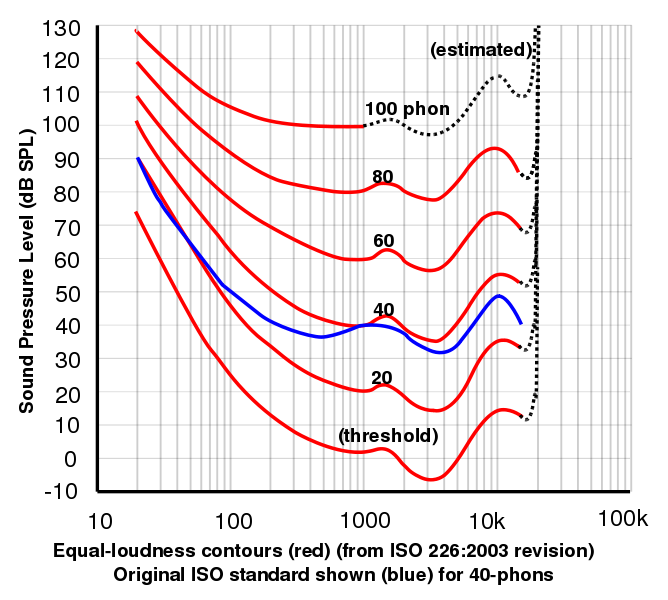
Questo grafico, per gentile concessione di Lindosland, mostra i dati 2003 dell’International Standards Organisation per curve di uguale loudness determinate sperimentalmente. I grafici di loudness uguale in funzione della frequenza sono spesso chiamati genericamente curve di Fletcher-Munson dopo il lavoro originale di Fletcher, H. e Munson, W.A. (1933) J.Acoust.Soc.Am. 6:59. Puoi creare le tue curve usando il nostro sito sulle risposte uditive.

Il sone è derivato da misure psicofisiche che coinvolgono volontari che regolano i suoni fino a giudicarli due volte più forti. Questo permette di mettere in relazione l’intensità percepita con i foni. Un sone è definito come uguale a 40 phon. Sperimentalmente si è scoperto che, al di sopra dei 40 phon, un aumento di 10 dB del livello sonoro corrisponde approssimativamente a un raddoppio della loudness percepita. Così questa approssimazione è usata nella definizione del sone: 1 sone = 40 phon, 2 sone = 50 phon, 4 sone = 60 phon, ecc.



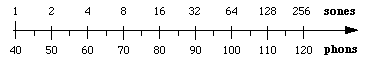
Questa relazione implica che loudness e intensità sono legati da una legge di potenza: loudness in soni è proporzionale a (intensità)log 2 = (intensità)0.3.

Non sarebbe bello poter convertire dai dB (che possono essere misurati da uno strumento) ai soni (che approssimano l’intensità percepita dalle persone)? Questo a volte viene fatto usando delle tabelle che si possono trovare nei manuali di acustica. Comunque, se non ti dispiace un’approssimazione piuttosto rozza, puoi dire che la curva di ponderazione A approssima la risposta in frequenza umana a livelli sonori da bassi a moderati, quindi dB(A) è molto approssimativamente uguale ai phon, su una gamma limitata di bassi livelli. Allora si può usare la relazione logaritmica tra soni e phon descritta sopra.

Livello di registrazione e decibel

I misuratori che misurano il livello di registrazione o di uscita sulle apparecchiature elettroniche audio (console di mixaggio ecc.) registrano quasi sempre la tensione AC rms (vedi i link per scoprire AC e rms). Per una data resistenza R, la potenza P è V2/R, quindi
differenza nel livello di tensione = 20 log (V2/V1) dB = 10 log (V22/V12) dB = 10 log (P2/P1) dB, o

livello di tensione assoluto = 20 log (V/Vref)

dove Vref è una tensione di riferimento. Quindi qual è la tensione di riferimento?

Il livello ovvio da scegliere è un volt rms, e in questo caso il livello è scritto come dBV. Questo è razionale, e anche conveniente con le schede analogico-digitali la cui gamma massima è spesso circa un volt rms. Quindi bisogna ricordarsi di mantenere il livello in dBV negativo (meno di un volt) per evitare di tagliare i picchi del segnale, ma non troppo negativo (così il vostro segnale è ancora molto più grande del rumore di fondo).

A volte vedrete dBm. Questo significava decibel di potenza elettrica, rispetto a un milliwatt, e a volte lo fa ancora. Tuttavia, è complicato per ragioni storiche. A metà del ventesimo secolo, molte linee audio avevano un’impedenza nominale di 600 Ω. Se l’impedenza è puramente resistiva, e se si imposta V2/600 Ω = 1 mW, allora si ottiene V = 0,775 volt. Quindi, ammesso che tu stia usando un carico di 600 Ω, 1 mW di potenza era 0 dBm, che era 0,775 V, quindi calibravi i tuoi misuratori di livello così. Il problema è sorto perché, una volta che un misuratore di livello che misura la tensione è calibrato in questo modo, leggerà 0 dBm a 0,775 V anche se non è collegato a 600 Ω Quindi, forse illogicamente, dBm significherà a volte dB rispetto a 0,775 V. (Quando ero un ragazzo, le calcolatrici erano costose così usavo il vecchio regolo calcolatore di papà, che aveva il fattore 0,775 segnato sulla finestra del cursore per facilitare tali calcoli).

Come convertire dBV o dBm in dB di livello sonoro? Non c’è un modo semplice. Dipende da come si converte la potenza elettrica in potenza sonora. Anche se il segnale elettrico è collegato direttamente a un altoparlante, la conversione dipenderà dall’efficienza e dall’impedenza dell’altoparlante. E naturalmente ci può essere un amplificatore di potenza, e varie complicazioni acustiche tra il punto in cui misurate i dBV sul banco di missaggio e il punto in cui le vostre orecchie sono nel campo sonoro.

Intensità, radiazione e dB

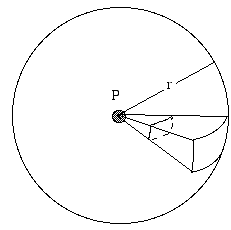
Come dipende il livello del suono (o il livello del segnale radio, ecc.) dalla distanza dalla sorgente?

Una sorgente che emette radiazioni allo stesso modo in tutte le direzioni è detta isotropa. Consideriamo una sorgente sonora isolata, lontana da qualsiasi superficie riflettente – forse un uccello che canta in alto nell’aria. Immagina una sfera di raggio r, centrata sulla sorgente. La sorgente emette una potenza totale P, continuamente. Questa potenza sonora si diffonde e passa attraverso la superficie della sfera. Se la sorgente è isotropa, l’intensità I è la stessa ovunque su questa superficie, per definizione. L’intensità I è definita come la potenza per unità di superficie. La superficie della sfera è 4πr2, quindi la potenza (nel nostro esempio, la potenza sonora) che passa attraverso ogni metro quadrato di superficie è, per definizione:

I = P/4πr2.

Quindi vediamo che, per una sorgente isotropa, l’intensità è inversamente proporzionale al quadrato della distanza dalla sorgente:

I2/I1 = r12/r22.

Ma l’intensità è proporzionale al quadrato della pressione sonora, quindi potremmo ugualmente scrivere:

p2/p1 = r1/r2.

Quindi, se raddoppiamo la distanza, riduciamo la pressione sonora di un fattore 2 e l’intensità di un fattore 4: in altre parole, riduciamo il livello sonoro di 6 dB. Se aumentiamo r di un fattore 10, diminuiamo il livello di 20 dB, ecc.

Attenzione, però, che molte sorgenti non sono isotrope, specialmente se la lunghezza d’onda è più piccola o di dimensioni paragonabili alla sorgente. Inoltre, le riflessioni sono spesso abbastanza importanti, soprattutto se il terreno è vicino, o se siete al chiuso.

Pressione, intensità e impedenza specifica

Per le onde acustiche, l’impedenza acustica specifica z è definita come il rapporto tra la pressione acustica p e la velocità media delle particelle u, dovuta al suono ave, z = p/u . In Impedenza acustica, intensità e potenza, mostriamo come mettere in relazione la pressione acustica RMS p e l’intensità I:
I = p2/z

Per l’aria, l’impedenza acustica specifica z è 420 kg.s-1.m-2 = 420 Pa.s.m-1. Per l’acqua (dolce), l’impedenza acustica specifica dell’acqua è 1,48 MPa.s.m-1. Quindi un’onda sonora in acqua con la stessa pressione ha un’intensità molto più bassa di una in aria.

dBi e la radiazione che varia con la direzione

La radiazione che varia nella direzione è chiamata anisotropa. Per molti casi nella comunicazione, la radiazione isotropa è sprecata: perché emettere una frazione sostanziale di potenza verso l’alto se il ricevitore è, come te, relativamente vicino al livello del suolo. Per i suoni di breve lunghezza d’onda (compresa la maggior parte della gamma importante per il discorso), un megafono può aiutare a rendere la voce più anisotropa. Per la radio, una vasta gamma di design permette alle antenne di essere altamente anisotrope sia per la trasmissione che per la ricezione.

Quindi, quando si è interessati all’emissione in (o alla ricezione da) una particolare direzione, si vuole che il rapporto di intensità misurato in quella direzione, a una data distanza, sia più alto di quello misurato alla stessa distanza da un radiatore isotropo (o ricevuto da un ricevitore isotropo). Questo rapporto è chiamato guadagno; esprimete il rapporto in dB e avrete il guadagno in dBi per quel radiatore. Questa unità è usata principalmente per le antenne, sia in trasmissione che in ricezione, ma a volte è usata per le sorgenti sonore e i microfoni direzionali.

Problemi di esempio

Alcune persone hanno scritto chiedendo esempi di utilizzo dei dB nei calcoli. Quindi…
• A parità di condizioni, quanto è più forte l’altoparlante pilotato (nella sua gamma lineare) da un amplificatore da 100 W rispetto a un amplificatore da 10 W?

  Le potenze differiscono di un fattore dieci, che, come abbiamo visto sopra, è 10 dB. A parità di condizioni qui significa che le risposte in frequenza sono uguali e che si usa lo stesso segnale d’ingresso, ecc. Quindi la dipendenza dalla frequenza dovrebbe essere la stessa. 10 dB corrispondono a 10 phon. Per ottenere un raddoppio del volume percepito, è necessario un aumento di 10 phon. Quindi l’altoparlante pilotato dall’amplificatore da 100 W è due volte più forte di quello pilotato da 10 W, supponendo di rimanere nella gamma lineare e di non distorcere o distruggere l’altoparlante. (L’amplificatore da 100 W produce il doppio dei soni rispetto a quello da 10 W.)

• Sono a una distanza R da una piccola fonte di suono (di dimensioni molto inferiori a R), a livello del suolo all’aperto dove le riflessioni possono essere trascurate. Il livello sonoro è L. Se ora mi sposto a una distanza nR (n è un numero, e nR è ancora molto maggiore della dimensione della sorgente), quale sarà il nuovo livello sonoro?

  Prima di tutto, notate che la trascuratezza delle riflessioni è molto importante. Questo calcolo non funzionerà all’interno di una stanza, dove le riflessioni dal muro (che producono collettivamente la riverberazione) rendono il calcolo abbastanza difficile. All’aperto, l’intensità sonora è proporzionale a 1/r2, dove r è la distanza dalla sorgente. (La costante di proporzionalità dipende da quanto bene il terreno riflette, e non ci riguarda qui, perché si annullerà approssimativamente nel calcolo, purché r sia ragionevolmente grande). Quindi, se aumentiamo r da R a nR, diminuiamo l’intensità da I a I/n 2.

  La differenza in decibel tra i due segnali di intensità I 2 e I 1 è definita sopra come

  ΔL = 10 log (I2/I1) = 10 log ((I/n 2)/I) = 10 log (1/n 2) = -10 log (n 2) = -20 log n.

  Per esempio, se n è 2 (cioè se andiamo al doppio della distanza), l’intensità si riduce di un fattore quattro e il livello sonoro scende da L a (L – 6dB).

• Se, in condizioni ideali di quiete, un giovane può sentire un tono di 1 kHz a 0 dB emesso da un altoparlante (forse un softspeaker?), di quanto deve essere aumentata la potenza dell’altoparlante per portare il suono a 110 dB (un livello pericolosamente alto ma sopravvivibile)?

  La differenza in decibel tra i due segnali di potenza P2 e P1 è definita sopra come

  ΔL = 10 log (P2/P1) dB quindi, elevando 10 alla potenza di queste due quantità uguali:
  10L/10 = P2/P1 quindi:
  P2/P1 = 10110/10 = 1011 = centomila milioni.

  che è una dimostrazione che l’orecchio umano ha una gamma dinamica notevolmente grande, forse maggiore di quella dell’occhio.

• Un amplificatore ha un ingresso di 10 mV e un’uscita di 2 V. Qual è il suo guadagno di tensione in dB?

  La tensione, come la pressione, appare al quadrato nelle espressioni di potenza o intensità. (La potenza dissipata in una resistenza R è V2/R.) Quindi, per convenzione, definiamo:

  guadagno = 20 log (Vout/Vin)
  = 20 log (2V/10mV)
  = 46 dB

  (Nei casi acustici dati sopra, abbiamo visto che il rapporto di pressione, espresso in dB, era lo stesso del rapporto di potenza: questa era la ragione del fattore 20 nella definizione dei dB per la pressione. Vale la pena notare che, nell’esempio del guadagno di tensione, è improbabile che il guadagno di potenza dell’amplificatore sia uguale al guadagno di tensione, che è definito dalla convenzione usata qui. La potenza è proporzionale al quadrato della tensione in una data resistenza. Tuttavia, le impedenze di ingresso e di uscita degli amplificatori sono spesso molto diverse. Per esempio, un amplificatore a buffer o un inseguitore di emettitore ha un guadagno di tensione di circa 1, ma un grande guadagno di corrente).

• Qual è la differenza, in dB, tra l’irraggiamento (intensità luminosa) sulla terra (8,3 minuti luce dal sole) e su Urano (160 minuti luce)?

  Come il suono, l’intensità luminosa isotropa diminuisce come r-2, quindi il rapporto di intensità è (160/8.3)2 = 20 log (160/8.3) = 26 dB.

Salute e sicurezza sul lavoro

Diversi paesi e province hanno ovviamente diverse leggi sull’esposizione al rumore sul lavoro, che sono applicate con diverso entusiasmo. Molti di questi regolamenti hanno un limite per l’esposizione al rumore continuo di 85 dB(A), per un turno di 8 ore. Per ogni aumento di 3 dB, l’esposizione permessa è dimezzata. Così, se si lavora in un locale notturno dove la musica amplificata produce 100 dB(A) vicino alle orecchie, l’esposizione permessa è di 15 minuti. C’è un limite per il rumore impulsivo come le armi da fuoco o gli strumenti che usano colpi esplosivi. (Ci sono molti documenti che forniscono consigli su come ridurre l’esposizione al rumore alla fonte (cioè abbassare il livello della musica), tra la fonte e l’orecchio (cioè allontanarsi dagli altoparlanti di un concerto) e all’orecchio (cioè indossare tappi o protezioni acustiche industriali). La gestione del rumore e la protezione dell’udito sul lavoro è il codice di pratica nello stato del New South Wales, Australia (indirizzo dell’autore).

Alcune FAQ

• Quanto rumore fa un aereo? Un treno? Una persona che canta? Un cane che abbaia? Un utensile elettrico? Le risposte a questa domanda variano considerevolmente. Dipende fortemente da quanto si è lontani, se si è al chiuso o no, se c’è riverbero, quanto è forte la sorgente particolare e qual è il suo spettro. Dare dei valori, senza essere molto specifici sulle condizioni, sarebbe in qualche modo fuorviante. Poiché il resto di questa pagina vuole essere affidabile, per quanto va, preferisco non dare valori qui.
• Come si fa ad “aggiungere decibel”, cioè quale livello sonoro si ottiene quando si aggiunge il livello a al livello b? Se le fonti sono coerenti (il che di solito significa che alla fine provengono dalla stessa fonte), allora ci possono essere complicati effetti di interferenza. Nella maggior parte dei casi, dove le fonti sono indipendenti, si possono sommare le intensità e poi convertire in decibel. Tuttavia, se vi vengono dati i livelli sonori in dB(A), non è così facile tornare all’intensità, e bisogna sapere qualcosa sullo spettro del suono. Se si conosce la distribuzione del suono in diverse bande di frequenza, si può usare l’applet a questo link.
• Some of the questions on our FAQ in music acoustics relate to decibels, including
  • Why do the sounds of two musical instruments always reinforce, and never cancel out?
  • How much does one more violin add to the sound level of a section of n violins?
  • Does adding two equal sounds give an increase of 3 or 6 dB? Why?
  • What is the loudest sound?
  • Is there really no sound in space?

Related pages

• Measure your own hearing response
• Adding sound levels from incoherent sources
• What are interference beats and Tartini tones?
• FAQ in music acoustics
• Loudness and spectra: how spectral content and other features are related to loudness
• Formants: what are they? A discussion of the different meanings of this term
• Music acoustics home page
• Physclips: a multi-level, multimedia introduction to mechanics.
• A list of other educational web sites from this author.