Distribuzione marginale

Distribuzioni di probabilità > Distribuzione marginale

Cos’è una distribuzione marginale?

Guarda il video o leggi l’articolo qui sotto:

La definizione tecnica può essere un po’ noiosa da guardare:

Definizione di una distribuzione marginale = Se X e Y sono variabili casuali discrete e f (x,y) è il valore della
loro distribuzione di probabilità comune a (x,y), le funzioni date da:
g(x) = Σy f (x,y) e h(y) = Σx f (x,y) sono le distribuzioni marginali di X e Y, rispettivamente.

Se sei bravo con le equazioni, questo è probabilmente tutto quello che devi sapere. Vi dice come trovare una distribuzione marginale. Ma se questa formula vi fa venire il mal di testa (cosa che succede alla maggior parte delle persone!), potete usare una tabella di distribuzione di frequenza per trovare una distribuzione marginale.

Una distribuzione marginale prende il suo nome perché appare ai margini di una tabella di distribuzione di probabilità.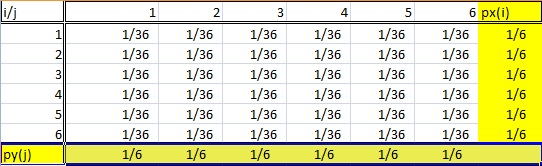

Naturalmente, non è così semplice. Non si può semplicemente guardare una qualsiasi tabella di distribuzione di frequenza e dire che l’ultima colonna (o riga) è una “distribuzione marginale”. Le distribuzioni marginali seguono un paio di regole:

• La distribuzione deve essere da dati bivariati. Bivariata è solo un altro modo di dire “due variabili”, come X e Y. Nella tabella sopra, le variabili casuali i e j provengono dal lancio di due dadi.
• Una distribuzione marginale è quella in cui si è interessati solo ad una delle variabili casuali. In altre parole, o X o Y. Se guardate la tabella delle probabilità qui sopra, le probabilità di somma di una variabile sono elencate nella riga inferiore e le altre probabilità di somma sono elencate nella colonna di destra. Quindi questa tabella ha due distribuzioni marginali.

Differenza tra distribuzione marginale e distribuzione condizionata.

Una distribuzione condizionata è quella in cui siamo interessati solo a una particolare sottopopolazione del nostro intero set di dati. Nell’esempio del lancio dei dadi, questo potrebbe essere “lanciare un due” o “lanciare un sei”. L’immagine qui sotto mostra due sottopopolazioni evidenziate (e quindi due distribuzioni condizionali).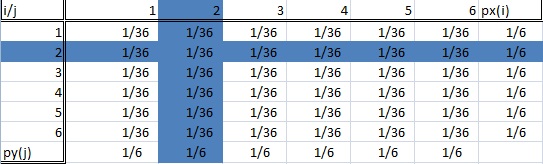

Come calcolare la probabilità della distribuzione marginale

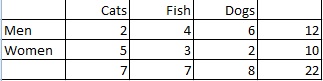
Domanda di esempio: Calcolare la distribuzione marginale delle preferenze degli animali domestici tra uomini e donne:
Soluzione:
Passo 1: Contare il numero totale di persone. In questo caso il totale è dato nella colonna di destra (22 persone).
Passo 2: Conta il numero di persone che preferiscono ogni tipo di animale domestico e poi trasforma il rapporto in una probabilità:
Persone che preferiscono i gatti: 7/22 = .32
Persone che preferiscono i pesci: 7/22 = .32
Persone che preferiscono i cani: 8/22 = .36
Suggerimento: Puoi controllare la tua risposta assicurandoti che le probabilità siano tutte pari a 1.

Domanda di esempio 2 (Eventi mutualmente esclusivi): Se P(A) = 0.20, P(b) = 0.70, ed entrambi gli eventi si escludono a vicenda, trova P(B’∩A), P(B’∩A’) e P(B∩A’).
Se non hai familiarità con questa notazione, P(A’) significa “non A”, o il complemento. P(B’∩A) significa “l’intersezione di non B e A”).

Risposta:
Si potrebbero calcolare le probabilità individualmente, ma sono molto più facili da capire usando una tabella.

Step 1: Compilare una tabella di frequenza con le informazioni date. La probabilità totale deve essere uguale a 1, quindi puoi aggiungere anche questo ai margini (totali). La semplice addizione/algebra riempie gli spazi vuoti dei margini. Per esempio, sulla riga inferiore 0.70 + x = 1.00 quindi Il totale marginale per B’ deve essere 0.30.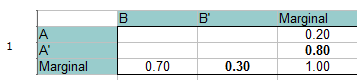

Step 2: Aggiungere 0 per l’intersezione di A e B, in alto a sinistra della tabella. Puoi farlo perché A e B si escludono a vicenda e non possono accadere insieme.

Step 3: Riempi il resto degli spazi vuoti usando la semplice addizione/algebra.

Leggere dalla tabella (guardare le intersezioni delle due probabilità dichiarate):
P(B’∩A) = 0,20
P(B’∩A’) = 0,10
P(B∩A’) = 0,70.

Esempio domanda 3 (Eventi indipendenti): Se P(A) = 0,20, P(b) = 0,70, ed entrambi gli eventi sono indipendenti, trovare P(B’∩A), P(B’∩A’) e P(B∩A’).

Risposta: Questa volta, A e B sono indipendenti, quindi la probabilità che accadano entrambi nello stesso momento è 0,14 (P(A)*P(B) = 0,20 * 0,70 = 0,14). Questo valore va in alto a sinistra (intersezione di A e B). Compilate il resto della tabella esattamente come nei passi precedenti.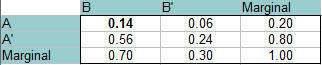

Leggete le risposte dalla tabella (dalle intersezioni delle due probabilità):
P(B’∩A): 0.06
P(B’∩A’): 0.24
P(B∩A’): 0.56.

Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, pp. 536 e 571, 2002.
Agresti A. (1990) Analisi dei Dati Categorici. John Wiley and Sons, New York.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education

——————————————————————————

Hai bisogno di aiuto per un compito a casa o per un test? Con Chegg Study, puoi ottenere soluzioni passo dopo passo alle tue domande da un esperto del settore. I tuoi primi 30 minuti con un tutor Chegg sono gratuiti!