Solving the Königsberg Bridge Problem

This proof is accessible to ANYONE — no mathematics knowledge required! (perfect for if you are a bit bored and in isolation, like me right now!)

The Königsberg bridge problem shows the beauty of mathematics to transform the impossible to the obvious. It also gives an insight into the mind of the genius Leonhard Euler.

Stating the problem

Have a look at the map above.

It’s a diagram of the rivers and bridges of Königsberg. The areas A, B, C and D are bits of land, joined by the bridges, but otherwise cut off from each other by water.

A map of the city is below. Puoi guardare entrambi i diagrammi – entrambi catturano le informazioni chiave: quali porzioni di terra sono collegate a quali altre porzioni di terra, e da quanti ponti.

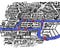
In termini tecnici, lo stiamo rappresentando come un grafico. Le chiazze di terra sono i vertici, e i ponti sono i bordi. Ma questo non è importante.

Il problema è se è possibile trovare un percorso che passi esattamente una volta per ogni ponte. Ciò significa che, nella nostra passeggiata per la città, vogliamo che il nostro percorso passi su ogni ponte, ma non può passarci sopra due volte, o tre volte… In pratica, se ci si ritrova sullo stesso ponte di prima, il percorso non è valido. Se finisci la tua passeggiata e c’è un ponte che non hai attraversato, allora il tuo percorso non era valido.

La soluzione

Considera ogni blob di terra. Ogni ponte è collegato a due blob di terra (è così che funzionano i ponti). Si dà il caso che ogni blob di terra abbia un numero dispari di ponti collegati.

Ora, consideriamo come sarebbe una passeggiata valida.

Percorrendo la tua passeggiata, registra su un blocco note ogni volta che sei in un certo blob di terra. Per esempio, se cominci dall’estremità più a sud della città, ne prendi nota (fai una foto, compra un souvenir…) e se ti ritrovi lì, aumenti a due il conteggio per il settore sud.

Per ogni blob di terra ci sono due casi

(1) questo è un settore della città in cui non iniziamo la nostra passeggiata, né vi finiamo la nostra passeggiata

(2) questo è un settore della città in cui o iniziamo la nostra passeggiata, o vi finiamo la nostra passeggiata, o entrambi.

Chiaramente, ci sono al massimo 2 settori della città del secondo tipo. Non possiamo iniziare in due posti contemporaneamente, né possiamo finire in due posti contemporaneamente.

Poiché ci sono quattro sezioni della città, ciò significa che ci sono almeno due sezioni della città, nella nostra passeggiata, in cui non finiamo né iniziamo. Scegliamo uno di essi.

Ogni volta che entriamo in quel settore, usiamo un ponte, e ogni volta che ne usciamo ne usiamo un altro. Ma ogni settore ha un numero dispari di ponti collegati ad esso! Questa è una contraddizione. Per capire perché, ricordiamo che ogni settore ha o 3 ponti, o ha 5 ponti attaccati.

Se siamo nel settore una volta, possiamo usare solo due dei suoi ponti. Se ci entriamo due volte, useremmo quattro dei suoi ponti (o finiremmo i ponti, se ne avesse solo tre). Se ci entriamo tre volte, avremmo bisogno di 6 ponti, che non possiamo avere. Quindi il requisito di entrare e uscire da un settore della città che non è il nostro punto di partenza o di arrivo contraddice il fatto che il numero di ponti di collegamento è dispari per ogni settore.