Tipi di interpolazione – Vantaggi e svantaggi
Metodi di interpolazione
L’interpolazione è il processo di utilizzo di punti con valori noti o punti campione per stimare valori in altri punti sconosciuti. Può essere usato per predire valori sconosciuti per qualsiasi dato puntuale geografico, come elevazione, precipitazioni, concentrazioni chimiche, livelli di rumore, e così via.
I metodi di interpolazione disponibili sono elencati di seguito.
Inverse Distance Weighted (IDW)
L’interpolatore Inverse Distance Weighting assume che ogni punto di input abbia una influenza locale che diminuisce con la distanza. Pesa i punti più vicini alla cella di elaborazione più di quelli più lontani. Un numero specificato di punti, o tutti i punti entro un raggio specificato possono essere usati per determinare il valore di uscita di ogni località. L’uso di questo metodo presuppone che la variabile da mappare diminuisca di influenza con la distanza dalla sua posizione campionata.
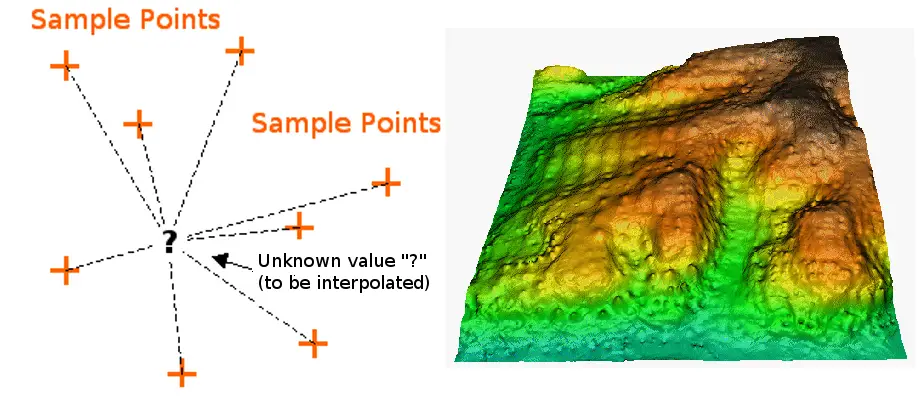
Interpolazione IDW; Per gentile concessione: QGIS
L’algoritmo Inverse Distance Weighting (IDW) è effettivamente un interpolatore a media mobile che viene solitamente applicato a dati altamente variabili. Per alcuni tipi di dati è possibile tornare al sito di raccolta e registrare un nuovo valore che è statisticamente diverso dalla lettura originale ma all’interno della tendenza generale per l’area.
La superficie interpolata, stimata con una tecnica di media mobile, è inferiore al valore massimo locale e superiore al valore minimo locale.

Superficie interpolata IDW; Cortesia:ESRI
L’interpolazione IDW implementa esplicitamente il presupposto che le cose vicine sono più simili di quelle lontane. Per predire un valore per qualsiasi posizione non misurata, IDW userà i valori misurati che circondano la posizione di predizione. I valori misurati più vicini alla posizione di predizione avranno più influenza sul valore previsto rispetto a quelli più lontani. Quindi, IDW assume che ogni punto misurato abbia un’influenza locale che diminuisce con la distanza. La funzione IDW dovrebbe essere usata quando l’insieme dei punti è abbastanza denso da catturare l’estensione della variazione locale della superficie necessaria per l’analisi. IDW determina i valori delle celle usando una combinazione di punti campione con ponderazione lineare. Pesa i punti più vicini alla posizione di predizione più di quelli più lontani, da qui il nome di distanza inversa ponderata.
La tecnica IDW calcola un valore per ogni nodo della griglia esaminando i punti dati circostanti che si trovano entro un raggio di ricerca definito dall’utente. Alcuni o tutti i punti di dati possono essere usati nel processo di interpolazione. Il valore del nodo è calcolato facendo la media della somma ponderata di tutti i punti. I punti dati che si trovano progressivamente più lontani dal nodo influenzano il valore calcolato molto meno di quelli che si trovano più vicini al nodo.
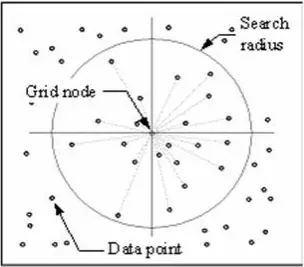
Viene generato un raggio attorno ad ogni nodo della griglia da cui vengono selezionati i punti dati da utilizzare nel calcolo. Options to control the use of IDW include power, search radius, fixed search radius, variable search radius and barrier.
Note: The optimal power (p) value is determined by minimizing the root mean square prediction error (RMSPE).
Advantages
- Can estimate extreme changes in terrain such as: Cliffs, Fault Lines.
- Dense evenly space points are well interpolated (flat areas with cliffs).
- Can increase or decrease amount of sample points to influence cell values.
Disadvantages
- Cannot estimate above maximum or below minimum values.
- Not very good for peaks or mountainous areas.
Natural Neighbour Inverse Distance Weighted (NNIDW)
Natural neighbor interpolation has many positive features, can be used for both interpolation and extrapolation, and generally works well with clustered scatter points. Un altro metodo di media ponderata, l’equazione di base usata nell’interpolazione dei vicini naturali è identica a quella usata nell’interpolazione IDW. Questo metodo può gestire in modo efficiente grandi insiemi di dati di punti di input. Quando si usa il metodo Natural Neighbor, le coordinate locali definiscono la quantità di influenza che ogni punto di dispersione avrà sulle celle di output.
Il metodo Natural Neighbour è una tecnica di stima geometrica che utilizza regioni di vicinato naturale generate intorno a ogni punto del set di dati.
Come IDW, questo metodo di interpolazione è un metodo di interpolazione a media pesata. Tuttavia, invece di trovare il valore di un punto interpolato usando tutti i punti di input ponderati per la loro distanza, l’interpolazione Natural Neighbors crea una triangolazione di Delauney dei punti di input e seleziona i nodi più vicini che formano un guscio convesso intorno al punto di interpolazione, quindi pondera i loro valori per area proporzionale. Questo metodo è più appropriato quando i punti dei dati campione sono distribuiti con densità non uniforme. È una buona tecnica di interpolazione generale e ha il vantaggio di non dover specificare parametri come raggio, numero di vicini o pesi.

IDW naturale: Per gentile concessione: ESRI
Questa tecnica è progettata per onorare i valori minimi e massimi locali nel file di punti e può essere impostata per limitare i superamenti dei valori alti locali e i superamenti dei valori bassi locali. Il metodo permette quindi la creazione di modelli di superficie accurati da set di dati che sono molto scarsamente distribuiti o molto lineari nella distribuzione spaziale.
Avantaggi
- Gestisce un gran numero di punti campione in modo efficiente.
Spline
La Spline stima i valori usando una funzione matematica che minimizza la curvatura complessiva della superficie, ottenendo una superficie liscia che passa esattamente attraverso i punti di input.

Spline: Per gentile concessione: ESRI
Concettualmente, è analogo al piegare un foglio di gomma per passare attraverso punti noti, minimizzando la curvatura totale della superficie. Si adatta una funzione matematica a un numero specificato di punti di ingresso più vicini mentre passa attraverso i punti campione. Questo metodo è il migliore per superfici che variano dolcemente, come l’elevazione, l’altezza delle falde acquifere o le concentrazioni di inquinamento.
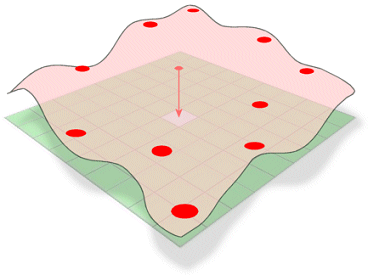
Ci sono due metodi spline: regolarizzato e tensionale.
Un metodo regolarizzato crea una superficie liscia, che cambia gradualmente, con valori che possono trovarsi al di fuori dell’intervallo dei dati campione. Incorpora la prima derivata (pendenza), la seconda derivata (tasso di variazione della pendenza) e la terza derivata (tasso di variazione della seconda derivata) nei suoi calcoli di minimizzazione.
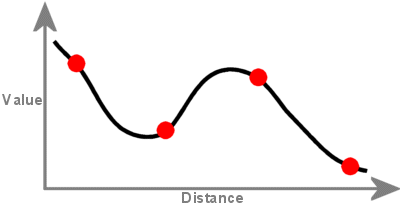
Una superficie creata con interpolazione Spline passa attraverso ogni punto campione e può superare l’intervallo di valori del set di punti campione.
Anche se una Spline di tensione usa solo le derivate prime e seconde, include più punti nei calcoli della Spline, che di solito crea superfici più lisce ma aumenta il tempo di calcolo.
Questo metodo tira una superficie sui punti acquisiti ottenendo un effetto allungato. Spline usa linee curve (metodo Linee curvilinee) per calcolare i valori delle celle.
Scegliere un peso per le interpolazioni Spline
Spline regolarizzata: Più alto è il peso, più liscia è la superficie. I pesi tra 0 e 5 sono adatti. I valori tipici sono 0, .001, .01, .1,e .5.
Splinea di tensione: Più alto è il peso, più grossolana è la superficie e più i valori sono conformi alla gamma dei dati del campione. I valori del peso devono essere maggiori o uguali a zero. Typical values are 0, 1, 5, and 10.
Advantages
- Useful for estimating above maximum and below minimum points.
- Creates a smooth surface effect.
Disadvantages
- Cliffs and fault lines are not well presented because of the smoothing effect.
- When the sample points are close together and have extreme differences in value, Spline interpolation doesn’t work as well. This is because Spline uses slope calculations (change over distance) to figure out the shape of the flexible rubber sheet.
Kriging
Kriging is a geostatistical interpolation technique that considers both the distance and the degree of variation between known data points when estimating values in unknown areas. A kriged estimate is a weighted linear combination of the known sample values around the point to be estimated.
Procedura di kriging che genera una superficie stimata da un insieme sparso di punti con valori z. Il Kriging presuppone che la distanza o la direzione tra i punti campione rifletta una correlazione spaziale che può essere utilizzata per spiegare la variazione della superficie. Lo strumento Kriging adatta una funzione matematica a un numero specificato di punti, o a tutti i punti entro un raggio specificato, per determinare il valore di uscita per ogni posizione. Il Kriging è un processo a più fasi; include l’analisi statistica esplorativa dei dati, la modellazione del variogramma, la creazione della superficie e (opzionalmente) l’esplorazione di una superficie di varianza. Il kriging è più appropriato quando si sa che c’è una distanza spazialmente correlata o un bias direzionale nei dati. È spesso usato nella scienza del suolo e nella geologia.
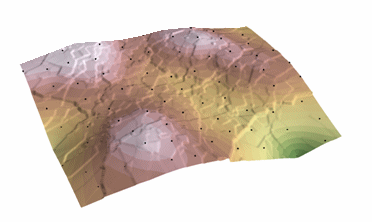
Kriging: Courtesy: ESRI
The predicted values are derived from the measure of relationship in samples using sophisticated weighted average technique. It uses a search radius that can be fixed or variable. The generated cell values can exceed value range of samples, and the surface does not pass through samples.
The Kriging Formula
Kriging is similar to IDW in that it weights the surrounding measured values to derive a prediction for an unmeasured location. The general formula for both interpolators is formed as a weighted sum of the data:
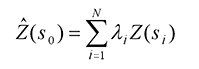
- where:
Z(si) = the measured value at the ith location
λi = an unknown weight for the measured value at the ith location
s0 = the prediction location
N = the number of measured values
In IDW, the weight, λi, depends solely on the distance to the prediction location. Tuttavia, con il metodo kriging, i pesi si basano non solo sulla distanza tra i punti misurati e la località di predizione, ma anche sulla disposizione spaziale complessiva dei punti misurati. Per utilizzare la disposizione spaziale nei pesi, l’autocorrelazione spaziale deve essere quantificata. Così, nel kriging ordinario, il peso, λi, dipende da un modello adattato ai punti misurati, dalla distanza dalla località di predizione e dalle relazioni spaziali tra i valori misurati intorno alla località di predizione. Le sezioni seguenti discutono come la formula generale del kriging viene usata per creare una mappa della superficie di predizione e una mappa dell’accuratezza delle predizioni.
Tipi di Kriging
Kriging ordinario
Il kriging ordinario assume il modello
Z(s) = µ + ε(s),
dove µ è una costante sconosciuta. Uno dei problemi principali riguardanti il kriging ordinario è se l’assunzione di una media costante sia ragionevole. Sometimes there are good scientific reasons to reject this assumption. However, as a simple prediction method, it has remarkable flexibility.
Ordinary kriging can use either semivariograms or covariances, use transformations and remove trends, and allow for measurement error.
Simple Kriging
Simple kriging assumes the model
Z(s) = µ + ε(s),
where µ is a known constant.
Simple kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Universal Kriging
Universal kriging assumes the model
Z(s) = µ(s) + ε(s),
where µ(s) is some deterministic function.
Universal kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Indicator Kriging
Indicator kriging assume il modello
I(s) = µ + ε(s),
dove µ è una costante sconosciuta e I(s) è una variabile binaria. La creazione di dati binari può essere attraverso l’uso di una soglia per i dati continui, o può essere che i dati osservati siano 0 o 1. Per esempio, si potrebbe avere un campione che consiste in informazioni sul fatto che un punto sia o meno un habitat forestale o non forestale, dove la variabile binaria indica l’appartenenza alla classe. Usando variabili binarie, il kriging indicatore procede come il kriging ordinario.
Il kriging indicatore può usare sia semivariogrammi che covarianze.
Kriging delle probabilità
Il kriging delle probabilità assume il modello
I(s) = I(Z(s) > ct) = µ1 + ε1(s)Z(s) = µ2 + ε2(s),
dove µ1 e µ2 sono costanti sconosciute e I(s) è una variabile binaria creata utilizzando un indicatore di soglia, I(Z(s) > ct). Si noti che ora ci sono due tipi di errori casuali, ε1(s) e ε2(s), quindi c’è autocorrelazione per ciascuno di essi e correlazione incrociata tra loro. Il kriging delle probabilità cerca di fare la stessa cosa del kriging degli indicatori, ma usa il cokriging nel tentativo di fare un lavoro migliore.
Il kriging probabilistico può usare sia semivariogrammi che covarianze, cross-covarianze e trasformazioni, ma non può tenere conto degli errori di misura.
style=”display:inline-block;width:468px;height:60px” data-ad-client=”ca-pub-7134201556760050″ data-ad-slot=”9271753327″>
Kriging disgiuntivo
Il kriging disgiuntivo assume il modello
f(Z(s)) = µ1 + ε(s),
dove µ1 è una costante sconosciuta e f(Z(s)) è una funzione arbitraria di Z(s). Si noti che si può scrivere f(Z(s)) = I(Z(s) > ct), quindi il kriging indicatore è un caso speciale del kriging disgiuntivo. In Geostatistical Analyst, è possibile prevedere sia il valore stesso che un indicatore con il kriging disgiuntivo.
In generale, il kriging disgiuntivo cerca di fare di più del kriging ordinario. Mentre le ricompense possono essere maggiori, lo sono anche i costi. Disjunctive kriging requires the bivariate normality assumption and approximations to the functions fi(Z(si)); the assumptions are difficult to verify, and the solutions are mathematically and computationally complicated.
Disjunctive kriging can use either semivariograms or covariances and transformations, but it cannot allow for measurement error.
Advantages
- Directional influences can be accounted for: Soil Erosion, Siltation Flow, Lava Flow and Winds.
- Exceeds the minimum and maximum point values
Disadvantages
- Does not pass through any of the point values and causes interpolated values to be higher or lower then real values.
** Per avere una visione approfondita dell’approccio matematico al Kriging si prega di cliccare su Kriging un metodo di interpolazione.
PointInterp
Un metodo simile all’IDW, la funzione PointInterp permette un maggiore controllo sul quartiere di campionamento. L’influenza di un particolare campione sul valore della cella della griglia interpolata dipende dal fatto che il punto campione si trovi o meno nel quartiere della cella e da quanto lontano dalla cella da interpolare si trova. I punti fuori dal quartiere non hanno alcuna influenza.

PointInterp; Cortesia: ESRI
Il valore ponderato dei punti all’interno del quartiere è calcolato utilizzando un’interpolazione ponderata a distanza inversa o interpolazione a distanza esponenziale inversa. Questo metodo interpola un raster usando le caratteristiche dei punti, ma permette diversi tipi di vicinato. I quartieri possono avere forme come cerchi, rettangoli, poligoni irregolari, anelli o cunei.
Trend
Trend è un metodo statistico che trova la superficie che si adatta ai punti campione usando una regressione ai minimi quadrati. Si adatta un’equazione polinomiale all’intera superficie. Questo risulta in una superficie che minimizza la varianza della superficie in relazione ai valori di input. La superficie è costruita in modo che per ogni punto di ingresso, il totale delle differenze tra i valori reali e i valori stimati (cioè la varianza) sarà il più piccolo possibile.

Trend; Courtsey:ESRI
È un interpolatore inesatto, e la superficie risultante raramente passa attraverso i punti di input. Tuttavia, questo metodo rileva le tendenze nei dati campione ed è simile ai fenomeni naturali che tipicamente variano in modo uniforme.
Vantaggi
- Le superfici di tendenza sono buone per identificare modelli su scala grossolana nei dati; la superficie interpolata raramente passa attraverso i punti campione.
Topo to Raster
Interpolando i valori di elevazione per un raster, il metodo Topo to Raster impone dei vincoli che assicurano un modello digitale di elevazione idrologicamente corretto che contiene una struttura di drenaggio collegata e rappresenta correttamente le creste e i corsi d’acqua dai dati di contorno di input. Utilizza una tecnica di interpolazione iterativa a differenza finita che ottimizza l’efficienza computazionale dell’interpolazione locale senza perdere la continuità superficiale dell’interpolazione globale. È stato specificamente progettato per lavorare in modo intelligente con input di contorno.
Di seguito è riportato un esempio di superficie interpolata da punti di quota, curve di livello, linee di flusso e poligoni di lago utilizzando l’interpolazione Topo to Raster.
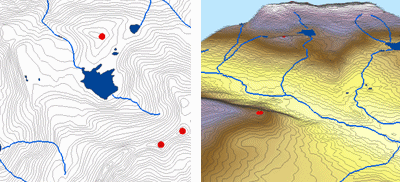
Topo in raster; Per gentile concessione: ESRI
Topo to Raster è uno strumento specializzato per creare superfici raster idrologicamente corrette da dati vettoriali di componenti del terreno come punti di elevazione, curve di livello, linee di flusso, poligoni di laghi, punti di caduta e poligoni di confine dell’area di studio.
Densità
Gli strumenti di densità (disponibili in ArcGIS) producono una superficie che rappresenta quanto o quanti elementi ci sono per unità di superficie. Lo strumento densità è utile per creare superfici di densità per rappresentare la distribuzione di una popolazione di animali selvatici da un insieme di osservazioni, o il grado di urbanizzazione di un’area in base alla densità delle strade.

Density Raster; Courtest: ERSI
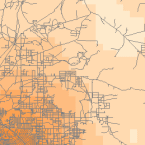
Density and Roads; Courtesy: ESRI
There are density tools for point and line features in ArcGIS.
Related Topics
- What is Interpolation ?
- Classification of Interpolation Techniques.
- Choosing the Right Interpolation Method