カーネルトリックとは何ですか?
機械学習でカーネルについて話すとき、最初に思い浮かぶのはサポート ベクトル マシン (SVM) モデルでしょう。
カーネルとは何か、なぜそれが重要なのかを理解していただくために、まず SVM モデルの基本を紹介します。
SVM モデルは教師あり機械学習モデルで、主に分類に使用されます (ただし回帰にも使用できます!)。 決定境界を形成することによって、異なるグループを分離する方法を学習します。

上のグラフで、観測のクラスは2つあると気付きました。 青いポイントと紫のポイントです。 左のグラフに示すように、これらの 2 つのクラスを分離する方法はたくさんあります。 しかし、我々は、この2つのクラス間のマージンを最大化できる「最良の」超平面を見つけたいのです。これは、超平面と両側の最も近いデータ点との間の距離が最大であることを意味します。 新しいデータ点が超平面のどちらの側に位置するかによって、新しい観測にクラスを割り当てることができます。
上記の例では、単純に聞こえます。 しかし、すべてのデータが直線的に分離可能なわけではありません。 実際、現実の世界では、ほとんどすべてのデータはランダムに分布しており、異なるクラスを線形に分離することは困難です。

なぜカーネル トリックを使うことは重要か

上の図にあるように、データを 2 次元空間から 3 次元空間にマッピングする方法を見つけると、異なるクラスを明確に分割する決定面を見つけることができるようになります。 このデータ変換プロセスで私が最初に考えたのは、すべてのデータ点をより高い次元 (この場合は 3 次元) にマッピングして、境界を見つけ、分類を行うことでした。 しかし、次元が多くなると、その空間内での計算がどんどん高くなります。 このとき、カーネルのトリックが登場します。 高次元空間でのデータの座標を計算することなく、元の特徴空間で操作できるようになるのです。
例を見てみましょう。
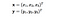
ここで x と y は3次元の2つのデータ点です。 x と y を 9 次元空間にマッピングする必要があると仮定しましょう。 最終的な結果は単なるスカラーですが、これを得るために以下の計算を行う必要があります。 この場合の計算量は、O(n²)である。

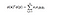
However, if we use the kernel function, which is denoted as k(x, y), instead of doing the complicated computations in the 9-dimensional space, we reach the same result within the 3-dimensional space by calculating the dot product of x -transpose and y. The computational complexity, in this case, is O(n).
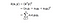
In essence, what the kernel trick does for us is to offer a more efficient and less expensive way to transform data into higher dimensions. With that saying, the application of the kernel trick is not limited to the SVM algorithm.
さまざまなカーネル関数
異なるカーネルが存在します。
「直感的には、多項式カーネルは、入力サンプルの与えられた特徴だけでなく、それらの類似性を判断するために、これらの組み合わせにも注目します」 (Wikipedia) と、ちょうど上記の例のようになります。 n 個の元特徴と d 度の多項式で、多項式カーネルは n^d 個の拡張特徴を生成します。
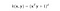
RBFカーネルはガウスカーネルとも呼ばれています。 特徴空間はテイラー級数で展開できるため、次元数は無限である。 以下の形式では、γパラメータは、1つの学習例がどれだけの影響を持つかを定義します。 大きくすればするほど、他の例も近い影響を受けなければならない(sklearnのドキュメント)。
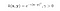
Pythonのsklearnライブラリには、カーネル関数にさまざまなオプションがあります。 必要に応じて、カスタム カーネルを構築することもできます。
おわりに
カーネルのトリックは「完璧」なプランのように聞こえます。 しかし、心に留めておくべき 1 つの重要なことは、データをより高い次元にマッピングするとき、モデルをオーバーフィットさせる可能性があるということです。
正則化とは何かについて興味がある方は、私の理解について述べた記事を書きましたので、こちらでご覧ください。
この記事を楽しんでいただければ幸いです。 お読みいただきありがとうございました。