ローパスフィルタとは何か？パッシブ RC フィルタの基礎に関するチュートリアル

12月 5, 2021admin

フィルタリングとは何でしょうか。

フィルタリングの概念を紹介し、抵抗-コンデンサ (RC) ローパスフィルタの目的と特性について詳しく説明します。

時間領域と周波数領域

オシロスコープで電気信号を見るとき、時間に対する電圧の変化を表す線が表示されているのがわかります。時間内の任意の瞬間、信号は1つの電圧値しか持ちません。

典型的なオシロスコープのトレースは、分かりやすく直観的ですが、信号の周波数成分を直接的に見ることができないため、やや限定的なものとなっています。

典型的なオシロスコープのトレースは、直感的ですが、信号の周波数成分を直接明らかにすることができないため、やや制限されます。時間領域表現とは対照的に、周波数領域表現（スペクトルとも呼ばれます）は、同時に存在するさまざまな周波数成分を識別することによって、信号に関する情報を伝達します。

正弦波（上）と方形波（下）の時間領域の表現。

正弦波 (上) と方形波 (下) の周波数領域の表現。

フィルターとは

フィルターは、特定の周波数成分を除去、または「フィルターアウト」する回路です。

周波数領域解析の経験があまりない場合、これらの周波数成分が何であるか、また、複数の電圧値を同時に持つことができない信号でどのように共存しているかについて、まだ不確かなことがあるかもしれません。

この概念を明確にするのに役立つ簡単な例を見てみましょう。

完全な 5 kHz の正弦波からなるオーディオ信号があると想像してみましょう。時間領域で正弦波がどのように見えるかは分かっていますし、周波数領域では、5 kHz での周波数の「スパイク」しか見えません。

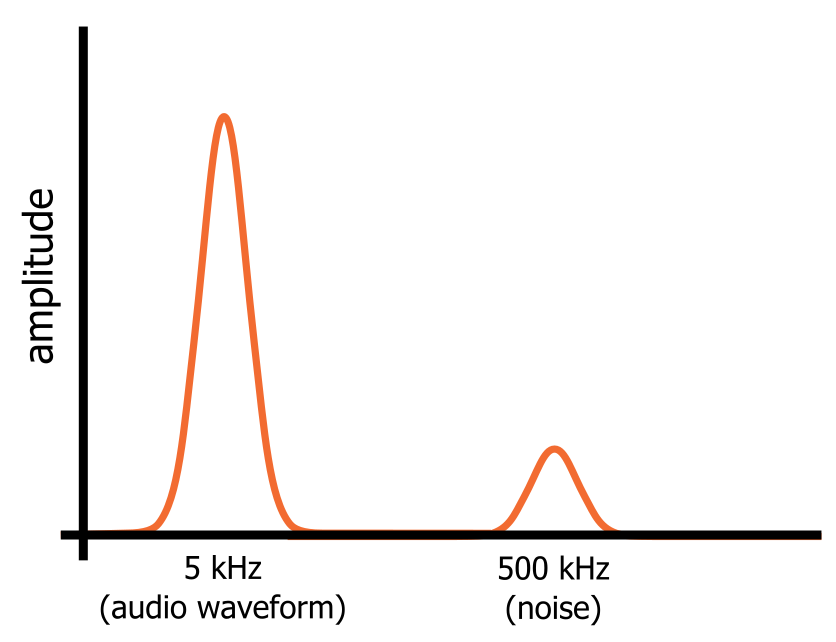
オシロスコープで見る信号は、時間の瞬間ごとに 1 つの値を持つ、一連の電圧にすぎませんが、時間領域の変動が 5 kHz の正弦波と高周波のノイズ変動の両方を反映しなければならないため、信号は異なって見えるでしょう。正弦波とノイズは、信号の周波数領域表現の異なる部分を占め (下図参照)、これは、低周波を通過させ高周波をブロックする回路に信号を導くことにより、ノイズを除去できることを意味します。

フィルターの種類

フィルターは、フィルターの周波数応答の一般特性に対応して、大きく分類することができます。フィルターが低周波を通過させ、高周波をブロックする場合、それはローパスフィルターと呼ばれます。低周波を遮断し、高周波を通過させるものはハイパスフィルターと呼ばれる。

フィルターは、回路を構成する部品の種類によっても分類されます。パッシブフィルタは抵抗、コンデンサ、インダクタを使用し、これらの部品は増幅する能力がないため、入力信号の振幅を維持または減少させることができるだけです。

このアクティブローパスフィルターは、一般的な Sallen-Key トポロジーをベースにしています

この記事では、パッシブローパスフィルターの解析と設計について説明します。

RC ローパス

パッシブローパスフィルターを作成するには、抵抗素子と反応素子を組み合わせる必要があります。言い換えれば、抵抗とコンデンサーまたはインダクターで構成される回路が必要です。理論的には、抵抗-インダクタ（RL）型ローパスと抵抗-コンデンサ（RC）型ローパスは、フィルタリング能力において同等である。

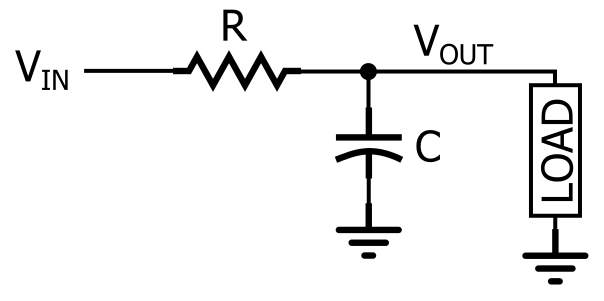
RC ローパスフィルター

図に示すように、RC ローパス応答は、抵抗を信号経路に直列配置し、コンデンサーを負荷に並列配置して作成されます。

抵抗とコンデンサーが周波数に依存する分圧器を形成していることを認識すれば、RC ローパストポロジーのフィルタリング動作を直観的に分析できます。

分圧器のように見えるように描き直した RC ローパスフィルター

入力信号の周波数が低い場合、コンデンサーは抵抗のインピーダンスに対して高いので、入力電圧のほとんどはコンデンサー (とコンデンサーと並列であるロード) で落とされます。入力周波数が高い場合、コンデンサのインピーダンスは抵抗のインピーダンスに対して低いので、抵抗により多くの電圧がかかり、負荷に伝わる電圧は少なくなる。

このようなRCローパス機能の定性的な説明は、最初のステップとして重要ですが、実際に回路を設計する際には、「高周波」「低周波」という言葉が非常に曖昧であるため、あまり役に立ちません。エンジニアは、特定の周波数を通過させたり遮断したりする回路を作る必要があるのです。例えば、先ほどのオーディオシステムで言えば、5kHzの信号を残し、500kHzの信号を抑えたい。

カットオフ周波数

フィルターが著しい減衰を引き起こさない周波数の範囲は通過帯域と呼ばれ、フィルターが著しい減衰を引き起こす周波数の範囲は停止帯域と呼ばれます。 RCローパスフィルタのようなアナログフィルタは、通過帯域から停止帯域まで常に徐々に変化する。つまり、ある周波数でフィルタの通過が止まり、信号が遮断されることを特定することは不可能である。

RC フィルターの周波数応答のプロットを見ると、「カットオフ周波数」という用語があまり正確でないことに気づかれるでしょう。

RCローパスフィルタのカットオフ周波数は、実際には入力信号の振幅が3 dB減少する周波数です (振幅の3 dB減少は電力の50%減少に相当するため、この値が選択されました)。したがって、カットオフ周波数は-3dB周波数とも呼ばれ、実際、この呼び名の方がより正確で、より情報量が多い。帯域幅という用語は、フィルターの通過帯域の幅を指し、ローパスフィルターの場合、帯域幅は -3 dB 周波数に等しくなります (下図参照)。

この図は RC ローパスフィルターの周波数応答の一般特性を伝えています。

上に説明したように、RC フィルターのローパス動作は、抵抗の周波数に依存しないインピーダンスとコンデンサの周波数に依存するインピーダンスの間の相互作用によって引き起こされます。フィルタの周波数特性の詳細を知るには、抵抗（R）と静電容量（C）の関係を数学的に解析する必要がありますが、これらの値を操作することで、正確な仕様に合致したフィルタを設計することも可能です。 RC ローパスフィルターのカットオフ周波数 (fC) は次のように計算されます:

単純な設計例を見てみましょう。コンデンサーの値は抵抗の値よりも制約が多いので、一般的な値の静電容量 (10 nF など) から始めて、式を使って必要な抵抗値を決定します。目標は、5kHzの音声波形を保持し、500kHzのノイズ波形を除去するフィルタを設計することです。記事の後半で、2 つの周波数成分に対するこのフィルターの効果をより慎重に分析します。

したがって、160 Ωの抵抗と 10 nF コンデンサーを組み合わせると、望ましい周波数特性に近いフィルターになります。

フィルター応答の計算

典型的な電圧分割器の計算の周波数依存バージョンを使用することにより、ローパスフィルターの理論的挙動を計算することができます。抵抗分圧器の出力は次のように表されます:

RC フィルターは同等の構造を使用しますが、R2の代わりにコンデンサーが使用されています。まず、R2 (分子) をコンデンサーのリアクタンス (XC) に置き換えます。次に、全インピーダンスの大きさを計算し、それを分母に置く必要がある。したがって、

コンデンサのリアクタンスは電流の流れに対する抵抗の大きさを示しますが、抵抗と違って、その大きさはコンデンサを通る信号の周波数に依存するのです。したがって、特定の周波数でのリアクタンスを計算する必要があり、これに使用する方程式は次のとおりです。

上記の設計例では、R ≈ 160Ω および C = 10 nF とします。ここでは、VINの振幅を1Vと仮定し、計算からVINを単純に取り除くことができるようにします。まず、正弦波の周波数における VOUT の振幅を計算してみましょう。

正弦波の振幅は基本的に変わりませんね。私たちの意図は、ノイズを抑制しながら正弦波を維持することでしたので、それは良いことです。正弦波の周波数（5 kHz）よりもはるかに高いカットオフ周波数（100 kHz）を選んだので、この結果は驚くことではありません。

次に、フィルターがノイズ成分をどれだけうまく減衰させるか見てみましょう。

ノイズ振幅は元の値の約 20% しかありません。

フィルター反応の視覚化

信号に対するフィルターの影響を評価するのに最も便利な方法は、フィルターの周波数応答のグラフを調査することです。横軸は通常対数スケールで、1 Hz と 10 Hz の間の物理的距離が、10 Hz と 100 Hz、100 Hz と 1 kHz の間の物理的距離と同じになるように設定されています。

周波数応答プロットの例

曲線上の各ポイントは、入力信号が 1 V の大きさを持ち、横軸の対応する値と同じ周波数を持つ場合の出力信号が持つ大きさを示しています。たとえば、入力周波数が 1 MHz の場合、出力振幅 (入力振幅が 1 V と仮定) は 0.1 V になります (-20 dB は 10 倍の減少に相当するため)。

この周波数応答曲線の一般形状は、フィルター回路をより長く使用すると、非常になじみやすくなっています。この曲線は、通過帯域ではほぼ完全に平坦で、入力周波数がカットオフ周波数に近づくにつれて、より急速に低下しはじめます。つまり、入力周波数が 10 倍になるごとに、出力信号の大きさが 20 dB ずつ減少します。

ローパス フィルタの性能評価

先に設計したフィルタの周波数応答を慎重にプロットすると、5 kHz における振幅応答が実質的に 0 dB (すなわち、, 減衰はほぼゼロ）、500 kHz での振幅応答は約 -14 dB です（これは 0.2 の利得に相当します）。

RCフィルタは通過帯域から阻止帯域まで常に緩やかに変化し、減衰が無限になることはないため、「完全な」フィルタ、つまり正弦波に影響を与えずノイズを完全に除去するフィルタを設計することはできないのです。その代わり、常にトレードオフの関係にある。カットオフ周波数を5kHzに近づけると、ノイズの減衰は大きくなりますが、スピーカーに送りたい正弦波の減衰も大きくなります。

ローパス フィルターによる位相変化

ここまで、フィルターが信号内のさまざまな周波数成分の振幅を変更する方法について説明してきました。

位相の概念は、周期内の特定の瞬間における周期的な信号の値を指します。つまり、ある回路が位相シフトを起こすということは、入力信号と出力信号の間にずれを生じさせるということであり、入力信号と出力信号はもはや同じ瞬間にそのサイクルを開始し、終了するわけではありません。 45° や 90° といった位相シフトの値は、どの程度のずれが生じたかを示します。

回路内の各反応エレメントは 90° の位相シフトをもたらしますが、この位相シフトは一度に起こるわけではありません。出力信号の位相は、出力信号の大きさと同様に、入力周波数が高くなるにつれて徐々に変化します。 RC ローパスフィルターでは、1 つの無効要素 (コンデンサー) があり、その結果、回路は最終的に 90° の位相シフトを導入します。

振幅応答と同様に、位相応答は、横軸が対数周波数を示すプロットを調べることで最も簡単に評価できます。

位相シフトは最初は 0°です。
それはカットオフ周波数で 45°に達するまで徐々に増加し、応答のこの部分の間、変化率は増加しています。
カットオフ周波数以降も位相シフトは増加し続けますが、変化率は減少します。
位相シフトが漸近的に 90°に近づくと、変化率は非常に小さくなります

実線は大きさの応答、点線は位相応答です。カットオフ周波数は100kHzです。

2次ローパス

ここまでは、RC ローパスフィルターが 1 つの抵抗と 1 つのコンデンサーで構成されていると仮定してきました。

パッシブフィルターの「次数」は、回路内に存在する反応要素 (すなわち、コンデンサーまたはインダクター) の数によって決定されます。高次のフィルターにはより多くの反応要素があり、これはより多くの位相シフトとより急なロールオフにつながります。

フィルターに 1 つの反応要素を追加することにより、たとえば、1 次から 2 次、または 2 次から 3 次へと、最大ロールオフを 20 dB/decade 増加させることができます。より急なロールオフは、低減衰から高減衰への移行がより速くなることを意味し、信号が目的の周波数成分とノイズ成分を分離する広い周波数帯域を持たない場合に、パフォーマンスの向上につながります。

2次フィルターは、一般に、コイルとコンデンサーからなる共振回路 (この位相は、抵抗器-コイル-コンデンサーで「RLC」と呼ばれます) を中心に構築します。しかし、2次RCフィルタを作ることも可能である。

このトポロジーは確かに2次応答を作成しますが、次のセクションで説明するように、周波数応答が2次アクティブフィルターや2次RLCフィルターよりも劣ることが多いため、あまり使用されません。

2次 RC フィルターの周波数特性

目的のカットオフ周波数に応じて1次フィルターを設計し、その1次ステージの2つを直列接続すれば、2次 RC ローパスフィルターを作ることが可能です。

しかし、応答をより詳細に見てみると、-3 dB 周波数が減少していることがわかります。 2 つのステージが独立していないため、2 次 RC フィルターは期待どおりに動作しません。これら 2 つのステージを単に接続して、1 次ローパスフィルターに続く同一の 1 次ローパスフィルターとして回路を分析することはできません。

2次RCローパスフィルターの基本的な制限は、設計者がフィルターのQファクターを調整することによって通過帯域からストップバンドへの移行を細かく調整できないことです。 2つの同じRCローパスフィルタをカスケード接続すると、全体の伝達関数は2次応答に相当しますが、Qファクターは常に0.5です。 Q=0.5の場合、フィルタはオーバーダンピングの境界線上にあり、その結果、遷移領域で周波数応答が「たるむ」ことになります。設計者は Q 係数を制御し、それによって遷移領域の周波数応答を微調整できます。

概要

すべての電気信号は、望ましい周波数成分と望ましくない周波数成分の混合物を含んでいます。望ましくない周波数成分は、通常、ノイズや干渉によって引き起こされ、状況によってはシステムの性能に悪影響を及ぼします。
フィルタは、信号のスペクトルの異なる部分に異なる方法で反応する回路です。
ローパスフィルターのカットオフ周波数は、フィルターが低減衰から大幅な減衰に移行する周波数領域を示します。
RC ローパスフィルタの出力電圧は、回路を (周波数に依存しない) 抵抗と (周波数に依存する) リアクタンスからなる分圧器として扱うことによって計算できます。
振幅 (dB 単位、縦軸) 対対数周波数 (ヘルツ単位、横軸) のプロットは、フィルタの理論動作を調べる便利で効果的な方法です。また、位相対対数周波数のプロットを使用して、入力信号に適用される位相シフトの量を決定できます。
2次フィルターはより急なロールオフを提供します。この2次応答は、信号が望ましい周波数成分と望ましくない周波数成分の間の分離の広いバンドを提供しない場合に有用です。全体の -3 dB 周波数は予想よりも低くなります。