年金支払い（PV）

admin
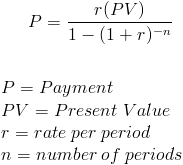
年金支払い式

年金支払い式は、年金の定期支払いを計算するために使用されています。 年金は、将来の日付で受信される一連の定期的な支払いです。 式の現在価値部分は最初の支払いであり、例として償却ローンの最初の支払いがあります。

示されている年金支払式は、通常の年金のためのものです。 この式は、利率が変わらず、支払額も変わらず、最初の支払いが1期先であると仮定しています。 比例配分で成長する年金は、成長する年金支払式を使用することになります。 それ以外の場合、支払額および/または利率を変更する年金は、変更のたびに調整する必要があります。 最初の支払いが最初にある年金は、年金支払式が使用され、繰延年金支払式は後日支払われることになります。

年金支払式は、償却ローン、収入年金、仕組み預金、宝くじの配当 (最初の支払いがすぐに始まる場合は年金支払式を参照)、およびその他のあらゆる種類の定期的な支払いに使用できます。

期間ごと

期間ごとの率と期間数は、支払いが行われる頻度を反映する必要があります。 たとえば、支払いが毎月であれば、毎月のレートが使用されるべきです。 同様に、期間数は月数であるべきです。 この概念は、すべての金融公式で覚えておくことが重要です。

年金支払式の説明

年金支払式は、年金式の PV を並べ替えることによって求めることができます。

Present Value of Annuity

After rearranging the formula to solve for P, the formula would become:

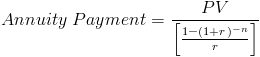
Solve for Payment

This can be further simplified by multiplying the numerator times the reciprocal of the denominator, which is the formula shown at the top of the page.

Return to Top

  • Formulas related to Annuity Payment
  • PV of Annuity
  • Loan Payment
  • Equivalent Annual Annuity
  • Annuity Payment Factor
  • Annuity Payment (FV)
  • Annuity Due Payment (PV)