補間の種類 – 利点と欠点
補間の方法
補間は、値がわかっている点またはサンプル点を使用して、他の未知の点での値を推定するプロセスです。
利用可能な補間手法は次のとおりです。 処理セルに近い点は遠い点より大きく重み付けされる。 指定された数のポイント、または指定された半径内のすべてのポイントは、各ロケーションの出力値を決定するために使用することができます。 このメソッドの使用は、マッピングされる変数がそのサンプリングされた位置からの距離で影響力が減少することを想定しています。 QGIS
IDW Interpolation; 提供 QGIS
IDW (Inverse Distance Weighting) アルゴリズムは、通常、非常に変動するデータに適用される移動平均補間法です。 特定のデータ タイプでは、収集場所に戻り、元の読み取り値とは統計的に異なるが、その地域の一般的な傾向の範囲内の新しい値を記録することが可能です。
移動平均法を使用して推定された補間表面は、ローカル最大値より小さく、ローカル最小値より大きくなります。

IDW 補間表面; 提供: ESRIESRI
IDW 補間では、互いに近いものは遠いものよりも似ているという仮定を明示的に実装しています。 任意の未測定位置の値を予測するために、IDW は予測位置の周囲の測定値を使用します。 予測地点に近い測定値は、遠い測定値よりも予測値に大きな影響を与える。 このように、IDWでは、各測定点には局所的な影響力があり、距離とともに減少すると仮定しています。 IDW関数は、解析に必要な局所的な表面変化の程度を把握するために、点群が十分に密集している場合に使用する必要があります。 IDWは、サンプル点の線形重み付けされた組み合わせセットを使用してセル値を決定します。
IDW 技術は、ユーザーが定義した検索半径内にある周囲のデータ ポイントを調べることによって、各グリッド ノードの値を計算します。 データポイントの一部または全部を補間処理に使用することができます。 ノードの値は、すべての点の加重和を平均して計算される。 ノードから徐々に離れていくデータポイントは、ノードに近いデータポイントよりも計算された値にはるかに影響を及ぼします。
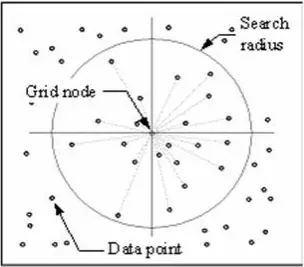
計算で使用するデータ ポイントを選択する、各グリッド ノードの周りに半径が生成されます。 Options to control the use of IDW include power, search radius, fixed search radius, variable search radius and barrier.
Note: The optimal power (p) value is determined by minimizing the root mean square prediction error (RMSPE).
Advantages
- Can estimate extreme changes in terrain such as: Cliffs, Fault Lines.
- Dense evenly space points are well interpolated (flat areas with cliffs).
- Can increase or decrease amount of sample points to influence cell values.
Disadvantages
- Cannot estimate above maximum or below minimum values.
- Not very good for peaks or mountainous areas.
Natural Neighbour Inverse Distance Weighted (NNIDW)
Natural neighbor interpolation has many positive features, can be used for both interpolation and extrapolation, and generally works well with clustered scatter points. もう一つの加重平均法で,自然隣人補間に使われる基本式はIDW補間に使われるものと同じです. この方法は、大規模な入力点データセットを効率的に処理することができます。
Natural Neighbor 法は、データ セット内の各点の周囲に生成された自然近傍領域を使用する幾何学的推定技法です。 しかし、距離で重み付けされたすべての入力点を使用して補間点の値を見つけるのではなく、自然隣人補間は入力点のドロニー三角形を作成し、補間点の周りに凸包を形成する最も近いノードを選択し、その値を面積で比例させて重み付けをします。 この方法は、サンプルデータ点が不均一な密度で分布している場合に最も適している。

Natural IDW: 提供: ESRI

この手法は、ポイント ファイルのローカル最小値と最大値を尊重し、ローカル最大値のオーバーシュートとローカル最小値のアンダーシュートを制限するように設定することが可能です。
利点
- 大量のサンプル ポイントを効率的に処理できます。
スプライン
スプラインは、全体の表面の曲率を最小化する数学関数を使用して値を推定し、入力ポイントを正確に通過する滑らかな表面を生成する

Spline: Courtesy: ESRI
概念的には、表面の総曲率を最小化しながら既知の点を通過するようにゴムのシートを曲げることに類似しています。 サンプルポイントを通過しながら、指定された数の最近接入力ポイントに数学的関数を当てはめる。 この方法は、標高、水位高さ、汚染濃度など、緩やかに変化する表面に最適である。
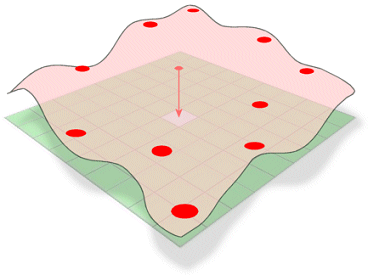
スプライン法には、正則化法とテンション法の 2 種類があります。
正社員化法は、サンプル データ範囲外の値を持つ、滑らかで徐々に変化する表面を作成します。
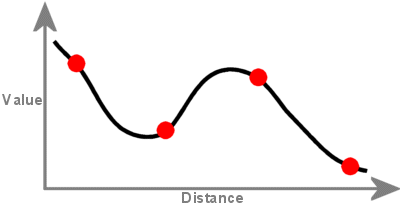
スプライン補間で作成されたサーフェスは、各サンプル ポイントを通過し、サンプル ポイント セットの値域を超える可能性があります。
Tension スプラインは 1 次および 2 次微分のみを使用しますが、スプライン計算により多くのポイントを含み、通常より滑らかなサーフェスを作成しますが計算時間が増加します。
スプライン補間に対する重みの選択
正則化スプラインです。 重みが高いほど、表面は滑らかになります。 0から5の間の重みが適しています。 典型的な値は 0、.001、.01、.1、.5 です。
Tension spline。 重みが大きいほど、表面は粗くなり、値はサンプル データの範囲に適合するようになります。 重みの値は0以上でなければなりません。 Typical values are 0, 1, 5, and 10.
Advantages
- Useful for estimating above maximum and below minimum points.
- Creates a smooth surface effect.
Disadvantages
- Cliffs and fault lines are not well presented because of the smoothing effect.
- When the sample points are close together and have extreme differences in value, Spline interpolation doesn’t work as well. This is because Spline uses slope calculations (change over distance) to figure out the shape of the flexible rubber sheet.
Kriging
Kriging is a geostatistical interpolation technique that considers both the distance and the degree of variation between known data points when estimating values in unknown areas. A kriged estimate is a weighted linear combination of the known sample values around the point to be estimated.
Z 値を持つ点の散在したセットから推定表面を生成するクリギング手順です。 Krigingは、サンプルポイント間の距離または方向が、サーフェスの変動を説明するために使用できる空間的相関を反映していると仮定しています。 Krigingツールは、指定された数の点、または指定された半径内のすべての点に数学的関数を当てはめ、各位置の出力値を決定します。 Krigingは多段階のプロセスです。データの探索的統計解析、バリオグラム・モデリング、曲面の作成、(オプションで)分散曲面の探索が含まれます。 Krigingは、データに空間的に相関した距離や方向性の偏りがあることが分かっている場合に最も適しています。 土壌学や地質学でよく使われます。
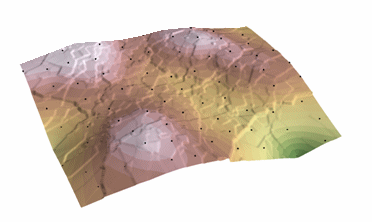
Kriging: Courtesy: ESRI
The predicted values are derived from the measure of relationship in samples using sophisticated weighted average technique. It uses a search radius that can be fixed or variable. The generated cell values can exceed value range of samples, and the surface does not pass through samples.
The Kriging Formula
Kriging is similar to IDW in that it weights the surrounding measured values to derive a prediction for an unmeasured location. The general formula for both interpolators is formed as a weighted sum of the data:
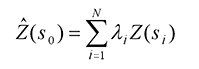
- where:
Z(si) = the measured value at the ith location
λi = an unknown weight for the measured value at the ith location
s0 = the prediction location
N = the number of measured values
In IDW, the weight, λi, depends solely on the distance to the prediction location. しかし、クリギング法では、測定点から予測位置までの距離だけでなく、測定点の空間的な配置を総合的に判断して重みを決定する。 重みに空間配置を用いるためには、空間的な自己相関を定量化する必要がある。 したがって、通常のクリギングでは、重みλiは、測定点への適合モデル、予測地点までの距離、予測地点周辺の測定値間の空間的関係に依存する。 以下では、一般的なクリギング式を使って、予測曲面のマップと予測精度のマップを作成する方法について説明します。
クリギングの種類
通常のクリギング
通常のクリギングはモデル
Z(s) = µ + ε(s),
μは未知の定数と仮定しています。 通常のクリギングに関する主な問題の1つは、平均が一定であるという仮定が妥当かどうかということです。 Sometimes there are good scientific reasons to reject this assumption. However, as a simple prediction method, it has remarkable flexibility.
Ordinary kriging can use either semivariograms or covariances, use transformations and remove trends, and allow for measurement error.
Simple Kriging
Simple kriging assumes the model
Z(s) = µ + ε(s),
where µ is a known constant.
Simple kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Universal Kriging
Universal kriging assumes the model
Z(s) = µ(s) + ε(s),
where µ(s) is some deterministic function.
Universal kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
インディケータ・クリギング
インディケータ・クリギングはモデル
I(s) = µ + ε(s),
ここでµは未知数でI(s)は2値変数である。 バイナリデータの作成は、連続データの閾値の使用による場合もあれば、観測されたデータが0か1かの場合もあります。 例えば、ある地点が森林か非森林の生息地であるかどうかの情報からなるサンプルがあり、バイナリ変数がクラス・メンバーシップを示すとする。
Indicator Krigingは、半変量または共分散を使うことができます。
確率クリギング
Probability Krigingはモデル
I(s) = I(Z(s) > ct) = µ1 + ε1(s)Z(s) = µ2 + ε2(s),
ここでμ1とμ2は未知定数、I(s)は閾値を使った二値変数です。 I(Z(s) > ct)とする。 ここで、ランダム誤差はε1(s)とε2(s)の2種類あるので、それぞれに自己相関があり、それらの間に相互相関があることに注意してください。 確率的クリギングは指標的クリギングと同じことをしようとするものですが、より良い仕事をするためにコクリギングを使っています。
Probability Krigingは、半変量または共分散、交差共分散、変換のいずれかを使用できますが、測定誤差を許容することはできません。
style=”display:inline-block;width:468px;height:60px” data-ad-client=”ca-pub-7134201556760050″ data-ad-…slot=”9271753327″>
Disjunctive Kriging
Disjunctive Krigingでは、以下のように仮定されます。 モデル
f(Z(s)) = µ1 + ε(s),
ここで、μ1 は未知の定数、f(Z(s))は Z(s)の任意の関数である。 f(Z(s)) = I(Z(s) > ct)と書けるので、インディケータ・クリギングは分離型クリギングの特殊ケースであることに注意しましょう。 Geostatistical Analystでは、値そのものを予測することも、指標を予測することも、分離型クリギングで可能です。
一般に、分離型クリギングは通常のクリギングより多くのことを行おうとします。 報酬は大きいかもしれませんが、その分コストもかかります。 Disjunctive kriging requires the bivariate normality assumption and approximations to the functions fi(Z(si)); the assumptions are difficult to verify, and the solutions are mathematically and computationally complicated.
Disjunctive kriging can use either semivariograms or covariances and transformations, but it cannot allow for measurement error.
Advantages
- Directional influences can be accounted for: Soil Erosion, Siltation Flow, Lava Flow and Winds.
- Exceeds the minimum and maximum point values
Disadvantages
- Does not pass through any of the point values and causes interpolated values to be higher or lower then real values.
** Kriging の数学的アプローチについての深い洞察は、補間手法の Kriging をクリックしてください。
PointInterp
IDW に似た手法で、PointInterp 機能はサンプリング周辺をより制御できるようにします。 補間されたグリッド セル値に対する特定のサンプルの影響は、サンプル ポイントがセルの近傍にあるかどうか、および補間されるセルからどのくらい離れているかに依存します。

PointInterp; Courtesy: ESRI
近隣内のポイントの重み付け値は、逆距離重み付け補間または逆指数距離補間を使用して計算されます。 この方法は、点状特徴を使用してラスターを補間しますが、さまざまな種類の近傍領域を使用できます。 近傍は、円、矩形、不規則な多角形、環状、または楔などの形状を持つことができます。
Trend
Trend は最小二乗回帰適合を用いてサンプル ポイントに適合する表面を見つけ出す統計的手法です。 これは、1つの多項式をサーフェス全体に当てはめます。 その結果、入力値に対するサーフェスの分散を最小化するサーフェスが得られる。 サーフェスは、すべての入力点について、実際の値と推定値の差の合計(すなわち分散)ができるだけ小さくなるように構築される。

Trend; Courtsey:ESRI
不完全な補間であり、結果の表面が入力点を通過することは稀です。 しかし、この方法はサンプル データの傾向を検出し、一般的に滑らかに変化する自然現象に似ています。
利点
- 傾向曲面は、データ内の粗いスケールのパターンを識別するのに適しています; 補間表面はサンプル ポイントをほとんど通り抜けません。
Topo to Raster
Topo to Raster 法は、ラスターの標高値を補間することにより、接続された排水構造を含む水文学的に正しいデジタル標高モデル、および入力コンター データから尾根とストリームを正確に表現できるようにするための制約を課すものです。 また、反復有限差分補間の手法を用いることで、大局補間の面連続性を損なうことなく、局所補間の計算効率を最適化することができます。 特に、輪郭入力に対してインテリジェントに動作するように設計されています。
Topo to Raster 補間を使用して、標高点、等高線、ストリーム ライン、および湖ポリゴンから補間されたサーフェスの例を次に示します。
Topo to raster; Courtesy: ESRI
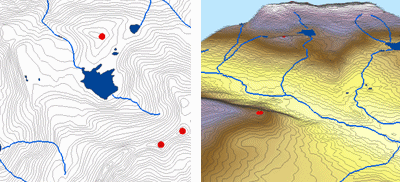
Topo to Raster は、標高ポイント、等高線、ストリーム ライン、湖ポリゴン、シンク ポイント、および調査領域境界ポリゴンなどの地形コンポーネントのベクトル データから水文学的に正しいラスター サーフェスを作成する特殊ツールです。
Density
Density ツール(ArcGIS で使用可能)は、単位面積あたりのあるものの量または数を示すサーフェスを作成します。 密度ツールは、一連の観察から野生生物の個体数の分布を表す密度サーフェスを作成したり、道路の密度から地域の都市化の度合いを表現したりするのに便利です。

Density Raster; Courtest: ERSI
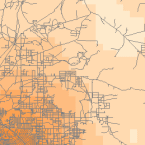
Density and Roads; Courtesy: ESRI
There are density tools for point and line features in ArcGIS.
Related Topics
- What is Interpolation ?
- Classification of Interpolation Techniques.
- Choosing the Right Interpolation Method