限界分布

確率分布 > 限界分布

限界分布とは何か

以下のビデオを見るか記事を読んでください：

技術的な定義は、見ていて少し頭が痛くなります:

限界分布の定義 = X と Y を離散確率変数、f (x,y) を (x,y) における
両者の結合確率分布の値とすると、以下の関数によって与えられるものです。
g(x) = Σy f (x,y) と h(y) = Σx f (x,y) はそれぞれXとYの限界分布である。

方程式が得意なら、おそらくこれだけ知っていれば十分でしょう。 これは、周辺分布を見つける方法を教えてくれます。

限界分布は、確率分布表の余白に表示されることからその名前がつきました。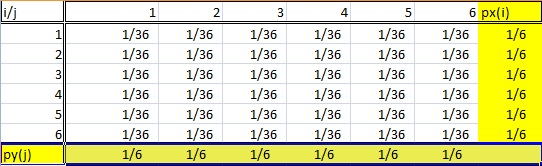

もちろん、これほど単純ではありません。 古い度数分布表を見て、最後の列 (または行) が “限界分布” である、と言うことはできないのです。 限界分布はいくつかのルールに従います:

• 分布は二変量データからのものでなければなりません。 上の表では、確率変数 i と j は 2 つのサイコロの目から得られています。
• 限界分布は、確率変数の 1 つだけに興味がある場合です。 言い換えれば、X か Y のいずれかです。上の確率表を見ると、1 つの変数の合計確率が下の行に、他の合計確率が右の列にリストアップされています。

限界分布と条件付き分布の違い

条件付き分布は、データ セット全体の特定のサブ集団にのみ興味がある場合です。 サイコロを振る例では、これは、「2を振る」または「6を振る」かもしれません。 下の画像は、2 つの強調された部分集団 (したがって、2 つの条件付き分布) を示しています。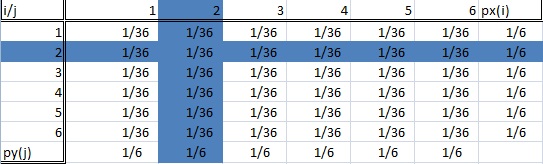

限界分布確率を計算する方法

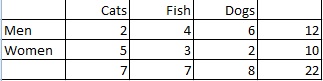
例題を挙げましょう。
解答：
ステップ1：総人数を数えます。
ステップ2：各ペットの種類を好む人の数を数え、その比率を確率に変える：
猫を好む人：7/22 = .32
魚を好む人：7/22 = .32
犬を好む人：8/22 = .36
ヒント：確率がすべて1に加算されるかどうか確認することで答えを確認できます。

質問2（相互排他事象）です。 P(A) = 0.20, P(b) = 0.70, および両方のイベントが相互に排他的である場合, P(B’∩A), P(B’∩A’) および P(B’) を求める。
この表記に慣れていない場合, P(A’) とは “not A”, または補語を意味しています.

Answer:
確率は個別に計算できますが、表を使って計算する方がはるかに簡単です。

ステップ 1: 与えられた情報で頻度表を記入します。 確率の合計は1になるはずなので、それを余白（合計）に加えてもよいでしょう。 単純な足し算・代数で余白を埋めます。 例えば、一番下の行では、0.70 + x = 1.00 なので、B’ の余白合計は 0.30 でなければなりません。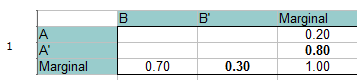

ステップ 2: 表の左上で、AとBの交点を0と追加します。

Step 3: 残りの空欄を簡単な足し算・代数で埋めていきます。

表から読み解く（2つの記載確率の交点を見る）：
P（B’∩A）=0.20
P（B’∩A’) = 0.10
P（B∩A’) = 0.70.

例題3（独立事象）…

例題3（独立事象）…B’∩A（B’∩A’) = 0.70.
B’∩A（B’∩A’) = 0.70.p P(A)=0.20, P(b)=0.70, 両イベントが独立である場合、P(B’∩A), P(B’∩A’), P(B∩A’) を求める

解答です。 今回はAとBが独立しているので、両方が同時に起こる確率は0.14（P(A)*P(B) = 0.20 * 0.70 = 0.14）である。 この値は左上（AとBの交点）に入る。 表の残りを上記の手順とまったく同じように記入します。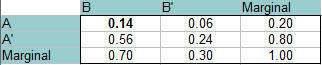

表から答えを読み取ります (2 つの確率の交差点から):
P(B’∩A): 0.06
P(B’∩A’): 0.24
P(B∩A’): 0.56.

Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, pp.536 and 571, 2002.
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Lindstrom, D. (2010).「統計学」. Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 第2版. McGraw-Hill Education

————————————————————–

宿題やテストの質問で助けが必要ですか？ Chegg Studyでは、その分野の専門家からステップバイステップの解決策を得ることができます。 Cheggのチューターとの最初の30分間は無料です!