電磁波
理論編
Maxwell’s equationsEdit
James Clerk Maxwell は、電場と磁場の方程式を波状に導き、電場と磁場の波状性とその対称性を明らかにしました。 波動方程式によって予測される電磁波の速度は、測定された光の速度と一致したため、マクスウェルは光そのものが電磁波であると結論づけた。
マクスウェルの方程式によれば、空間的に変化する電場は、常に時間的に変化する磁場を伴っている。
マクスウェルの方程式によれば、空間的に変化する電場は、時間とともに変化する磁場を常に伴っています。同様に、空間的に変化する磁場は、電場の特定の時間的変化に関連しています。 電磁波では、電場の変化には必ず一方向の磁場の波が伴い、その逆もまた然りである。 この両者の関係は、どちらかのタイプの電場がもう一方を引き起こすことなく、むしろ特殊相対性理論において時間と空間の変化が共に起こり、連動しているのと同じように起こる。 実際、磁場は別の参照枠では電場、電場は別の参照枠では磁場と見ることができるが、物理学はどの参照枠でも同じなので、ここでいう空間と時間の変化の密接な関係は単なるアナロジーに過ぎないのである。 これらの場が一緒になって伝播する電磁波を形成し、空間に移動して、二度と発生源と相互作用する必要がない。
近接場と遠方場

マクスウェルの方程式は、いくつかの電荷と電流(「ソース」)が EMR の挙動を持っていないそれらの近くに電磁界の局所的なタイプを生成することを確立しました。 電流は直接磁場を発生させますが、それは磁気双極子型であり、電流から離れると消滅します。 同様に、電位の変化により導体中を移動する電荷(アンテナなど)は、電気双極子型の電界を発生するが、これも距離が離れると減少する。 このような電界が電磁波発生源付近の近傍界を構成している。 いずれも電磁波を発生させるものではありません。 むしろ、変圧器内部の磁気誘導や金属探知機のコイルの近くで起こるフィードバック動作のように、発生源に非常に近い受信機にのみ効率的に電力を伝達する電磁界挙動を引き起こします。 一般に、近接場はそれ自身の発生源に強力な影響を及ぼし、受信機によって電磁場からエネルギーが引き出されるたびに、発生源または送信機の「負荷」の増加(電気的リアクタンスの減少)を引き起こします。
対照的に、EM 遠距離場は、(電気変圧器の場合とは異なり)送信機が、信号がすぐに拾われるかどうかにかかわらず、場のこれらの変化を外に送るために同じ電力を必要とするという意味で、送信機から自由である放射で構成されています。 この電磁場の遠い部分が「電磁放射」(ファーフィールドとも呼ばれる)である。 ファーフィールドは、送信機の影響を受けずに伝播(放射)していきます。 このため、送信機から離れた後の存在やエネルギーは、送信機と受信機の両方から完全に独立しているという意味で、独立した存在となります。 エネルギー保存則により、発信源の周囲に描かれたどの球面を通過する電力量も同じである。 このような表面は、発信源からの距離の二乗に比例した面積を持つので、EM放射の電力密度は常に発信源からの距離の逆二乗とともに減少する。これは逆二乗の法則と呼ばれる。
遠方電磁界(EMR)は、近傍電磁界とは異なるメカニズムで、マクスウェル方程式の異なる項によって生成されています。 近接場の磁場が発生源の電流に起因するのに対し、EMR の磁場は電場の局所的な変化のみに起因します。 同様に、近接場の電場は発生源の電荷と電荷分離に直接起因するのに対し、EMRの電場は局所的な磁場の変化に起因する。 EMRの電場と磁場の生成過程は、いずれも近接場双極子電場と磁場とは距離に対する依存性が異なっている。 そのため、EMR型の電磁界は、発生源から「遠い」電力で支配的になるのです。 光源から遠い」とは、光源電流が光源電位の変化によって変化し、光源が異なる位相の外向き電磁場を生成し始めるまでに、外向き電磁場のどの部分も光源からどれだけ離れているか(光速で動いているか)という意味である。
EMRのよりコンパクトな見解は、EMRを構成する遠距離場は一般に、ソースから十分な距離を移動したEMフィールドの一部であり、元々それを担当していた電荷や電流へのフィードバックから完全に切り離されたものであるということです。 電磁場は、発生源の電荷から独立し、遠ざかるにつれて、それを発生させた電荷の加速度だけに依存するようになる。
(マクスウェルの方程式による) 単一の粒子の運動による電場および磁場のリエナール ウィヒェルト ポテンシャル定式化では、粒子の加速に関連する項が、電磁放射とみなされる電場の部分を担っています。 これに対して、粒子の静電場の変化に伴う項と、粒子の一様な速度に起因する磁気項は、いずれも電磁波の近接場に関するものであり、電磁波を構成するものではありません。
PropertiesEdit

電磁気学は電磁波の物理学であり、電磁気学は電磁気学の理論に関連する物理現象です。 電場と磁場は重ね合わせの性質に従います。 したがって、ある特定の粒子による場、あるいは時間的に変化する電場や磁場は、他の原因によって同じ空間に存在する場に寄与することになる。 また、ベクトル場であるため、磁場や電場のベクトルはベクトル加算によってすべて足し合わされます。
光の電磁場は、真空のような直線的な媒体では、静的な電場や磁場を通過しても影響を受けません。
屈折では、ある媒体から密度の異なる別の媒体に渡る波は、新しい媒体に入るときにその速度と方向を変えます。 媒質の屈折率の比が屈折の度合いを決定し、スネルの法則でまとめられる。 複合波長の光 (自然光) がプリズムを通過すると可視光に分散するのは、プリズム材料の屈折率が波長に依存するため (分散)、つまり複合光内の各成分波が異なる量だけ曲げられるからです。
EM放射は波の性質と粒子の性質を同時に示します (「波粒子双対性」を参照)。
電子放射は、波と粒子の性質を同時に示す(波動・粒子双対性参照)。 波の性質は、電磁波を比較的大きな時間スケールと大きな距離で測定した場合に現れ、粒子の性質は小さな時間スケールと距離で測定した場合に現れます。 例えば、電磁波が物質に吸収されるとき、波長の3乗に含まれる光子の平均数が1よりずっと小さいと、粒子的な性質が顕著に現れる。光が吸収されるとき、エネルギーが不均一に沈むのを実験的に観察することはそれほど難しくないが、それだけでは「粒子的」行動の証拠とはならない。 むしろ、物質の量子的な性質を反映しているのです。
単一光子の自己干渉のように、電磁波の波動性と粒子性の両方を示す実験もあります。
電磁波と電子などの物質との相互作用の量子論は、量子電気力学の理論によって記述されます。
電磁波は、偏光、反射、屈折、回折、または互いに干渉することができます。
波動モデル編集

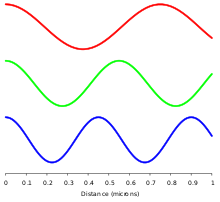
均質な等方性媒体において、電磁放射は横波であり、その振動はエネルギーの伝達および移動の方向に対して垂直であることを意味します。 電場と磁場の部分は、一方が他方からどのように生成されるかを規定する2つのマクスウェル方程式を満たすために、強さの一定の比率で立っています。 散逸のない(ロスのない)媒質では、これらの電場と磁場も同位相で、空間上の同じ地点で最大と最小になります(図参照)。 よくある誤解は、電磁波のE場とB場は位相がずれている、なぜなら一方が変化すると他方も変化し、正弦波関数として両者の間に位相差が生じるからだというものです(実際、電磁誘導やアンテナ近傍の近距離場ではそうなっているのですが)。 しかし、2つのソースのないマクスウェル・カール演算子方程式で記述される遠距離電磁放射では、より正しい記述は、一方のタイプの磁場の時間変化が他方の空間変化に比例することである。 これらの導関数は、EMR の E および B 磁場が同相であることを必要とします (下記の数学のセクションを参照)。
光の性質の重要な側面として、その周波数が挙げられます。
光の性質で重要なのはその周波数です。波の周波数は振動数で、SI単位であるヘルツで表されます。 光は通常、複数の周波数を持っており、それが合計されて波となる。
単色波(単一周波数の波)は、連続した谷と山からなり、隣接する2つの山または谷の間の距離を波長と呼びます。 電磁波の大きさは、大陸より長い電波から原子核より短いガンマ線までさまざまである。 周波数は波長に反比例し、次の式で表される。

ここでvは波の速度(真空ではc、他の媒体ではそれ以下)、fは周波数、λは波長です。
自由空間における電磁波は、マクスウェルの電磁波方程式の解でなければなりません。 解には大きく分けて平面波と球面波の2種類が知られています。 平面波は、ソースから非常に大きな(理想的には無限)距離で球面波の限界ケースとして見ることができます。 どちらの波も、波動方程式に適合するように十分に微分可能であれば、任意の時間関数で波形を作ることができます。 時間関数と同様に、フーリエ解析によって周波数スペクトル、つまり各々が単一の周波数、振幅、位相を持つ正弦波成分に分解することができる。 このような成分波は単色波と呼ばれる。
干渉とは、2つ以上の波が重なり合い、新しい波形を生み出すことです。
干渉とは、2つ以上の波が重なり合い、新たな波形を生み出すことです。磁場の成分が同じ方向であれば、建設的に干渉し、反対方向であれば破壊的に干渉します。 EMRによる干渉の例として、EMI(電磁妨害)、RFI(高周波妨害)などがある。
電磁波のエネルギーは、放射エネルギーと呼ばれることもあります。
粒子モデルと量子論
19世紀後半に、光の波動理論と、黒体として知られる熱放射体から放射される電磁スペクトルの測定との間に矛盾が生じるという異常事態が発生しました。 物理学者たちは、この問題に何年も取り組みましたが、うまくいきませんでした。 この問題は、後に「紫外線のカタストロフィー」と呼ばれるようになる。 1900年、マックス・プランクは、観測されたスペクトルを説明する新しい黒体放射の理論を開発した。 プランクの理論は、黒体が光(およびその他の電磁波)を放出するのは、エネルギーの不連続な束またはパケットのみであるという考えに基づいている。 このパケットは「量子」と呼ばれる。 1905年、アルバート・アインシュタインが、光量子を実際の粒子と見なすことを提案した。 その後、光の粒子は、電子や陽子など、この頃に記述された他の粒子と対応して、光子と呼ばれるようになった。 光子のエネルギーはEで、周波数fに比例し、次のように表される
E = h f = h c λ {hrac {hc}{lambda }},\!

ここでhはプランク定数、λ {displaystyle \lambda }である。

は波長、cは光の速さです。 プランク-アインシュタイン方程式と呼ばれることもあります。 量子論では(最初の量子化を参照)、光子のエネルギーはこのように電磁波の周波数に正比例します。
同様に、光子の運動量 p もその周波数に比例し、波長に反比例します:
p = E c = h f c = h λ . {displaystyle p={E \over c}={hf \over c}={h \over }.}
光子の運動量pは周波数に反比例し、波長に比例します。

光が粒子からなる(あるいは状況によっては粒子として作用する)というアインシュタインの提案の源は、金属表面に当たった光が表面から電子を出して、電圧をかけたところに電流が流れているという光電効果という波の理論では説明できない実験の異変にありました。 その結果、放出される個々の電子のエネルギーは、光の強さではなく、周波数に比例することが実験的に明らかになった。 さらに、金属によって異なるが、ある最小周波数以下では、光の強さに関係なく電流が流れないこともわかった。 これらの観測結果は、波動説と矛盾するように見え、物理学者たちは何年もその説明を試みた。 1905年、アインシュタインは、光の粒子説を復活させて、この謎を説明した。 しかし、波動説を支持する証拠が多数あったため、アインシュタインの考えは、当初、既存の物理学者の間で大きな懐疑的な目で見られた。
光子が原子に吸収されると、原子が励起され、電子がより高いエネルギーレベル(平均して原子核からより遠いレベル)に上昇します。 励起された分子や原子の電子が低いエネルギー準位に下がると、そのエネルギー差に対応する周波数の光を放出するのです。 原子の電子のエネルギー準位はバラバラなので、元素ごと、分子ごとに特徴的な周波数を放出・吸収している。 即座に光子が放出されることを蛍光といい、フォトルミネセンスの一種である。 例えば、蛍光塗料が紫外線(ブラックライト)に反応して発する可視光はその一例である。 このほか、可視光以外の波長帯でも多くの蛍光発光が知られている。
波動-粒子二重性
光の性質を説明する現代の理論には、波と粒子の二重性という考え方があります。 より一般的には、すべてのものは粒子の性質と波の性質の両方を持っており、さまざまな実験によってどちらかを引き出せるとする理論です。 粒子の性質は、大きな質量を持つ物体を使うとより分かりやすい。 1924 年の Louis de Broglie による大胆な提案により、科学界は物質(電子など)も波動と粒子の二面性を示すことに気づきました。
電磁波の波動効果と粒子効果
波動効果と粒子効果は、合わせて電磁波の放射および吸収スペクトルを完全に説明することができます。 光が通過する媒体の物質組成は、吸収と放出スペクトルの性質を決定する。 このスペクトルは、原子のエネルギー準位に対応する。 吸収スペクトルの暗黒帯は、光源と観測者の間に介在する媒質中の原子に起因するものです。 原子は、光源と検出器/目の間の光の特定の周波数を吸収し、すべての方向に放出する。 検出器には、ビームから散乱された放射による暗黒帯が現れます。 例えば、遠くの星が放つ光にダークバンドがあるのは、星の大気に含まれる原子のせいである。 発光も同じような現象で、発光しているガスが熱など何らかの原因で原子が励起され、光って見えるのです。 電子が低いエネルギー準位に降下すると、電子のエネルギー準位間のジャンプを表すスペクトルが放出されるが、励起後特定のエネルギーでのみ再び発光が起こるため、線が見られるようになる。 例として、星雲の発光スペクトルが挙げられる。
これらの現象は、背後から照らされた気体の組成(吸収スペクトル)や、発光している気体の組成(発光スペクトル)など、さまざまな化学的決定に役立っているのです。 例えば、ある星がどのような元素で構成されているかは、分光観測によって決定されます。
伝搬速度
電線(またはアンテナなどの導電体)が交流電流を流すと、電流と同じ周波数で電磁波が伝搬されます。 このような状況の多くでは、励起電位による電荷の分離から生じる電気双極子モーメントを特定することが可能で、この双極子モーメントは電荷が前後に動くと、時間的に振動する。
量子レベルでは、荷電粒子の波束が振動するか、さもなければ加速すると、電磁波が発生します。
量子レベルでは、荷電粒子の波束が振動したり、加速したりすると電磁波が発生します。静止状態の荷電粒子は動きませんが、そのような状態の重ね合わせによって、時間的に振動する電気双極子モーメントを持つ遷移状態になることがあります。 この振動する双極子モーメントが、荷電粒子の量子状態間の放射遷移の現象に関与している。
波としての光は、速度 (光速)、波長、および周波数によって特徴付けられます。
光は波として、速度(光速)、波長、周波数によって特徴づけられます。 ここで、Eは光子のエネルギー、hはプランク定数、6.626×10-34J-s、fは波の周波数です。
1つのルールは、どんな状況でも守られます。 真空中の電磁波は、観測者の速度に関係なく、観測者に相対して光速で伝わる。 (真空中の電磁波は、観測者の速度に関係なく、観測者に相対して光速で進むのです(この観測により、アインシュタインは特殊相対性理論を開発しました)。(真空以外の)媒体では、周波数と用途に応じて、速度係数または屈折率を考慮します。
特殊相対性理論
19世紀後半になると、様々な実験的異常が単純な波動理論では説明できなくなりました。 その1つが光速をめぐる論争です。 マクスウェルの方程式で予測される光や他の電磁波の速度は、方程式がフィッツジェラルドとローレンツによって最初に提案された方法で修正されない限り現れず(特殊相対性理論の歴史を参照)、さもなければその速度は、電磁波を「運ぶ」(空気が音波を運ぶのと同様の方法で)「媒体」(ルミファーエーテルという)への観測者の相対速度に依存することになります。 しかし、実験では観測者効果を見出すことはできなかった。 1905年、アインシュタインは、光の伝播やその他すべてのプロセスや法則において、空間と時間は速度変更可能な存在に見えると提唱した。 これらの変化は、すべての観測者 (相対運動している観測者を含む) の視点から、光速とすべての電磁放射が一定であることを説明したのです
。