dBである。 デシベルとは何ですか？
音圧、サウンドレベル、dB。 音は通常マイクロホンで測定され、それらは音圧pに比例して反応します。さて、音波のパワーは他のすべてが同じで、音圧の二乗に比例します。 (同様に、抵抗器の電力は電圧の2乗に比例する）。 x2の対数はちょうど2 log xなので、音圧比をデシベルに変換するときに2の係数が発生します。 したがって、p1とp2の2つの音の音圧レベルの差は、次のようになります。
20 log (p2/p1) dB = 10 log (p22/p12) dB = 10 log (P2/P1) dB (全体として、対数は 10 ベース)
音響パワーを半分にするとどうなるでしょうか。 2のlogは0.3010ですから、1/2のlogは近似的に-0.3です。 つまり、パワーを半分にすると、パワーと音量を3dB減らすことができるのです。 もう一度半分にすると（元のパワーの1/4にする）、さらに3dBレベルが下がります。 電力を半分にし続けると、このような比率になります。
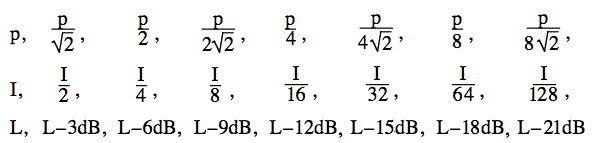
同じ音を 2 つ追加するとどうなるでしょうか。 強さは 2 倍になりますか (3 dB の増加)。 それとも音圧を 2 倍にしますか (6 dB の増加)。 このよくある質問は少し微妙なので、この FAQ で説明します。
デシベルの大きさを示すサウンド
上で、出力を半分にすると音圧が√2、サウンド レベルが 3 dB 減少することを確認しました。 これは、以下の最初のグラフィックとサウンド ファイルで行ったことです。
|
1デシベルは音量のJNDと同じ桁の値です。 これらのファイルを聴くと、最後のものが最初のものより静かであることに気づきますが、どのペアの2番目も前のものよりも静かであることは、耳にはあまりわかりません。 10*log10(1.26) = 1なので、音量を1dB上げるには、電力を26％、電圧を12％上げる必要があります。 |
もし差が1デシベル以下ならどうでしょうか? 音の大きさが小数点以下の数値で示されることはほとんどありません。 次の例が示すように、1 dB 未満の音の違いは区別しにくいからです (このため、dB は便利な大きさの単位になっています)。
| 0.3 dB ステップ。 最初の組より最後の組の方が静かであることに気づくかもしれませんが、連続した組の差は気づきにくいものです。 10*log10(1.07) = 0.3なので、音量を0.3dB上げるには、電力を7%、電圧を3.5%上げる必要があります。
|
標準の基準値について (‘絶対’ 音量)
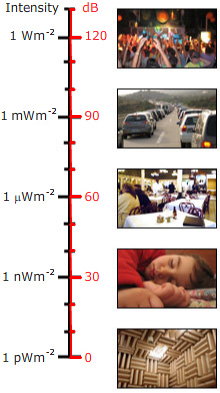デシベルは比率であると上記で述べました。 そこで、比率ではなく、一つの音のレベルを示すために用いる場合、基準となるレベルを選ぶ必要があります。 音圧レベルの場合、基準レベル（空気の場合）は通常、pref=20マイクロパスカル（20μPa）、つまり0.02mPaとして選ばれます。 これは非常に低い値で、大気の100億分の2である。 しかし、これは人間の耳の感度の限界であり、周波数が敏感な範囲である。 (通常、このような感度は、比較的若い人や、大音量の音楽や騒音にさらされていない人にしか見られません。 イヤースピーカー付きのパーソナルミュージックシステムは、耳元で非常に高い音量を出すことが可能であり、ある国の若年層の難聴の原因の多くを占めていると考えられている)。
つまり、音圧レベルが 86 dB である場合、
20 log (p2/pref) = 86 dB
ここで pref は基準レベルの音圧、p2 は問題のサウンドの音圧です。 両辺を 20 で割ると
log (p2/pref) = 4.3
p2/pref = 104.3
4 は 1 万の対数、0.3 は 2 の対数なので、この音の音圧は基準レベルの 2 万倍 (p2/pref = 2 万)、強さは基準レベルの 4 億倍となるのです。 86dBは大きな音ですが、短時間であれば危険ではありません。
0dBとはどういう意味ですか？ すなわち、0.02mPaに相当する音圧レベルである。 この場合、
サウンド レベル = 20 log (pmeasured/pref) = 20 log 1 = 0 dB
デシベルは比率を測定するものであることを思い出してください。 0 dB は、比が 1 の対数をとったときに発生します (log 1 = 0)。 つまり、0dBは音がないという意味ではなく、音圧が基準レベルの音圧と等しくなる音量を意味します。 これは小さな圧力ですが、ゼロではありません。 20dBは、基準圧力の10倍小さい圧力、すなわち2μPaの音を意味します。
すべての音圧が同じ大きさであるわけではありません。 人間の耳はすべての周波数に等しく反応するわけではないからです。非常に低い周波数や高い周波数の音よりも、約1kHz～7kHz（1秒間に1000～7000回振動する）の周波数帯の音にはるかに敏感に反応するのです。 このため、騒音計には通常、周波数に対する反応が人間の耳の反応に少し似たフィルターが取り付けられている。 (A特性フィルタ」を使用した場合、音圧レベルはdB(A)またはdBAの単位で表示されます。 dBAスケールの音圧レベルは測定が容易であるため、広く用いられている。 ラウドネスと異なる理由の一つは、フィルターが耳と同じように反応しないためである。 音の大きさを理解するために、まず必要なことは、以下に示す、人間の耳の周波数応答を表すいくつかの曲線を参照することである。 (
対数の測定
- なぜデシベルを使うのでしょうか。 短時間の暴露で永久的な損傷を引き起こす音圧と、（損傷を受けていない）耳が聞き取ることのできる限界の比率は、100 万以上です。 このような音域を扱うには対数単位が便利で、100万の対数は6なので、この比率は120dBの差を表している。 聴覚は本来、対数的に反応するものではありません。 (音が（短時間で）時間とともに指数関数的に増加または減少する場合にも、対数的な測定が有効です。 これは、比例利得または比例損失を含む多くのアプリケーションで起こります。）
dBA および dB(C) に使用されるフィルター
最も広く使用されているサウンド レベル フィルターは A スケールで、40 dB (1 kHz で) 等ラウドネス曲線の逆数にほぼ相当します。 このフィルタを使用すると、サウンドレベルメーターは、したがって、非常に高い周波数と非常に低い周波数に対する感度が低くなります。 このスケールで行われた測定値はdBAで表される。 Cスケールは数オクターブにわたってほとんど変化しないため、中程度から高い音圧レベルの主観的な測定にのみ適している。 このスケールでの測定値は、dB(C)で表される。 下図は、Aフィルタ（左）とCフィルタの応答で、1kHzに対する利得をdBで表しています。 (フィルタについては、RCフィルタ、積分器、微分器を参照してください)。
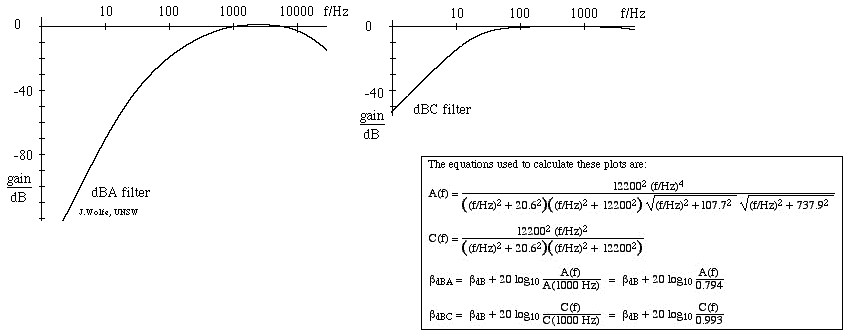
音楽音響と音声音響のサイトでは、サウンド スペクトルを dB でプロットしています。
dB(G) の測定では、1 ～ 20 Hz の周波数に高い重み付けをし、その他の周波数に低い重み付けをする狭帯域フィルタを使用します。
dB(G)の測定では、1～20Hzの周波数に高い重み付けをし、それ以外の周波数には低い重み付けをする狭帯域フィルタを使用します。 ISO 7196:1995
Loudness, phons and sones, hearing response curves
フォンは、耳の心理物理的に測定された周波数応答によってdBに関連付けられる単位です。 1 kHz では、フォンと dB の読みは、定義上、同じになります。 それ以外の周波数では、ボランティアがある周波数の信号の大きさを、1kHzの信号と同じ大きさだと判断するまで調整するよう求められた実験の結果によって、フォンスケールが決定される。 dBからフォンに変換するためには、このような結果をグラフにする必要がある。 このグラフは音の大きさに依存し、音が大きいと平坦になる。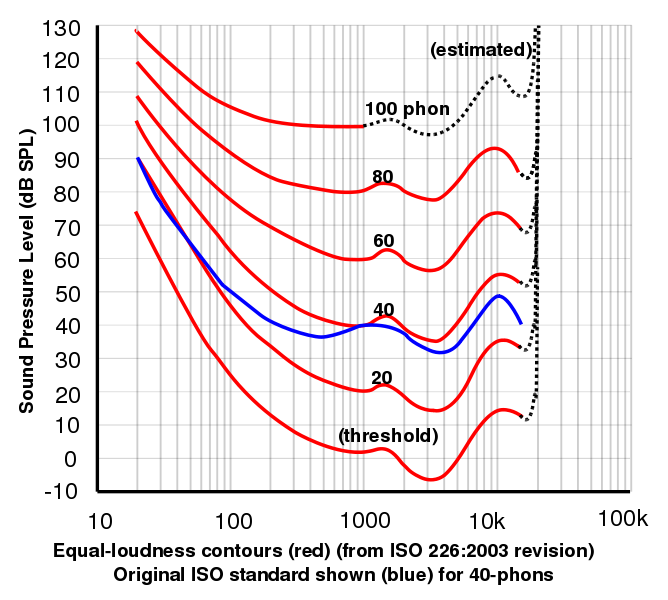 
この図は Lindosland の提供で、国際標準化機構の実験的に決めたカーブの 2003年のデータを示しています。 周波数の関数としての等ラウドネスのプロットは、Fletcher, H. and Munson, W.A. (1933) J.Acoust.Soc.Am. によるオリジナル作品にちなみ、一般に Fletcher-Munson 曲線と呼ばれることがよくあります。 6:59. 聴覚応答のサイトでは、独自のカーブを作成することができます。
音は、ボランティアが 2 倍の音量と判断するまで音を調整する心理物理学的測定から導き出されたものです。 これにより、知覚された音の大きさをフォンに関連付けることができます。 1 ソーンは 40 フォンに相当すると定義されています。 実験によると、40フォーン以上では、音量を10dB上げると、知覚される音量がおよそ2倍になることがわかった。 そのため、1ソーン＝40フォン、2ソーン＝50フォン、4ソーン＝60フォンなど、ソーンの定義にその近似値が使われている。
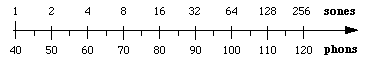
この関係から、ラウドネスと強さは乗則によって関係しており、音量の単位は (intensity)log 2 = (intensity)0.3 と比例することが示唆されます。
測定器で測定できる dB から、人が知覚するラウドネスに近似する sones に変換できたら素晴らしいと思いませんか? これは、音響学のハンドブックにあるような表を使って行われることがあります。 しかし、かなり粗い近似値でかまわないなら、Aの重み付け曲線は低音から中音までの人間の周波数応答に近似しているので、dB（A）は限られた低音域ではフォンスとほぼ同じになると言うことができます。 そうすると、前述したソーンとフォンの対数関係が使えることになる。
録音レベルとデシベル
オーディオ電子機器 (ミキシング コンソールなど) で録音または出力レベルを測定するメーターは、ほとんど常に AC 実効値電圧を記録します (AC と実効値について知るにはリンクを参照してください)。 ある抵抗 R に対して、電力 P は V2/R ですので、
電圧レベルの差 = 20 log (V2/V1) dB = 10 log (V22/V12) dB = 10 log (P2/P1) dB、または
絶対電圧レベル = 20 log (V/Vref)
ここで Vref は基準電圧とします。 では、基準電圧は何でしょうか。
当然選ぶべきレベルは1ボルト実効値で、この場合レベルはdBVと表記されます。 これは合理的ですし、最大レンジが1ボルトrms程度であることが多いアナログデジタルカードでは便利です。 したがって、信号のピークをクリップしないように、レベルを負のdBV（1ボルト以下）に保つことを忘れてはならないが、負になりすぎないようにしなければならない（そうすれば、信号はバックグラウンドノイズよりはるかに大きいままである）。
ときどき、dBm と表示されることがあります。 これは、1 ミリワットに対する電力のデシベルを意味し、今でもそうであることがあります。 しかし、歴史的な理由により、これは複雑です。 20世紀半ば、多くのオーディオラインの公称インピーダンスは600Ωでした。 インピーダンスが純粋に抵抗性であり、V2/600Ω=1mWとすると、V=0.775ボルトとなります。 つまり、600Ωの負荷を使用する場合、1mWのパワーは0dBmであり、0.775Vとなるので、このようにレベルメーターを校正するのである。 問題は、電圧を測定するレベルメータをこのように校正してしまうと、600Ωに接続していなくても0.775Vで0dBmと表示されてしまうため、非論理的かもしれませんが、dBmは0.775Vを基準にしたdBとなることがあります（私が子供の頃、電卓は高価だったので父の古い計算尺を使っていましたが、カーソル窓にはその計算をしやすいように0.775と書かれていました……）。
dBV または dBm をサウンド レベルの dB に変換するにはどうしたらよいでしょうか。 簡単な方法はありません。 電力を音響パワーにどのように変換するかに依存します。 電気信号が直接ラウドスピーカーに接続されている場合でも、変換はラウドスピーカーの効率とインピーダンスに依存します。 そしてもちろん、ミキシングデスクでdBVを測定する場所と、音場の中であなたの耳がある場所の間には、パワーアンプや、様々な音響的な複雑さがあるかもしれません。
強度、放射、および dB
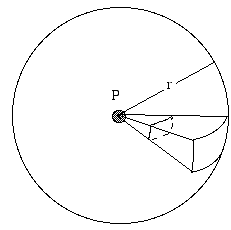
音量 (やラジオ信号レベルなど) は音源からの距離にどのように依存しますか?
すべての方向に等しく放射する音源を等方性と呼びます。 反射面から遠く離れた孤立した音源、たとえば空高く飛ぶ鳥の鳴き声を考えてみましょう。 音源を中心とした半径rの球を想像してください。 音源は全パワーPを連続的に出力しています。 この音響パワーは広がり、球体の表面を通過していきます。 音源が等方性であれば、強度Iは定義上、この表面上のどこでも同じになります。 強度Iは、単位面積あたりのパワーとして定義される。 球体の表面積は4πr2なので、表面の各平方メートルを通過するパワー（この例では音響パワー）は、定義により、次のようになります。
I = P/4πr2 です。
したがって、等方性音源の場合、強度は音源からの距離の 2 乗に反比例することがわかります。
I2/I1 = r12/r22。
しかし、強度は音圧の二乗に比例するので、同じように書くことができます。
p2/p1 = r1/r2。
したがって、距離を 2 倍にすれば、音圧は 2 倍に、強度は 4 倍になります。 言い換えれば、音のレベルを6dB下げるということです。
しかし、多くの音源は等方的ではないこと、特に波長が音源より小さい場合、または音源と同程度の大きさの場合、注意が必要です。 さらに、特に地面が近くにある場合や、屋内にいる場合は、反射が非常に重要であることがよくあります。
圧力、強度、および比インピーダンス
音波の場合、比音響インピーダンス z は、音波による圧力 p と平均粒子速度 u の比、z = p/u として定義されます。 Acoustic impedance, intensity and powerでは、実効音圧pと強度Iの関係を示しています：
I = p2/z
空気では、比音響インピーダンスzは420 kg.s-1.m-2 = 420 Pa.s.m-1 になります。 淡水の場合、水の比音響インピーダンスは1.48MPa.s.m-1である。 つまり、同じ圧力の水中の音波は、空気中の音波よりもはるかに小さな強度を持つことになる。
dBi と方向によって変化する放射
方向によって変化する放射は異方性と呼ばれます。 通信の多くの場合、等方性の放射は無駄です。受信者があなたのように比較的地上に近い場合、なぜ上向きにかなりの割合の電力を放出するのでしょうか。 波長の短い音（会話に重要な範囲のほとんどを含む）には、メガホンを使って声の異方性を高めることができます。 ラジオの場合、さまざまな設計により、送信と受信の両方でアンテナを高度に異方化することができます。
ですから、ある方向への放射（または受信）に関心がある場合、ある距離でその方向に測定した強度の比率を、等方性の放射体から同じ距離で測定した（または等方性の受信機で受信した）強度より高くしたいのです。 この比をdBで表すと、その放射体のdBi単位のゲインとなる。 この単位は主にアンテナの送受信に使われますが、音源や指向性マイクロホンにも使われることがあります。
例題
何人かの人が、計算で dB を使用する際の例題を求める書き込みをしています。 そこで…
- 他の条件がすべて同じ場合、10 W のアンプよりも 100 W のアンプで駆動されるスピーカーの方が (その線形範囲で) どれほど大きいか。
出力は10の倍数で、上で見たように10 dBです。 ここでいう「他のすべてが等しい」とは、周波数特性が等しい、同じ入力信号を使用する、などの意味です。 つまり、周波数依存性は同じであるはずです。 10dBは10フォーンに相当する。 ラウドネスを2倍と感じるには、10フォンの増加が必要です。 つまり、100Wのアンプで駆動したスピーカーは、10Wで駆動したスピーカーの2倍の音量となるわけですが、このとき、リニアの範囲内にとどまり、スピーカーを歪ませたり破壊したりしないことが前提です。 (100 W のアンプは 10 W のアンプの 2 倍の音を出します。)
- 私は、反射が無視できるような開けた場所で、小さな音源 (R よりはるかに小さいサイズ) から距離 R の位置に立っています。 今、私が距離 nR (n は数字で、nR は音源のサイズよりずっと大きい) に移動すると、新しいサウンドレベルはどうなるでしょうか?
まず、反射を無視することが非常に重要であることに注意してください。 この計算は部屋の中ではうまくいきません。壁からの反射（まとめて残響を発生させる）が計算をかなり難しくしているのです。 野外では、音の強さは1/r2（rは音源からの距離）に比例します。 (比例定数は地面の反射率に依存しますが、rが適度に大きければ計算上ほぼ相殺されるのでここでは関係ありません）。 つまり、rをRからnRに増加させると、強度はIからI/n 2に減少します。
強度 I 2 と I 1 の 2 つの信号間のデシベルの差は、上で
ΔL = 10 log (I2/I1) = 10 log ((I/n 2)/I) = 10 log (1/n 2) = -10 log (n 2) = -20 log n. として定義されます。
たとえば、n が 2 の場合 (つまり、2 倍の距離に行く場合)、強度は 4 分の 1 になり、サウンド レベルは L から (L – 6dB) に減少します。
- 理想的な静かな環境で、若者がラウドスピーカー (おそらくソフトスピーカー?) から発せられる 0 dB の 1 kHz 音を聞くことができる場合、音を 110 dB (危険な音量だが生存できるレベル) に上げるには、ラウドスピーカーの出力をどれだけ上げなければならないか。
パワー P2 と P1 の 2 つの信号のデシベルの差は、上で
ΔL = 10 log (P2/P1) dB と定義されているので、これらの 2 つの等しい量の 10 を上げると、以下のようになります。
10L/10 = P2/P1 ですから、
P2/P1 = 10110/10 = 1011 = 10億です。
これは、人間の耳が非常に大きなダイナミックレンジを持ち、おそらく目のダイナミックレンジよりも大きいことを実証しています。
- あるアンプは入力が 10 mV で、出力が 2 V です。 その電圧利得はdBで表すと何でしょうか。
電圧は圧力と同様に、電力や強度の表現で二乗されます。 (抵抗Rに散逸する電力はV2/Rです）そこで、慣習的にこう定義します。
gain = 20 log (Vout/Vin)
= 20 log (2V/10mV)
= 46 dB
（上記の音響のケースでは、dB で表される圧力比が電力比と同じであることがわかりました。 電圧利得の例では、アンプの電力利得が電圧利得と同じになる可能性が低いことは注目に値しますが、これはここで使用されている慣習によって定義されています。 電力は与えられた抵抗の電圧の二乗に比例します。 しかし、アンプの入力インピーダンスと出力インピーダンスは、多くの場合、かなり異なっている。 例えば、バッファアンプやエミッタフォロワは、電圧利得は1程度だが、電流利得は大きい)。
- 地球（太陽から8.3光年）と天王星（160光年）の放射照度（光強度）の差はdBで何ですか。
音と同様、等方性の光強度はr-2として減少するので、強度比は（160/8.3)2 = 20 log (160/8.3) = 26 dB.
労働衛生と安全
国や地方によって、職場での騒音暴露に関する法律は明らかに異なり、それは異なる熱意を持って施行されています。 そのような規制の多くは、8 時間のシフトにおける連続的な騒音への暴露の限度を 85 dB(A) と定めています。 3 dB増加するごとに、許容される暴露量は半分になります。 つまり、増幅された音楽が耳の近くで100 dB(A)を発生するナイトクラブで働く場合、許容される暴露時間は15分となります。 銃器や爆発物を使用する工具のようなインパルスノイズには制限があります。 (音源側（音楽のレベルを下げるなど）、音源と耳の間（コンサートでスピーカーから離れるなど）、耳元（耳栓や産業用聴覚保護具を着用するなど）での騒音暴露を低減する方法については、多くの文献でアドバイスがなされています。） オーストラリア・ニューサウスウェールズ州では、「Noise management and protection of hearing at work」が規範となっています（著者の住所はこちら）。
よくある質問
- 航空機の騒音はどのくらいですか? 電車ですか? 人が歌っている音？ 犬の鳴き声？ 電動工具？ この質問に対する答えは、かなり異なります。 どの程度離れているか、室内にいるかどうか、残響があるかどうか、特定の音源がどの程度強いか、そのスペクトルがどのようなものかによって、大きく異なります。 具体的な条件を示さずに数値を示すと、誤解を招く恐れがあります。 このページの他の部分は、信頼できるものであることを意図していますので、ここでは値を示さないことにします。
- どのように「デシベルを追加」するのか、つまり、レベル a をレベル b に追加すると、どのようなサウンド レベルになるのか。 音源がコヒーレントである場合 (通常、最終的に同じ音源に由来することを意味します)、複雑な干渉効果が発生する可能性があります。 音源が独立している場合、ほとんどの場合、強さを足してデシベルに変換することができます。 しかし、dB(A)単位で音の大きさが与えられた場合、強度に戻るのはそう簡単ではなく、音のスペクトルについて知っておく必要がある。 もし、音の周波数帯ごとの分布がわかれば、このリンクにあるアプレットを使うことができる。
- Some of the questions on our FAQ in music acoustics relate to decibels, including
- Why do the sounds of two musical instruments always reinforce, and never cancel out?
- How much does one more violin add to the sound level of a section of n violins?
- Does adding two equal sounds give an increase of 3 or 6 dB? Why?
- What is the loudest sound?
- Is there really no sound in space?
Related pages
- Measure your own hearing response
- Adding sound levels from incoherent sources
- What are interference beats and Tartini tones?
- FAQ in music acoustics
- Loudness and spectra: how spectral content and other features are related to loudness
- Formants: what are they? A discussion of the different meanings of this term
- Music acoustics home page
- Physclips: a multi-level, multimedia introduction to mechanics.
- A list of other educational web sites from this author.
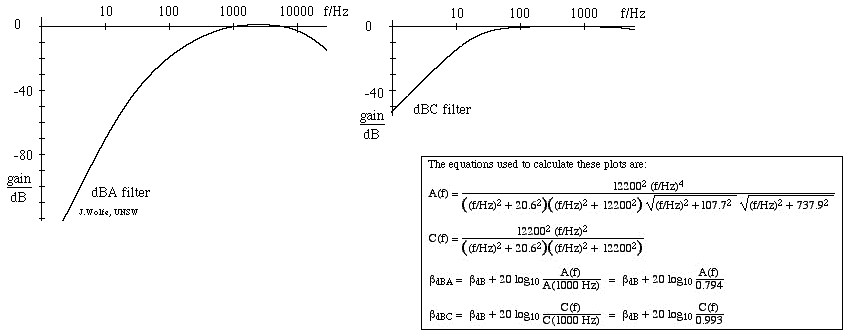
音楽音響と音声音響のサイトでは、サウンド スペクトルを dB でプロットしています。
dB(G) の測定では、1 ～ 20 Hz の周波数に高い重み付けをし、その他の周波数に低い重み付けをする狭帯域フィルタを使用します。
dB(G)の測定では、1～20Hzの周波数に高い重み付けをし、それ以外の周波数には低い重み付けをする狭帯域フィルタを使用します。 ISO 7196:1995
この図は Lindosland の提供で、国際標準化機構の実験的に決めたカーブの 2003年のデータを示しています。 周波数の関数としての等ラウドネスのプロットは、Fletcher, H. and Munson, W.A. (1933) J.Acoust.Soc.Am. によるオリジナル作品にちなみ、一般に Fletcher-Munson 曲線と呼ばれることがよくあります。 6:59. 聴覚応答のサイトでは、独自のカーブを作成することができます。
音は、ボランティアが 2 倍の音量と判断するまで音を調整する心理物理学的測定から導き出されたものです。 これにより、知覚された音の大きさをフォンに関連付けることができます。 1 ソーンは 40 フォンに相当すると定義されています。 実験によると、40フォーン以上では、音量を10dB上げると、知覚される音量がおよそ2倍になることがわかった。 そのため、1ソーン＝40フォン、2ソーン＝50フォン、4ソーン＝60フォンなど、ソーンの定義にその近似値が使われている。
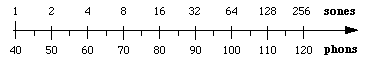
この関係から、ラウドネスと強さは乗則によって関係しており、音量の単位は (intensity)log 2 = (intensity)0.3 と比例することが示唆されます。
測定器で測定できる dB から、人が知覚するラウドネスに近似する sones に変換できたら素晴らしいと思いませんか? これは、音響学のハンドブックにあるような表を使って行われることがあります。 しかし、かなり粗い近似値でかまわないなら、Aの重み付け曲線は低音から中音までの人間の周波数応答に近似しているので、dB（A）は限られた低音域ではフォンスとほぼ同じになると言うことができます。 そうすると、前述したソーンとフォンの対数関係が使えることになる。
録音レベルとデシベル
- オーディオ電子機器 (ミキシング コンソールなど) で録音または出力レベルを測定するメーターは、ほとんど常に AC 実効値電圧を記録します (AC と実効値について知るにはリンクを参照してください)。 ある抵抗 R に対して、電力 P は V2/R ですので、
- 電圧レベルの差 = 20 log (V2/V1) dB = 10 log (V22/V12) dB = 10 log (P2/P1) dB、または
絶対電圧レベル = 20 log (V/Vref)
ここで Vref は基準電圧とします。 では、基準電圧は何でしょうか。
当然選ぶべきレベルは1ボルト実効値で、この場合レベルはdBVと表記されます。 これは合理的ですし、最大レンジが1ボルトrms程度であることが多いアナログデジタルカードでは便利です。 したがって、信号のピークをクリップしないように、レベルを負のdBV（1ボルト以下）に保つことを忘れてはならないが、負になりすぎないようにしなければならない（そうすれば、信号はバックグラウンドノイズよりはるかに大きいままである）。
ときどき、dBm と表示されることがあります。 これは、1 ミリワットに対する電力のデシベルを意味し、今でもそうであることがあります。 しかし、歴史的な理由により、これは複雑です。 20世紀半ば、多くのオーディオラインの公称インピーダンスは600Ωでした。 インピーダンスが純粋に抵抗性であり、V2/600Ω=1mWとすると、V=0.775ボルトとなります。 つまり、600Ωの負荷を使用する場合、1mWのパワーは0dBmであり、0.775Vとなるので、このようにレベルメーターを校正するのである。 問題は、電圧を測定するレベルメータをこのように校正してしまうと、600Ωに接続していなくても0.775Vで0dBmと表示されてしまうため、非論理的かもしれませんが、dBmは0.775Vを基準にしたdBとなることがあります（私が子供の頃、電卓は高価だったので父の古い計算尺を使っていましたが、カーソル窓にはその計算をしやすいように0.775と書かれていました……）。
dBV または dBm をサウンド レベルの dB に変換するにはどうしたらよいでしょうか。 簡単な方法はありません。 電力を音響パワーにどのように変換するかに依存します。 電気信号が直接ラウドスピーカーに接続されている場合でも、変換はラウドスピーカーの効率とインピーダンスに依存します。 そしてもちろん、ミキシングデスクでdBVを測定する場所と、音場の中であなたの耳がある場所の間には、パワーアンプや、様々な音響的な複雑さがあるかもしれません。
強度、放射、および dB
- 音量 (やラジオ信号レベルなど) は音源からの距離にどのように依存しますか?
すべての方向に等しく放射する音源を等方性と呼びます。 反射面から遠く離れた孤立した音源、たとえば空高く飛ぶ鳥の鳴き声を考えてみましょう。 音源を中心とした半径rの球を想像してください。 音源は全パワーPを連続的に出力しています。 この音響パワーは広がり、球体の表面を通過していきます。 音源が等方性であれば、強度Iは定義上、この表面上のどこでも同じになります。 強度Iは、単位面積あたりのパワーとして定義される。 球体の表面積は4πr2なので、表面の各平方メートルを通過するパワー（この例では音響パワー）は、定義により、次のようになります。
- I = P/4πr2 です。
したがって、等方性音源の場合、強度は音源からの距離の 2 乗に反比例することがわかります。
- I2/I1 = r12/r22。
しかし、強度は音圧の二乗に比例するので、同じように書くことができます。
- p2/p1 = r1/r2。
したがって、距離を 2 倍にすれば、音圧は 2 倍に、強度は 4 倍になります。 言い換えれば、音のレベルを6dB下げるということです。
しかし、多くの音源は等方的ではないこと、特に波長が音源より小さい場合、または音源と同程度の大きさの場合、注意が必要です。 さらに、特に地面が近くにある場合や、屋内にいる場合は、反射が非常に重要であることがよくあります。
圧力、強度、および比インピーダンス
- 音波の場合、比音響インピーダンス z は、音波による圧力 p と平均粒子速度 u の比、z = p/u として定義されます。 Acoustic impedance, intensity and powerでは、実効音圧pと強度Iの関係を示しています：
- I = p2/z
空気では、比音響インピーダンスzは420 kg.s-1.m-2 = 420 Pa.s.m-1 になります。 淡水の場合、水の比音響インピーダンスは1.48MPa.s.m-1である。 つまり、同じ圧力の水中の音波は、空気中の音波よりもはるかに小さな強度を持つことになる。
dBi と方向によって変化する放射
- 方向によって変化する放射は異方性と呼ばれます。 通信の多くの場合、等方性の放射は無駄です。受信者があなたのように比較的地上に近い場合、なぜ上向きにかなりの割合の電力を放出するのでしょうか。 波長の短い音（会話に重要な範囲のほとんどを含む）には、メガホンを使って声の異方性を高めることができます。 ラジオの場合、さまざまな設計により、送信と受信の両方でアンテナを高度に異方化することができます。
ですから、ある方向への放射（または受信）に関心がある場合、ある距離でその方向に測定した強度の比率を、等方性の放射体から同じ距離で測定した（または等方性の受信機で受信した）強度より高くしたいのです。 この比をdBで表すと、その放射体のdBi単位のゲインとなる。 この単位は主にアンテナの送受信に使われますが、音源や指向性マイクロホンにも使われることがあります。
例題
- 何人かの人が、計算で dB を使用する際の例題を求める書き込みをしています。 そこで…
- 他の条件がすべて同じ場合、10 W のアンプよりも 100 W のアンプで駆動されるスピーカーの方が (その線形範囲で) どれほど大きいか。
出力は10の倍数で、上で見たように10 dBです。 ここでいう「他のすべてが等しい」とは、周波数特性が等しい、同じ入力信号を使用する、などの意味です。 つまり、周波数依存性は同じであるはずです。 10dBは10フォーンに相当する。 ラウドネスを2倍と感じるには、10フォンの増加が必要です。 つまり、100Wのアンプで駆動したスピーカーは、10Wで駆動したスピーカーの2倍の音量となるわけですが、このとき、リニアの範囲内にとどまり、スピーカーを歪ませたり破壊したりしないことが前提です。 (100 W のアンプは 10 W のアンプの 2 倍の音を出します。)
- 私は、反射が無視できるような開けた場所で、小さな音源 (R よりはるかに小さいサイズ) から距離 R の位置に立っています。 今、私が距離 nR (n は数字で、nR は音源のサイズよりずっと大きい) に移動すると、新しいサウンドレベルはどうなるでしょうか?
まず、反射を無視することが非常に重要であることに注意してください。 この計算は部屋の中ではうまくいきません。壁からの反射（まとめて残響を発生させる）が計算をかなり難しくしているのです。 野外では、音の強さは1/r2（rは音源からの距離）に比例します。 (比例定数は地面の反射率に依存しますが、rが適度に大きければ計算上ほぼ相殺されるのでここでは関係ありません）。 つまり、rをRからnRに増加させると、強度はIからI/n 2に減少します。
強度 I 2 と I 1 の 2 つの信号間のデシベルの差は、上で
- ΔL = 10 log (I2/I1) = 10 log ((I/n 2)/I) = 10 log (1/n 2) = -10 log (n 2) = -20 log n. として定義されます。
たとえば、n が 2 の場合 (つまり、2 倍の距離に行く場合)、強度は 4 分の 1 になり、サウンド レベルは L から (L – 6dB) に減少します。
- 理想的な静かな環境で、若者がラウドスピーカー (おそらくソフトスピーカー?) から発せられる 0 dB の 1 kHz 音を聞くことができる場合、音を 110 dB (危険な音量だが生存できるレベル) に上げるには、ラウドスピーカーの出力をどれだけ上げなければならないか。
パワー P2 と P1 の 2 つの信号のデシベルの差は、上で
- ΔL = 10 log (P2/P1) dB と定義されているので、これらの 2 つの等しい量の 10 を上げると、以下のようになります。
10L/10 = P2/P1 ですから、
P2/P1 = 10110/10 = 1011 = 10億です。これは、人間の耳が非常に大きなダイナミックレンジを持ち、おそらく目のダイナミックレンジよりも大きいことを実証しています。
- あるアンプは入力が 10 mV で、出力が 2 V です。 その電圧利得はdBで表すと何でしょうか。
電圧は圧力と同様に、電力や強度の表現で二乗されます。 (抵抗Rに散逸する電力はV2/Rです）そこで、慣習的にこう定義します。
- gain = 20 log (Vout/Vin)
= 20 log (2V/10mV)
= 46 dB（上記の音響のケースでは、dB で表される圧力比が電力比と同じであることがわかりました。 電圧利得の例では、アンプの電力利得が電圧利得と同じになる可能性が低いことは注目に値しますが、これはここで使用されている慣習によって定義されています。 電力は与えられた抵抗の電圧の二乗に比例します。 しかし、アンプの入力インピーダンスと出力インピーダンスは、多くの場合、かなり異なっている。 例えば、バッファアンプやエミッタフォロワは、電圧利得は1程度だが、電流利得は大きい)。
- 地球（太陽から8.3光年）と天王星（160光年）の放射照度（光強度）の差はdBで何ですか。
音と同様、等方性の光強度はr-2として減少するので、強度比は（160/8.3)2 = 20 log (160/8.3) = 26 dB.
労働衛生と安全
国や地方によって、職場での騒音暴露に関する法律は明らかに異なり、それは異なる熱意を持って施行されています。 そのような規制の多くは、8 時間のシフトにおける連続的な騒音への暴露の限度を 85 dB(A) と定めています。 3 dB増加するごとに、許容される暴露量は半分になります。 つまり、増幅された音楽が耳の近くで100 dB(A)を発生するナイトクラブで働く場合、許容される暴露時間は15分となります。 銃器や爆発物を使用する工具のようなインパルスノイズには制限があります。 (音源側（音楽のレベルを下げるなど）、音源と耳の間（コンサートでスピーカーから離れるなど）、耳元（耳栓や産業用聴覚保護具を着用するなど）での騒音暴露を低減する方法については、多くの文献でアドバイスがなされています。） オーストラリア・ニューサウスウェールズ州では、「Noise management and protection of hearing at work」が規範となっています（著者の住所はこちら）。
よくある質問
- 航空機の騒音はどのくらいですか? 電車ですか? 人が歌っている音？ 犬の鳴き声？ 電動工具？ この質問に対する答えは、かなり異なります。 どの程度離れているか、室内にいるかどうか、残響があるかどうか、特定の音源がどの程度強いか、そのスペクトルがどのようなものかによって、大きく異なります。 具体的な条件を示さずに数値を示すと、誤解を招く恐れがあります。 このページの他の部分は、信頼できるものであることを意図していますので、ここでは値を示さないことにします。
- どのように「デシベルを追加」するのか、つまり、レベル a をレベル b に追加すると、どのようなサウンド レベルになるのか。 音源がコヒーレントである場合 (通常、最終的に同じ音源に由来することを意味します)、複雑な干渉効果が発生する可能性があります。 音源が独立している場合、ほとんどの場合、強さを足してデシベルに変換することができます。 しかし、dB(A)単位で音の大きさが与えられた場合、強度に戻るのはそう簡単ではなく、音のスペクトルについて知っておく必要がある。 もし、音の周波数帯ごとの分布がわかれば、このリンクにあるアプレットを使うことができる。
- Some of the questions on our FAQ in music acoustics relate to decibels, including
- Why do the sounds of two musical instruments always reinforce, and never cancel out?
- How much does one more violin add to the sound level of a section of n violins?
- Does adding two equal sounds give an increase of 3 or 6 dB? Why?
- What is the loudest sound?
- Is there really no sound in space?
Related pages
- Measure your own hearing response
- Adding sound levels from incoherent sources
- What are interference beats and Tartini tones?
- FAQ in music acoustics
- Loudness and spectra: how spectral content and other features are related to loudness
- Formants: what are they? A discussion of the different meanings of this term
- Music acoustics home page
- Physclips: a multi-level, multimedia introduction to mechanics.
- A list of other educational web sites from this author.