Solving the Königsberg Bridge Problem

This proof is accessible to ANYONE — no mathematics knowledge required! (perfect for if you are a bit bored and in isolation, like me right now!)

The Königsberg bridge problem shows the beauty of mathematics to transform the impossible to the obvious. It also gives an insight into the mind of the genius Leonhard Euler.

Stating the problem

Have a look at the map above.

It’s a diagram of the rivers and bridges of Königsberg. The areas A, B, C and D are bits of land, joined by the bridges, but otherwise cut off from each other by water.

A map of the city is below. どちらの図を見ても、どの土地の塊が他のどの土地の塊と、いくつの橋でつながっているかという重要な情報がわかります。

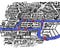
技術用語としては、これをグラフとして表現しています。 土地の塊が頂点で、橋が辺です。 しかし、それは重要ではありません。

問題は、すべての橋をちょうど 1 回通過するルートを見つけることが可能かどうかということです。 つまり、街を歩くとき、ルートはすべての橋を通りたいが、2回、3回と渡ることはできない…基本的に、以前と同じ橋の上にいることがわかったら、その道は無効となる。

解決策

土地の各ブロブを考えてみましょう。 各橋は 2 つの土地の塊に接続されています (これが橋の仕組みです)。

さて、有効な散歩がどのようなものか考えてみましょう。

散歩しながら、ある土地の塊にいるたびにメモ帳に記録します。 たとえば、街のいちばん南の端からスタートしたら、そのことをメモし（写真を撮る、お土産を買う…）、またそこにいたら、南の区間の集計を2つに増やします。

それぞれの土地の塊について、2つのケースがあります

(1)ここは、歩き始めても歩き終えてもいない街の区間です

(2)ここは、歩き始めるか、歩き終える、またはその両方です。

明らかに、2番目のタイプの街は、最大2区までしか存在しないことがわかります。

街には4つのセクションがあるので、私たちの散歩には、少なくとも2つのセクションがあり、それは私たちが終わっても始まってもいないことを意味します。

その区間に入るときはいつも橋を1本使い、離れるときはいつも別の橋を使います。 しかし、各セクターには奇数の橋がかかっているのです! これは矛盾です。

私たちが 1 回だけそのセクターに入った場合、その橋のうち 2 つしか使い切ることができません。

私たちがその区域に 1 回だけいる場合、その区域の橋の 2 つを使い切ることができます。私たちがその区域に 2 回いる場合、その橋の 4 つを使い切ります (または、3 つの橋しかない場合、橋が足りなくなります)。 3回入ったら、6本の橋が必要ですが、これは持てません。 つまり、スタート地点でもエンドポイントでもない街の区間に入ったり出たりするという条件は、区間ごとに接続する橋の数が奇数であるという事実と矛盾しています。