Marginale verdeling

Probabiliteitsverdelingen > Marginale verdeling

Wat is een marginale verdeling?

Bekijk de video of lees het artikel hieronder:

De technische definitie kan een beetje geestdodend zijn om naar te kijken:

Definitie van een marginale verdeling = Als X en Y discrete willekeurige variabelen zijn en f (x,y) is de waarde van
hun gezamenlijke kansverdeling op (x,y), dan zijn de functies gegeven door:
g(x) = Σy f (x,y) en h(y) = Σx f (x,y) de marginale verdelingen van respectievelijk X en Y zijn.

Als je goed bent met vergelijkingen, is dat waarschijnlijk alles wat je hoeft te weten. Het vertelt je hoe je een marginale verdeling vindt. Maar als die formule je hoofdpijn bezorgt (wat bij de meeste mensen het geval is!), kun je een frequentieverdelingstabel gebruiken om een marginale verdeling te vinden.

Een marginale verdeling dankt zijn naam aan het feit dat hij in de marges van een kansverdelingstabel verschijnt.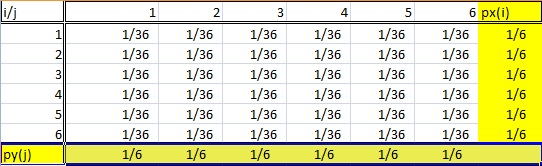

Zo eenvoudig is het natuurlijk niet. Je kunt niet zomaar naar een willekeurige frequentieverdelingstabel kijken en zeggen dat de laatste kolom (of rij) een “marginale verdeling” is. Marginale verdelingen volgen een paar regels:

• De verdeling moet afkomstig zijn van bivariate gegevens. Bivariaat is gewoon een andere manier om te zeggen “twee variabelen”, zoals X en Y. In de tabel hierboven zijn de willekeurige variabelen i en j afkomstig van de worp van twee dobbelstenen.
• Een marginale verdeling is wanneer je slechts geïnteresseerd bent in één van de willekeurige variabelen . Met andere woorden, of X of Y. Als je naar de bovenstaande kansentabel kijkt, staan de somkansen van één variabele in de onderste rij en de andere somkansen in de rechterkolom. Deze tabel heeft dus twee marginale verdelingen.

Verschil tussen marginale verdeling en voorwaardelijke verdeling.

Een voorwaardelijke verdeling is wanneer we alleen geïnteresseerd zijn in een bepaalde deelpopulatie van onze hele gegevensverzameling. In het voorbeeld van het gooien van de dobbelstenen kan dit zijn “een twee gooien” of “een zes gooien”. De afbeelding hieronder toont twee gemarkeerde subpopulaties (en dus twee voorwaardelijke verdelingen).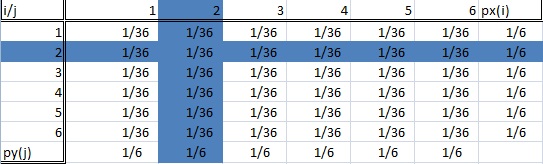

Hoe bereken je de marginale verdeling kans

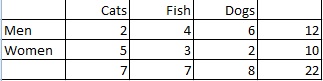
Voorbeeldvraag: Bereken de marginale verdeling van de voorkeur voor huisdieren onder mannen en vrouwen:
Oplossing:
Stap 1: Tel het totaal aantal mensen. In dit geval is het totaal gegeven in de rechterkolom (22 mensen).
Stap 2: Tel het aantal mensen dat de voorkeur geeft aan elk type huisdier en zet dan de verhouding om in een kans:
Mensen die de voorkeur geven aan katten: 7/22 = .32
Mensen die de voorkeur geven aan vissen: 7/22 = .32
Mensen die de voorkeur geven aan honden: 8/22 = .36
Tip: Je kunt je antwoord controleren door te kijken of de kansen allemaal opgeteld 1 zijn.

Voorbeeld vraag 2 (Wederzijds uitsluitende gebeurtenissen): Als P(A) = 0.20, P(b) = 0.70, en beide gebeurtenissen sluiten elkaar uit, zoek dan P(B’∩A), P(B’∩A’) en P(B∩A’).
Als je niet bekend bent met deze notatie, P(A’) betekent “niet A”, of het complement. P(B’∩A) betekent “het snijpunt van niet B en A”).

Antwoord:
Je zou de kansen individueel kunnen uitrekenen, maar met behulp van een tabel zijn ze veel eenvoudiger uit te rekenen.

Stap 1: Vul een frequentietabel in met de gegeven informatie. De totale kans moet gelijk zijn aan 1, dus die kun je ook bij de marges(totalen) optellen. Simpele optelling/algebra vult de marginale lege plekken in. Bijvoorbeeld, op de onderste rij 0.70 + x = 1.00 dus Het marginale totaal voor B’ moet 0.30 zijn.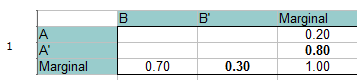

Stap 2: Voeg 0 toe voor het snijpunt van A en B, linksboven in de tabel. Dat kun je doen omdat A en B elkaar uitsluiten en niet samen kunnen voorkomen.

Stap 3: Vul de rest van de lege plekken in met eenvoudige optelling/algebra.

Uit de tabel aflezen (kijk naar de snijpunten van de twee genoemde kansen):
P(B’∩A) = 0,20
P(B’∩A’) = 0,10
P(B∩A’) = 0,70.

Voorbeeld vraag 3 (Onafhankelijke gebeurtenissen): Als P(A) = 0,20, P(b) = 0,70, en beide gebeurtenissen zijn onafhankelijk, vind dan P(B’∩A), P(B’∩A’) en P(B∩A’).

Antwoord: Deze keer zijn A en B onafhankelijk, dus de kans dat ze allebei op hetzelfde moment gebeuren is 0,14 (P(A)*P(B) = 0,20 * 0,70 = 0,14). Deze waarde komt in de linkerbovenhoek (snijpunt van A en B). Vul de rest van de tabel precies zo in als in de stappen hierboven.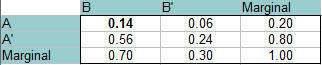

Lees de antwoorden uit de tabel (van de snijpunten van de twee kansen):
P(B’∩A): 0.06
P(B’∩A’): 0.24
P(B∩A’): 0.56.

Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, pp. 536 en 571, 2002.
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education

——————————————————————————

Heb je hulp nodig bij een huiswerk- of toetsvraag? Met Chegg Study kunt u stap-voor-stap oplossingen voor uw vragen krijgen van een expert op dit gebied. Uw eerste 30 minuten met een Chegg-leraar zijn gratis!