Solving the Königsberg Bridge Problem
This proof is accessible to ANYONE — no mathematics knowledge required! (perfect for if you are a bit bored and in isolation, like me right now!)
The Königsberg bridge problem shows the beauty of mathematics to transform the impossible to the obvious. It also gives an insight into the mind of the genius Leonhard Euler.

Stating the problem
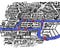
Have a look at the map above.
It’s a diagram of the rivers and bridges of Königsberg. The areas A, B, C and D are bits of land, joined by the bridges, but otherwise cut off from each other by water.
A map of the city is below. U kunt beide diagrammen bekijken – beide geven de belangrijkste informatie weer: welke klodders land zijn verbonden met welke andere klodders land, en door hoeveel bruggen.
In vakjargon stellen we dit voor als een grafiek. De klodders land zijn de hoekpunten, en de bruggen zijn de randen. Maar dat is niet belangrijk.
Het probleem is of het mogelijk is een route te vinden die over elke brug precies één keer gaat. Dat betekent dat we tijdens onze wandeling door de stad over elke brug willen gaan, maar dat we er niet twee keer overheen kunnen, of drie keer… In principe is het pad ongeldig als je op dezelfde brug komt als waar je eerder was. Als je klaar bent met je wandeling en er is een brug waar je niet overheen bent gelopen, dan was je route ongeldig.
De oplossing
Bekijk elke klodder land. Elke brug is verbonden met twee klodders land (zo werken bruggen). Elke landtong heeft toevallig een oneven aantal bruggen.
Nu gaan we eens kijken hoe een geldige wandeling eruit zou zien.
Tijdens je wandeling noteer je in een notitieblok elke keer dat je in een bepaalde landtong bent. Als u bijvoorbeeld in het zuidelijkste puntje van de stad begint, maakt u daar een aantekening van (neemt u een foto, koopt u een souvenir…) en als u daar weer komt, verhoogt u de teller voor de zuidelijke sector tot twee.
Voor elke klodder land zijn er twee gevallen
(1) dit is een stadsdeel waarin we noch onze wandeling beginnen, noch onze wandeling daar beëindigen
(2) dit is een stadsdeel waarin we ofwel onze wandeling beginnen, ofwel onze wandeling beëindigen, ofwel allebei.
Het is duidelijk dat er maximaal 2 stadsdelen van het tweede type zijn. We kunnen niet op twee plaatsen tegelijk beginnen, noch op twee plaatsen tegelijk eindigen.
Als er vier stadsdelen zijn, betekent dat, dat er in onze wandeling minstens twee stadsdelen zijn, waar we noch eindigen, noch beginnen. Laten we er een kiezen.
Telkens als we die sector binnengaan, gebruiken we een brug, en als we hem verlaten, gebruiken we een andere. Maar aan elke sector zit een oneven aantal bruggen vast! Dat is een tegenstrijdigheid. Om te zien waarom, herinner je je dat elke sector of 3 bruggen heeft, of dat er 5 bruggen aan vast zitten.
Als we één keer in de sector zijn, kunnen we maar twee van de bruggen opgebruiken. Als we er twee keer zijn, gebruiken we vier bruggen (of hebben we geen bruggen meer, als er maar drie bruggen waren). Als we er drie keer in zijn, hebben we 6 bruggen nodig, die we niet kunnen hebben. Dus de eis dat we zowel een sector van de stad binnengaan als verlaten die niet ons begin- of eindpunt is, is in tegenspraak met het feit dat het aantal verbindingsbruggen oneven is voor elke sector.