Soorten Interpolatie – Voor- en nadelen
Interpolatiemethoden
Interpolatie is het proces waarbij punten met bekende waarden of monsterpunten worden gebruikt om waarden op andere onbekende punten te schatten. Het kan worden gebruikt om onbekende waarden te voorspellen voor alle geografische puntgegevens, zoals hoogte, regenval, chemische concentraties, geluidsniveaus, enzovoort.
De beschikbare interpolatiemethoden worden hieronder opgesomd.
Inverse Distance Weighted (IDW)
De Inverse Distance Weighting interpolator gaat ervan uit dat elk invoerpunt een lokale invloed heeft die afneemt met de afstand. Hij weegt de punten dichter bij de verwerkingscel zwaarder dan die verder weg. Een gespecificeerd aantal punten, of alle punten binnen een gespecificeerde straal kunnen worden gebruikt om de outputwaarde van elke locatie te bepalen. Bij gebruik van deze methode wordt ervan uitgegaan dat de variabele die in kaart wordt gebracht, in invloed afneemt met de afstand vanaf de bemonsterde locatie.
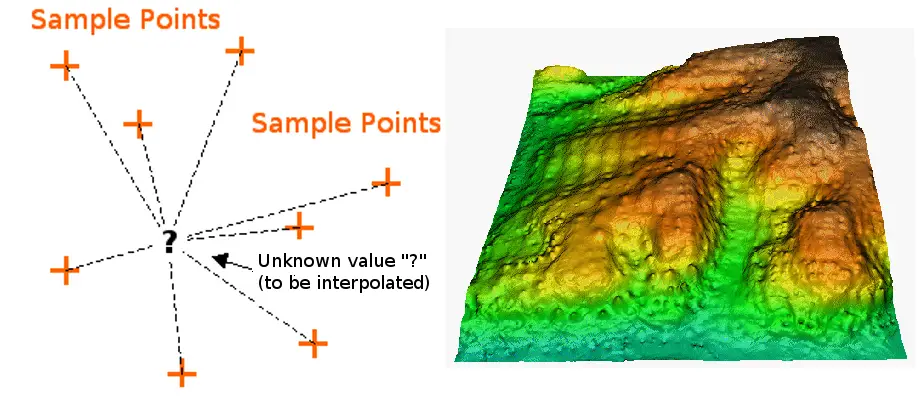
IDW Interpolatie; met dank aan: QGIS
Het IDW-algoritme (Inverse Distance Weighting) is in feite een interpolator voor voortschrijdend gemiddelde die gewoonlijk wordt toegepast op zeer variabele gegevens. Voor bepaalde soorten gegevens is het mogelijk terug te keren naar de verzamelplaats en een nieuwe waarde te registreren die statistisch verschilt van de oorspronkelijke meting, maar binnen de algemene trend voor het gebied ligt.
Het geïnterpoleerde oppervlak, geschat met behulp van een techniek van voortschrijdend gemiddelde, is kleiner dan de plaatselijke maximumwaarde en groter dan de plaatselijke minimumwaarde.

IDW Interpolated Surface; Met dank aan:ESRI
IDW interpolatie implementeert expliciet de aanname dat dingen die dicht bij elkaar liggen meer op elkaar lijken dan dingen die verder uit elkaar liggen. Om een waarde te voorspellen voor een ongemeten plaats, zal IDW de gemeten waarden rond de voorspellingsplaats gebruiken. De meetwaarden die het dichtst bij de voorspellocatie liggen, zullen meer invloed hebben op de voorspelde waarde dan de waarden die verder weg liggen. IDW gaat er dus van uit dat elk gemeten punt een lokale invloed heeft die afneemt met de afstand. De IDW-functie moet worden gebruikt wanneer de puntenverzameling dicht genoeg is om de omvang van de voor de analyse vereiste lokale oppervlaktevariatie vast te leggen. IDW bepaalt de celwaarden met behulp van een lineair gewogen combinatieverzameling van monsterpunten. De punten dichter bij de plaats van de voorspelling worden zwaarder gewogen dan die verder weg, vandaar de naam inverse distance weighted.
De IDW-techniek berekent een waarde voor elk rasterknooppunt door de omringende gegevenspunten te onderzoeken die binnen een door de gebruiker gedefinieerde zoekradius liggen. Sommige of alle datapunten kunnen worden gebruikt in het interpolatieproces. De knooppuntwaarde wordt berekend door het gemiddelde te nemen van de gewogen som van alle punten. Datapunten die steeds verder van het knooppunt afliggen hebben veel minder invloed op de berekende waarde dan datapunten die dichter bij het knooppunt liggen.
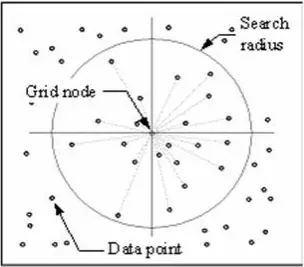
Om elk rasterknooppunt wordt een straal gegenereerd waaruit gegevenspunten worden geselecteerd die voor de berekening worden gebruikt. Options to control the use of IDW include power, search radius, fixed search radius, variable search radius and barrier.
Note: The optimal power (p) value is determined by minimizing the root mean square prediction error (RMSPE).
Advantages
- Can estimate extreme changes in terrain such as: Cliffs, Fault Lines.
- Dense evenly space points are well interpolated (flat areas with cliffs).
- Can increase or decrease amount of sample points to influence cell values.
Disadvantages
- Cannot estimate above maximum or below minimum values.
- Not very good for peaks or mountainous areas.
Natural Neighbour Inverse Distance Weighted (NNIDW)
Natural neighbor interpolation has many positive features, can be used for both interpolation and extrapolation, and generally works well with clustered scatter points. De basisvergelijking van natuurlijke buurinterpolatie, een andere methode met gewogen gemiddelden, is identiek aan die van IDW-interpolatie. Deze methode kan efficiënt omgaan met grote gegevenssets met invoerpunten. Bij gebruik van de Natural Neighbor methode bepalen de lokale coördinaten de mate van invloed die elk scatterpunt zal hebben op de outputcellen.
De Natural Neighbour methode is een geometrische schattingstechniek die gebruik maakt van natuurlijke buurtregio’s die rond elk punt in de dataset worden gegenereerd.
Net als IDW is deze interpolatiemethode een gewogen-gemiddelde interpolatiemethode. In plaats van de waarde van een geïnterpoleerd punt te vinden met behulp van alle invoerpunten, gewogen naar hun afstand, maakt natuurlijke bureninterpolatie een Delauney-triangulatie van de invoerpunten en selecteert de dichtstbijzijnde knooppunten die een convexe schil rond het interpolatiepunt vormen, waarna hun waarden worden gewogen naar evenredige oppervlakte. Deze methode is het meest geschikt wanneer de monstergegevenspunten ongelijkmatig verdeeld zijn. Het is een goede interpolatietechniek voor algemeen gebruik en heeft het voordeel dat u geen parameters zoals straal, aantal buren of gewichten hoeft op te geven.

Natuurlijke IDW: met dank aan: ESRI
Deze techniek is ontworpen om lokale minimum- en maximumwaarden in het puntenbestand te honoreren en kan worden ingesteld om overshoots van lokale hoge waarden en undershoots van lokale lage waarden te beperken. De methode maakt het dus mogelijk om nauwkeurige oppervlaktemodellen te maken van datasets die zeer dun verdeeld zijn of zeer lineair in ruimtelijke verdeling.
Voordelen
- Hanteert op efficiënte wijze grote aantallen monsterpunten.
Spline
Spline schat waarden met behulp van een wiskundige functie die de algehele kromming van het oppervlak minimaliseert, wat resulteert in een glad oppervlak dat precies door de invoerpunten loopt.

Spline: Met dank aan: ESRI
Conceptueel is het analoog aan het buigen van een vel rubber om door bekende punten te gaan terwijl de totale kromming van het oppervlak wordt geminimaliseerd. De methode past een wiskundige functie toe op een bepaald aantal dichtstbijzijnde invoerpunten terwijl ze door de monsterpunten gaat. Deze methode is het meest geschikt voor oppervlakken die licht variëren, zoals hoogteverschillen, grondwaterstanden of verontreinigingsconcentraties.
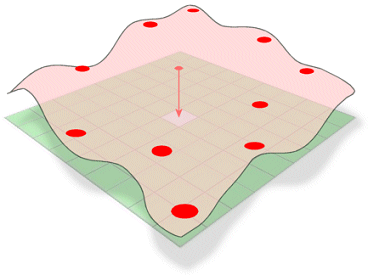
De Spline-methode voor interpolatie schat onbekende waarden door een oppervlak door bekende waarden te buigen.
Er zijn twee spline-methoden: geregulariseerde en spanningsmethode.
Een geregulariseerde methode creëert een glad, geleidelijk veranderend oppervlak met waarden die buiten het bereik van de steekproefgegevens kunnen liggen. De eerste afgeleide (helling), tweede afgeleide (snelheid van verandering in helling), en derde afgeleide (snelheid van verandering in de tweede afgeleide) worden opgenomen in de minimalisatieberekeningen.
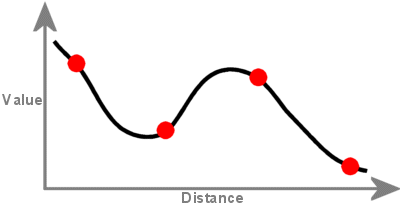
Een oppervlak dat is gemaakt met Spline-interpolatie gaat door elk monsterpunt heen en kan het waardebereik van de monsterpuntenset overschrijden.
Hoewel een Tension spline enkel eerste en tweede afgeleiden gebruikt, neemt het meer punten op in de Spline berekeningen, wat meestal gladdere oppervlakken oplevert maar de rekentijd verhoogt.
Deze methode trekt een oppervlak over de verkregen punten wat resulteert in een uitgerekt effect. Spline gebruikt gebogen lijnen (curvilinear Lines methode) om celwaarden te berekenen.
Het kiezen van een gewicht voor Spline Interpolaties
Geregulariseerde spline: Hoe hoger het gewicht, hoe gladder het oppervlak. Gewichten tussen 0 en 5 zijn geschikt. Typische waarden zijn 0, .001, .01, .1, en .5.
Tension spline: Hoe hoger het gewicht, hoe grover het oppervlak en hoe meer de waarden overeenkomen met het bereik van de steekproefgegevens. Gewichtswaarden moeten groter dan of gelijk aan nul zijn. Typical values are 0, 1, 5, and 10.
Advantages
- Useful for estimating above maximum and below minimum points.
- Creates a smooth surface effect.
Disadvantages
- Cliffs and fault lines are not well presented because of the smoothing effect.
- When the sample points are close together and have extreme differences in value, Spline interpolation doesn’t work as well. This is because Spline uses slope calculations (change over distance) to figure out the shape of the flexible rubber sheet.
Kriging
Kriging is a geostatistical interpolation technique that considers both the distance and the degree of variation between known data points when estimating values in unknown areas. A kriged estimate is a weighted linear combination of the known sample values around the point to be estimated.
Kriging-procedure die een geschat oppervlak genereert uit een verspreide verzameling punten met z-waarden. Kriging gaat ervan uit dat de afstand of richting tussen monsterpunten een ruimtelijke correlatie weerspiegelt die kan worden gebruikt om variatie in het oppervlak te verklaren. Het Kriging-gereedschap past een wiskundige functie toe op een gespecificeerd aantal punten, of alle punten binnen een gespecificeerde straal, om de outputwaarde voor elke locatie te bepalen. Kriging is een meerstappen-proces; het omvat verkennende statistische analyse van de gegevens, variogram-modellering, het creëren van het oppervlak, en (optioneel) het verkennen van een variantie-oppervlak. Kriging is het meest geschikt wanneer u weet dat er een ruimtelijk gecorreleerde afstand of richtingsafwijking in de gegevens zit. Het wordt vaak gebruikt in de bodemkunde en geologie.
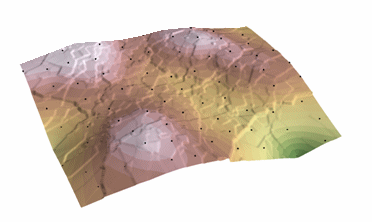
Kriging: Courtesy: ESRI
The predicted values are derived from the measure of relationship in samples using sophisticated weighted average technique. It uses a search radius that can be fixed or variable. The generated cell values can exceed value range of samples, and the surface does not pass through samples.
The Kriging Formula
Kriging is similar to IDW in that it weights the surrounding measured values to derive a prediction for an unmeasured location. The general formula for both interpolators is formed as a weighted sum of the data:
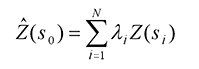
- where:
Z(si) = the measured value at the ith location
λi = an unknown weight for the measured value at the ith location
s0 = the prediction location
N = the number of measured values
In IDW, the weight, λi, depends solely on the distance to the prediction location. Bij de kriging-methode zijn de gewichten echter niet alleen gebaseerd op de afstand tussen de gemeten punten en de voorspellingslocatie, maar ook op de algemene ruimtelijke rangschikking van de gemeten punten. Om de ruimtelijke rangschikking in de gewichten te gebruiken, moet de ruimtelijke autocorrelatie worden gekwantificeerd. Bij gewone kriging hangt het gewicht, λi, dus af van een passend model voor de gemeten punten, de afstand tot de voorspellingslocatie, en de ruimtelijke relaties tussen de gemeten waarden rond de voorspellingslocatie. De volgende secties bespreken hoe de algemene kriging-formule wordt gebruikt om een kaart te maken van het voorspellingsoppervlak en een kaart van de nauwkeurigheid van de voorspellingen.
Typen Kriging
Ordinaire Kriging
Ordinaire kriging gaat uit van het model
Z(s) = µ + ε(s),
waarbij µ een onbekende constante is. Een van de belangrijkste vragen bij gewone kriging is of de aanname van een constant gemiddelde redelijk is. Sometimes there are good scientific reasons to reject this assumption. However, as a simple prediction method, it has remarkable flexibility.
Ordinary kriging can use either semivariograms or covariances, use transformations and remove trends, and allow for measurement error.
Simple Kriging
Simple kriging assumes the model
Z(s) = µ + ε(s),
where µ is a known constant.
Simple kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Universal Kriging
Universal kriging assumes the model
Z(s) = µ(s) + ε(s),
where µ(s) is some deterministic function.
Universal kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Indicator Kriging
Indicator kriging gaat uit van het model
I(s) = µ + ε(s),
waarbij µ een onbekende constante is en I(s) een binaire variabele. De creatie van binaire gegevens kan gebeuren door het gebruik van een drempel voor continue gegevens, of het kan zijn dat de waargenomen gegevens 0 of 1 zijn. U zou bijvoorbeeld een steekproef kunnen hebben die bestaat uit informatie over het feit of een punt al dan niet een bos of een niet-bos habitat is, waarbij de binaire variabele het lidmaatschap van een klasse aangeeft. Met behulp van binaire variabelen gaat indicator kriging op dezelfde manier te werk als gewone kriging.
Indicator kriging kan zowel semivariogrammen als covarianties gebruiken.
Probabiliteitskriging
Probabiliteitskriging gaat uit van het model
I(s) = I(Z(s) > ct) = µ1 + ε1(s)Z(s) = µ2 + ε2(s),
waarbij µ1 en µ2 onbekende constanten zijn en I(s) een binaire variabele is die wordt gecreëerd met behulp van een drempelindicator, I(Z(s) > ct). Merk op dat er nu twee soorten toevallige fouten zijn, ε1(s) en ε2(s), zodat er autocorrelatie is voor elk van hen en kruiscorrelatie tussen hen. Probability kriging streeft hetzelfde na als indicator kriging, maar het gebruikt cokriging in een poging om het beter te doen.
Probability kriging kan zowel semivariogrammen als covarianties, cross-covarianties en transformaties gebruiken, maar kan geen rekening houden met meetfouten.
style=”display:inline-block;width:468px;height:60px” data-ad-client=”ca-pub-7134201556760050″ data-ad-slot=”9271753327″>
Disjunctive Kriging
Disjunctive kriging gaat uit van het model
f(Z(s)) = µ1 + ε(s),
waarin µ1 een onbekende constante is en f(Z(s)) een willekeurige functie van Z(s) is. Merk op dat je f(Z(s)) = I(Z(s) > ct) kunt schrijven, dus indicator kriging is een speciaal geval van disjunctive kriging. In Geostatistical Analyst kunt u met disjunctive kriging zowel de waarde zelf als een indicator voorspellen.
In het algemeen probeert disjunctive kriging meer te doen dan gewone kriging. Hoewel de beloningen groter kunnen zijn, zijn de kosten dat ook. Disjunctive kriging requires the bivariate normality assumption and approximations to the functions fi(Z(si)); the assumptions are difficult to verify, and the solutions are mathematically and computationally complicated.
Disjunctive kriging can use either semivariograms or covariances and transformations, but it cannot allow for measurement error.
Advantages
- Directional influences can be accounted for: Soil Erosion, Siltation Flow, Lava Flow and Winds.
- Exceeds the minimum and maximum point values
Disadvantages
- Does not pass through any of the point values and causes interpolated values to be higher or lower then real values.
** Voor een diepgaand inzicht in de wiskundige benadering van Kriging klikt u op Kriging een Interpolatiemethode.
PointInterp
Een methode die lijkt op IDW, maar de PointInterp-functie biedt meer controle over de buurt van de steekproeven. De invloed van een bepaald sample op de geïnterpoleerde rastercelwaarde hangt af van of het samplepunt in de buurt van de cel ligt en hoe ver het van de geïnterpoleerde cel afligt. Punten buiten de buurt hebben geen invloed.

PointInterp; Courtesy: ESRI
De gewogen waarde van de punten binnen de buurt wordt berekend met behulp van een inverse afstandsgewogen interpolatie of inverse exponentiële afstandsinterpolatie. Deze methode interpoleert een raster met behulp van puntkenmerken, maar laat verschillende soorten buurten toe. Buurten kunnen de vorm hebben van cirkels, rechthoeken, onregelmatige veelhoeken, annulussen of wiggen.
Trend
Trend is een statistische methode die het oppervlak vindt dat past bij de monsterpunten met behulp van een kleinste-kwadraten regressiefit. Het past één polynomiale vergelijking op het gehele oppervlak. Dit resulteert in een oppervlak dat de variantie van het oppervlak ten opzichte van de invoerwaarden minimaliseert. Het oppervlak wordt zo geconstrueerd dat voor elk invoerpunt het totaal van de verschillen tussen de werkelijke waarden en de geschatte waarden (d.w.z. de variantie) zo klein mogelijk zal zijn.

Trend; Courtsey:ESRI
Het is een onnauwkeurige interpolator, en het resulterende oppervlak gaat zelden door de invoerpunten heen. Deze methode detecteert echter trends in de steekproefgegevens en is vergelijkbaar met natuurlijke verschijnselen die doorgaans vloeiend variëren.
Voordeel
- Trendvlakken zijn goed voor het identificeren van patronen op grove schaal in gegevens; het geïnterpoleerde oppervlak gaat zelden door de monsterpunten heen.
Topo to Raster
Door de hoogtewaarden voor een raster te interpoleren, legt de Topo to Raster-methode beperkingen op die zorgen voor een hydrologisch correct digitaal hoogtemodel dat een verbonden drainagestructuur bevat en de bergkammen en stromen correct weergeeft op basis van ingevoerde contourgegevens. De methode maakt gebruik van een iteratieve eindige-verschilinterpolatietechniek die de rekenefficiëntie van plaatselijke interpolatie optimaliseert zonder de oppervlaktecontinuïteit van globale interpolatie te verliezen. Het is speciaal ontworpen om intelligent te werken met contour-input.
Hieronder ziet u een voorbeeld van een oppervlak dat is geïnterpoleerd uit hoogtepunten, hoogtelijnen, stroomlijnen en meerpolygonen met behulp van Topo to Raster interpolatie.
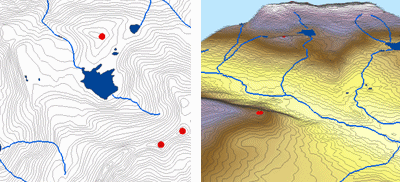
Topo naar raster; met dank aan: ESRI
Topo to Raster is een gespecialiseerd hulpmiddel voor het maken van hydrologisch correcte rasteroppervlakken uit vectorgegevens van terreincomponenten zoals hoogtelijnen, hoogtelijnen, stroomlijnen, meerpolygonen, zinkpunten, en studiegebiedgrenspolygonen.
Dichtheid
Dichtheidsgereedschappen (beschikbaar in ArcGIS) produceren een oppervlak dat weergeeft hoeveel of hoeveel van iets er zijn per oppervlakte-eenheid. Dichtheidsgereedschappen zijn nuttig om dichtheidsoppervlakken te maken om de verdeling van een populatie wilde dieren weer te geven op basis van een set waarnemingen, of de mate van verstedelijking van een gebied op basis van de dichtheid van wegen.

Density Raster; Courtest: ERSI
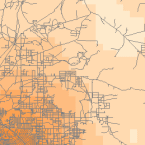
Density and Roads; Courtesy: ESRI
There are density tools for point and line features in ArcGIS.
Related Topics
- What is Interpolation ?
- Classification of Interpolation Techniques.
- Choosing the Right Interpolation Method