10.13: Avogadros hypotes och molär volym

admin

Avogadros hypotes och molär volym

Volym är ett tredje sätt att mäta mängden materia, efter antal artiklar och massa. Med vätskor och fasta ämnen varierar volymen mycket beroende på ämnets densitet. Detta beror på att fasta och flytande partiklar är packade tätt intill varandra med mycket litet utrymme mellan partiklarna. Gaser består dock till stor del av tomma utrymmen mellan själva gaspartiklarna (se figuren nedan).

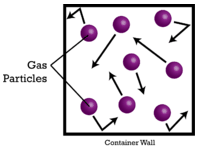
Figur \(\PageIndex{1}\): Gaspartiklar är mycket små jämfört med de stora mängderna tomt utrymme mellan dem.

År 1811 förklarade Amadeo Avogadro att volymerna av alla gaser lätt kan bestämmas. Avogadros hypotes säger att lika stora volymer av alla gaser vid samma temperatur och tryck innehåller lika många partiklar. Eftersom den totala volym som en gas upptar huvudsakligen består av det tomma utrymmet mellan partiklarna, är den faktiska storleken på själva partiklarna nästan försumbar. En given volym av en gas med små lätta partiklar som väte \(\left( \ce{H_2} \right)\) innehåller samma antal partiklar som samma volym av en tung gas med stora partiklar som svavelhexafluorid, \(\ce{SF_6}\).

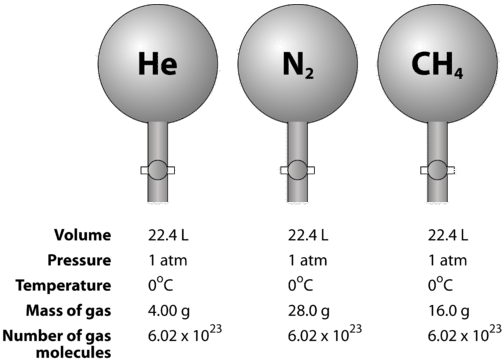
Gaser är komprimerbara, vilket innebär att när de sätts under högt tryck tvingas partiklarna närmare varandra. Detta minskar mängden tomrum och minskar gasens volym. Gasens volym påverkas också av temperaturen. När en gas värms upp rör sig molekylerna snabbare och gasen expanderar. På grund av variationen i gasvolym på grund av tryck- och temperaturförändringar måste jämförelsen av gasvolymer göras vid en standardtemperatur och ett standardtryck. Standardtemperatur och standardtryck (STP) definieras som \(0^\text{o} \text{C}\) \(\left( 273,15 \: \text{K} \right)\) och \(1 \: \text{atm}\) tryck. Den molära volymen av en gas är volymen av en mol av en gas vid STP. Vid STP upptar en mol (\( 6,02 \times 10^{23}\) representativa partiklar) av en gas en volym på \(22,4 \: \text{L}\) (figuren nedan).

Figur \(\(\PageIndex{2}\): En mol av en gas upptar \(22,4 \: \text{L}\) vid standardtemperatur och standardtryck (\(0^\text{o} \text{C}\) och \(1 \: \text{atm}\)).

Figuren nedan illustrerar hur molärvolymen kan ses när man jämför olika gaser. Prover av helium \(\left( \ce{He} \right)\), kväve \(\left( \ce{N_2} \right)\) och metan \(\left( \ce{CH_4} \right)\) är vid STP. Vardera innehåller 1 mol eller \(6,02 \ gånger 10^{23}\) partiklar. Massan för varje gas är dock annorlunda och motsvarar gasens molära massa: \(4.00 \: \text{g/mol}\) för \(\ce{He}\), \(28.0 \: \text{g/mol}\) för \(\ce{N_2}\), och \(16.0 \: \text{g/mol}\) för \(\ce{CH_4}\).

Figur \(\PageIndex{3}\): Avogadros hypotes säger att lika stora volymer av en gas vid samma temperatur och tryck innehåller lika många partiklar. Vid standardtemperatur och standardtryck upptar 1 mol av en gas \(22,4 \: \text{L}\).