dB: Vad är en decibel?

Ljudtryck, ljudnivå och dB. Ljud mäts vanligtvis med mikrofoner och de reagerar proportionellt mot ljudtrycket, p. Nu går effekten i en ljudvåg, allt annat lika, som kvadraten på trycket. (På samma sätt går den elektriska effekten i ett motstånd som kvadraten på spänningen). Logaritmen av x2 är bara 2 log x, så detta introducerar en faktor 2 när vi omvandlar tryckförhållanden till decibel. Skillnaden i ljudtrycksnivå mellan två ljud med p1 och p2 är därför:

20 log (p2/p1) dB = 10 log (p22/p12) dB = 10 log (P2/P1) dB (hela tiden är loggen till bas 10).

Vad händer när man halverar ljudeffekten? Logvärdet för 2 är 0,3010, så logvärdet för 1/2 är -0,3, med god approximation. Om du halverar effekten minskar du alltså effekten och ljudnivån med 3 dB. Om du halverar den igen (till 1/4 av den ursprungliga effekten) minskar du ljudnivån med ytterligare 3 dB. Om du fortsätter att halvera effekten får du dessa förhållanden.

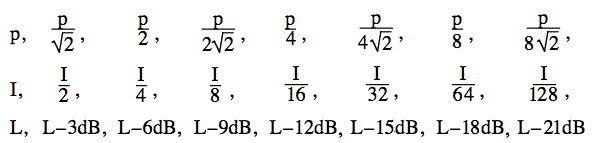
Vad händer om jag lägger till två identiska ljud? Fördubblar jag intensiteten (ökning med 3 dB)? Eller fördubblar jag trycket (ökning med 6 dB)? Denna ofta ställda fråga är lite subtil, så den diskuteras här i vår FAQ.

Ljudfiler för att visa storleken på en decibel

Vi såg ovan att en halvering av effekten minskar ljudtrycket med √2 och ljudnivån med 3 dB. Det är vad vi har gjort i den första grafiken och ljudfilen nedan.

Det första ljudprovet är vitt brus (en blandning av ett brett spektrum av hörbara frekvenser, analogt med vitt ljus som är en blandning av alla synliga frekvenser). Det andra provet är samma brus, med spänningen reducerad med en faktor √2. Nu är 1/√2 ungefär 0,7, så -3 dB motsvarar en minskning av spänningen eller trycket till 70 % av dess ursprungliga värde. Den gröna linjen visar spänningen som en funktion av tiden. Den röda linjen visar en kontinuerlig exponentiell minskning med tiden. Observera att spänningen sjunker med 50 % för varje andra provtagning. Observera också att en fördubbling av spänningen inte gör någon större skillnad för ljudstyrkan. Vi kommer att diskutera detta vidare nedan, men det är en nyttig sak att komma ihåg när man väljer utrustning för ljudåtergivning. Ljudfiler och animation av John Tann och George Hatsidimitris.

Hur stor är en decibel? I nästa serie minskas de på varandra följande proverna med bara en decibel.

En decibel är av samma storleksordning som Just Noticeable Difference (JND) för ljudnivå. När du lyssnar på dessa filer kommer du att märka att den sista är tystare än den första, men det är inte lika tydligt för örat att den andra i ett par är tystare än sin föregångare. 10*log10(1,26) = 1, så för att öka ljudnivån med 1 dB måste effekten ökas med 26 % eller spänningen med 12 %.

Vad händer om skillnaden är mindre än en decibel? Ljudnivåer anges sällan med decimaler. Anledningen är att ljudnivåer som skiljer sig med mindre än 1 dB är svåra att särskilja, vilket nästa exempel visar. (Detta gör dB till en praktisk storleksenhet.)

0,3 dB steg. Du kanske märker att det sista är tystare än det första, men det är svårt att märka skillnaden mellan på varandra följande par. 10*log10(1,07) = 0,3, så för att öka ljudnivån med 0,3 dB måste effekten ökas med 7 % eller spänningen med 3,5 %.

Standardiserade referensnivåer. (”absolut” ljudnivå)

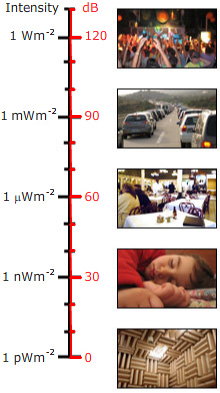Vi sa ovan att decibel är ett förhållande. Så när den används för att ange ljudnivån för ett enskilt ljud i stället för ett förhållande måste en referensnivå väljas. För ljudtrycksnivå brukar referensnivån (för luft) väljas som pref = 20 mikropascal (20 μPa), eller 0,02 mPa. Detta är mycket lågt: det är 2 tio miljarddelar av en atmosfär. Detta är dock ungefär gränsen för det mänskliga örats känslighet i dess känsliga frekvensområde. (Vanligtvis finns denna känslighet endast hos ganska unga människor eller hos människor som inte har utsatts för hög musik eller andra höga ljud. Personliga musiksystem med in-ear-högtalare kan ge mycket höga ljudnivåer i örat och anses av vissa vara orsaken till en stor del av hörselnedsättningen hos unga vuxna i vissa länder).

Så om du läser om en ljudtrycksnivå på 86 dB betyder det att

20 log (p2/pref) = 86 dB

där pref är ljudtrycket för referensnivån och p2 ljudtrycket för ljudet i fråga. Dela båda sidorna med 20:

log (p2/pref) = 4,3

p2/pref = 104,3

4 är log av 10 tusen, 0,3 är log av 2, så detta ljud har ett ljudtryck som är 20 tusen gånger högre än referensnivåns (p2/pref = 20 000) eller en intensitet 400 miljoner gånger referensintensiteten. 86 dB är ett högt ljud men inte farligt – förutsatt att exponeringen är kortvarig.

Vad betyder 0 dB? Denna nivå uppstår när den uppmätta intensiteten är lika med referensnivån, dvs. det är den ljudnivå som motsvarar 0,02 mPa. I detta fall har vi

ljudnivå = 20 log (pmätt/referens) = 20 log 1 = 0 dB

Kom ihåg att decibel mäter ett förhållande. 0 dB inträffar när man tar logaritmen av ett förhållande på 1 (log 1 = 0). Så 0 dB betyder inte att det inte finns något ljud, det betyder en ljudnivå där ljudtrycket är lika med referensnivån. Detta är ett litet tryck, men inte noll. Det är också möjligt att ha negativa ljudnivåer: – 20 dB skulle innebära ett ljud med ett tryck som är 10 gånger mindre än referenstrycket, dvs. 2 μPa.

Inte alla ljudtryck är lika höga. Detta beror på att det mänskliga örat inte reagerar lika på alla frekvenser: vi är mycket känsligare för ljud i frekvensområdet cirka 1 kHz till 7 kHz (1 000 till 7 000 vibrationer per sekund) än för mycket låg- eller högfrekventa ljud. Av denna anledning är ljudmätare vanligtvis utrustade med ett filter vars frekvensrespons är lite som det mänskliga örats. (Mer om dessa filter nedan.) Om ”A-viktningsfiltret” används anges ljudtrycksnivån i enheterna dB(A) eller dBA. Ljudtrycksnivån på dBA-skalan är lätt att mäta och används därför ofta. En anledning till att den skiljer sig från ljudstyrka är att filtret inte reagerar på samma sätt som örat. För att förstå hur högt ett ljud är, måste man först konsultera några kurvor som representerar det mänskliga örats frekvensrespons, som ges nedan. (Alternativt kan du mäta ditt eget hörselrespons.) Ett annat skäl är att det mänskliga hörseln inte är logaritmisk.

Logaritmiska mått

Varför använder vi decibel? Öronen kan höra ett mycket stort antal ljud: förhållandet mellan det ljudtryck som orsakar permanenta skador vid kortvarig exponering och den gräns som (oskadade) öron kan höra är mer än en miljon. För att hantera ett sådant intervall är logaritmiska enheter användbara: logaritmen av en miljon är 6, så detta förhållande motsvarar en skillnad på 120 dB. Hörseln är inte logaritmisk till sin natur. (Logaritmiska mått är också användbara när ett ljud (kortvarigt) ökar eller minskar exponentiellt över tiden. Detta sker i många tillämpningar som involverar proportionell förstärkning eller proportionell förlust.)

De filter som används för dBA och dB(C)

Det mest använda ljudnivåfiltret är A-skalan, som grovt sett motsvarar ungefär den omvända delen av 40 dB (vid 1 kHz) jämnhöjdskurvan. Genom att använda detta filter är ljudnivåmätaren alltså mindre känslig för mycket höga och mycket låga frekvenser. Mätningar som görs på denna skala uttrycks i dBA. C-skalan varierar lite över flera oktaver och är därför lämplig för subjektiva mätningar endast för måttliga till höga ljudnivåer. Mätningar på denna skala uttrycks som dB(C). Det finns också en (sällan använd) viktningsskala B, som ligger mellan A och C. Figuren nedan visar responsen hos A-filtret (till vänster) och C-filtret, med förstärkningar i dB angivna med avseende på 1 kHz. (För en introduktion till filter, se RC-filter, integratorer och differentiatorer).



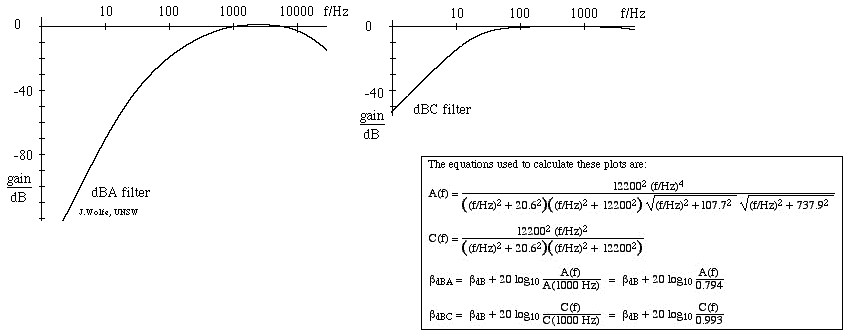
På sidorna för musikakustik och talakustik plottar vi ljudspektra i dB. Anledningen till denna vanliga praxis är att intervallet av uppmätta ljudtryck är stort.

BdB(G)-mätningar använder ett smalbandigt filter som ger hög vikt åt frekvenser mellan 1 och 20 Hz och låg vikt åt andra. Det ger därför stora värden för ljud och infraljud som inte lätt kan höras. ISO 7196:1995

Ljudstyrka, phon och soner, hörselresponskurvor

Phon är en enhet som är relaterad till dB genom örats psykofysiskt uppmätta frekvensrespons. Vid 1 kHz är avläsningar i phon och dB per definition lika. För alla andra frekvenser bestäms phonskalan av resultaten av experiment där frivilliga ombads att justera ljudstyrkan hos en signal vid en viss frekvens tills de bedömde att dess ljudstyrka var lika stor som hos en 1 kHz-signal. För att konvertera från dB till phonskala behöver du en graf över sådana resultat. En sådan graf beror på ljudnivån: den blir plattare vid höga ljudnivåer.

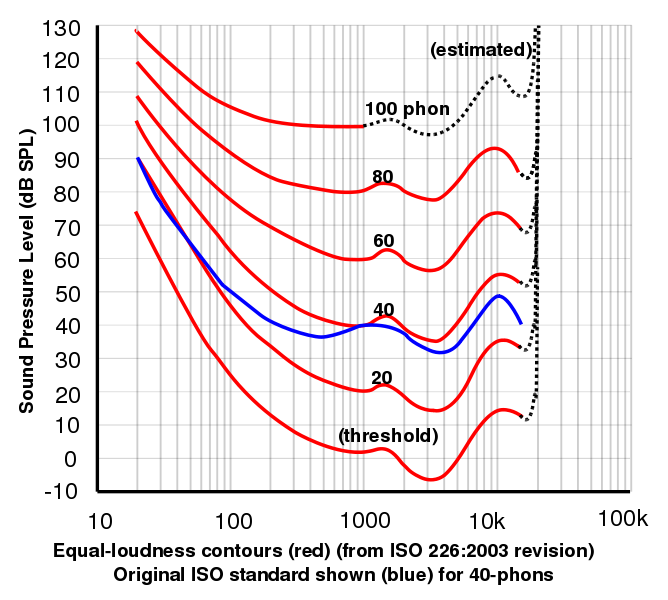
Denna graf, som är en artighet av Lindosland, visar 2003 års data från Internationella standardiseringsorganisationen för kurvor för lika hög ljudstyrka som fastställts experimentellt. Plottar med lika hög ljudstyrka som en funktion av frekvensen kallas ofta generiskt för Fletcher-Munson-kurvor efter det ursprungliga arbetet av Fletcher, H. och Munson, W.A. (1933) J.Acoust.Soc.Am. 6:59. Du kan göra dina egna kurvor med hjälp av vår webbplats för hörselrespons.

Sonen härrör från psykofysiska mätningar där frivilliga försökspersoner anpassar ljud tills de bedömer att de är dubbelt så högljudda. Detta gör det möjligt att relatera upplevd ljudstyrka till sone. En sone definieras som lika med 40 phon. Experimentellt har man funnit att över 40 phon motsvarar en ökning av ljudnivån med 10 dB ungefär en fördubbling av den upplevda ljudstyrkan. Denna approximation används alltså i definitionen av sone: 1 sone = 40 phon, 2 sone = 50 phon, 4 sone = 60 phon osv.



Detta förhållande innebär att ljudstyrka och intensitet hänger ihop med en potenslag: Ljudstyrka i sone är proportionell mot (intensitet)log 2 = (intensitet)0,3.

Vore det inte fantastiskt att kunna konvertera från dB (som kan mätas med ett instrument) till sones (som approximerar ljudstyrka som uppfattas av människor)? Detta görs ibland med hjälp av tabeller som man kan hitta i handböcker om akustik. Om man inte har något emot en ganska grov approximation kan man dock säga att A-viktkurvan approximerar människans frekvensrespons vid låga till måttliga ljudnivåer, så dB(A) är mycket ungefär detsamma som soner, över ett begränsat intervall av låga nivåer. Då kan man använda det logaritmiska förhållandet mellan sones och phons som beskrivs ovan.

Inspelningsnivå och decibel

Mätare som mäter inspelnings- eller utgångsnivå på ljudelektronisk utrustning (mixerbord etc.) registrerar nästan alltid AC rms-spänningen (se länkar för att ta reda på mer om AC och rms). För ett givet motstånd R är effekten P V2/R, så
skillnaden i spänningsnivå = 20 log (V2/V1) dB = 10 log (V22/V12) dB = 10 log (P2/P1) dB, eller

absolut spänningsnivå = 20 log (V/Vref)

där Vref är en referensspänning. Vad är då referensspänningen?

Den självklara nivån att välja är en volt rms, och i det här fallet skrivs nivån som dBV. Detta är rationellt, och även praktiskt med analog-digitala kort vars maximala intervall ofta är ungefär en volt rms. Man måste alltså komma ihåg att hålla nivån i negativ dBV (mindre än en volt) för att undvika att signalens toppar klipps av, men inte för negativ (så att signalen fortfarande är mycket större än bakgrundsbruset).

Ibland ser man dBm. Detta brukade betyda decibel av elektrisk effekt, med avseende på en milliwatt, och gör det ibland fortfarande. Det är dock komplicerat av historiska skäl. I mitten av 1900-talet hade många ljudledningar en nominell impedans på 600 Ω. Om impedansen är rent resistiv och om man ställer in V2/600 Ω = 1 mW får man V = 0,775 volt. Om du använde en belastning på 600 Ω var 1 mW effekt 0 dBm, vilket var 0,775 V, så du kalibrerade dina nivåmätare på detta sätt. Problemet uppstod därför att när en nivåmätare som mäter spänning kalibreras på detta sätt kommer den att avläsa 0 dBm vid 0,775 V även om den inte är ansluten till 600 Ω. Så, kanske ologiskt nog, kommer dBm ibland att betyda dB med avseende på 0,775 V. (När jag var pojke var miniräknare dyra, så jag använde pappas gamla skjutmåttstock, som hade faktorn 0,775 markerad i markörfönstret för att underlätta sådana beräkningar).

Hur konverterar man dBV eller dBm till dB ljudnivå? Det finns inget enkelt sätt. Det beror på hur man omvandlar den elektriska effekten till ljudeffekt. Även om din elektriska signal ansluts direkt till en högtalare beror omvandlingen på högtalarens effektivitet och impedans. Och naturligtvis kan det finnas en effektförstärkare och olika akustiska komplikationer mellan den plats där du mäter dBV på mixerbordet och den plats där dina öron befinner sig i ljudfältet.

Intensitet, strålning och dB

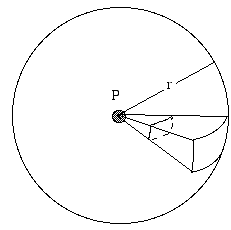
Hur beror ljudnivån (eller radiosignalnivån osv.) på avståndet från källan?

En källa som avger strålning lika mycket i alla riktningar kallas isotropisk. Tänk på en isolerad ljudkälla, långt från alla reflekterande ytor – kanske en fågel som sjunger högt upp i luften. Tänk dig en sfär med radie r, centrerad på källan. Ljudkällan avger kontinuerligt en total effekt P. Denna ljudeffekt sprids ut och passerar genom sfärens yta. Om källan är isotropisk är intensiteten I per definition densamma överallt på denna yta. Intensiteten I definieras som effekten per ytenhet. Sfärens yta är 4πr2, så den effekt (i vårt exempel, ljudeffekten) som passerar genom varje kvadratmeter av ytan är per definition:

I = P/4πr2.

Så ser vi att för en isotropisk källa är intensiteten omvänt proportionell mot kvadraten på avståndet från källan:

I2/I1 = r12/r22.

Men intensiteten är proportionell mot kvadraten på ljudtrycket, så vi kan också skriva:

p2/p1 = r1/r2.

Om vi fördubblar avståndet minskar vi alltså ljudtrycket med en faktor 2 och intensiteten med en faktor 4: med andra ord minskar vi ljudnivån med 6 dB. Om vi ökar r med en faktor 10 minskar vi ljudnivån med 20 dB osv.

Var dock uppmärksam på att många källor inte är isotropa, särskilt om våglängden är mindre än, eller av en storlek jämförbar med källan. Vidare är reflektioner ofta ganska viktiga, särskilt om marken är nära, eller om du befinner dig inomhus.

Tryck, intensitet och specifik impedans

För akustiska vågor definieras den specifika akustiska impedansen z som förhållandet mellan det akustiska trycket p och den genomsnittliga partikelhastigheten u, på grund av ljudet ave, z = p/u . I Akustisk impedans, intensitet och effekt visar vi hur man relaterar RMS akustiskt tryck p och intensitet I:
I = p2/z

För luft är den specifika akustiska impedansen z 420 kg.s-1.m-2 = 420 Pa.s.m-1. För (söt) vatten är den specifika akustiska impedansen för vatten 1,48 MPa.s.m-1. En ljudvåg i vatten med samma tryck har alltså en mycket lägre intensitet än en ljudvåg i luft.

dBi och strålning som varierar med riktning

Strålning som varierar i riktning kallas anisotrop. I många fall inom kommunikation är isotropisk strålning slösaktig: varför sända ut en betydande del av effekten uppåt om mottagaren, som du, befinner sig relativt nära marknivå. När det gäller ljud med kort våglängd (inklusive det mesta av det viktiga området för tal) kan en megafon hjälpa till att göra din röst mer anisotropisk. När det gäller radio finns det ett brett utbud av konstruktioner som gör att antennerna kan vara mycket anisotropa både för sändning och mottagning.

När man är intresserad av emission i (eller mottagning från) en viss riktning vill man alltså att förhållandet mellan intensiteten som mäts i den riktningen, på ett givet avstånd, ska vara högre än den som mäts på samma avstånd från en isotropisk strålare (eller tas emot av en isotropisk mottagare). Detta förhållande kallas förstärkning; uttrycka förhållandet i dB och du får förstärkningen i dBi för den radiatorn. Denna enhet används huvudsakligen för antenner, antingen för sändning eller mottagning, men den används ibland för ljudkällor och riktade mikrofoner.

Exempelproblem

Några personer har skrivit och bett om exempel på hur man använder dB i beräkningar. Så…
• Hur mycket högre är en högtalare som drivs (i sitt linjära område) av en förstärkare på 100 W än av en förstärkare på 10 W, om allt annat är lika?

  De olika effekterna skiljer sig åt med en faktor tio, vilket, som vi såg ovan, är 10 dB. Allt annat lika innebär här att frekvensresponserna är lika och att samma ingångssignal används osv. Så frekvensberoendet bör vara detsamma. 10 dB motsvarar 10 phon. För att få en upplevd fördubbling av ljudstyrkan krävs en ökning med 10 phon. Så högtalaren som drivs av förstärkaren på 100 W är dubbelt så högljudd som när den drivs av förstärkaren på 10 W, förutsatt att man håller sig inom det linjära området och inte förvränger eller förstör högtalaren. (Förstärkaren på 100 W producerar dubbelt så många soner som förstärkaren på 10 W.)

• Jag står på ett avstånd R från en liten ljudkälla (storlek mycket mindre än R), i marknivå ute i det fria där reflektioner kan försummas. Ljudnivån är L. Om jag nu flyttar mig till ett avstånd nR (n är ett tal och nR är fortfarande mycket större än källans storlek), vad blir då den nya ljudnivån?

  Först bör man notera att det är mycket viktigt att försumma reflektioner. Denna beräkning kommer inte att fungera inne i ett rum, där reflektioner från väggen (som tillsammans producerar efterklang) gör beräkningen ganska svår. Ute i det fria är ljudintensiteten proportionell mot 1/r2, där r är avståndet från källan. (Proportionalitetskonstanten beror på hur väl marken reflekterar, och berör oss inte här, eftersom den i stort sett kommer att utplånas i beräkningen, förutsatt att r är rimligt stor). Om vi ökar r från R till nR minskar vi alltså intensiteten från I till I/n 2.

  Skillnaden i decibel mellan de två signalerna med intensiteten I 2 och I 1 definieras ovan till

  ΔL = 10 log (I2/I1) = 10 log ((I/n 2)/I) = 10 log (1/n 2) = -10 log (n 2) = -20 log n.

  Till exempel, om n är 2 (dvs. om vi går dubbelt så långt bort) minskar intensiteten med en faktor fyra och ljudnivån sjunker från L till (L – 6dB).

• Om en ung person under idealiska tysta förhållanden kan höra en ton på 1 kHz vid 0 dB som sänds ut av en högtalare (kanske en mjuk högtalare?), med hur mycket måste högtalarens effekt ökas för att höja ljudet till 110 dB (en farligt hög men överlevnadsbar nivå)?

  Skillnaden i decibel mellan de två signalerna med effekten P2 och P1 definieras ovan som

  ΔL = 10 log (P2/P1) dB så, genom att höja 10 till potensen av dessa två lika stora mängder:
  10L/10 = P2/P1 så:
  P2/P1 = 10110/10 = 1011 = hundra tusen miljoner.

  Vilket är ett bevis på att det mänskliga örat har ett anmärkningsvärt stort dynamiskt omfång, kanske större än ögats.

• En förstärkare har en ingång på 10 mV och en utgång på 2 V. Vad är dess spänningsförstärkning i dB?

  Spänning, liksom tryck, förekommer i kvadrat i uttryck för effekt eller intensitet. (Den uteblivna effekten i ett motstånd R är V2/R.) Så enligt konvention definierar vi:

  förstärkning = 20 log (Vout/Vin)
  = 20 log (2V/10mV)
  = 46 dB

  (I de akustiska fallen ovan såg vi att tryckförhållandet, uttryckt i dB, var detsamma som effektförhållandet: det var orsaken till faktorn 20 när man definierar dB för tryck. Det är värt att notera att i exemplet med spänningsförstärkning är det osannolikt att förstärkarens effektförstärkning är lika med spänningsförstärkningen, som definieras enligt den konvention som används här. Effekten är proportionell mot kvadraten på spänningen i ett givet motstånd. Ingångs- och utgångsimpedanserna hos förstärkare är dock ofta ganska olika. Till exempel har en buffertförstärkare eller emitterföljare en spänningsförstärkning på ungefär 1, men en stor strömförstärkning).

• Vad är skillnaden, i dB, mellan irradiansen (ljusintensiteten) på jorden (8,3 ljusminuter från solen) och på Uranus (160 ljusminuter)?

  Likt ljudet minskar den isotropa ljusintensiteten som r-2, så intensitetsförhållandet är (160/8.3)2 = 20 log (160/8,3) = 26 dB.

Arbetsmiljö

Olika länder och provinser har uppenbarligen olika lagar om bullerexponering i arbetet, som tillämpas med olika entusiasm. Många av dessa bestämmelser har en gräns för exponering för kontinuerligt buller på 85 dB(A) för ett åttatimmarsskift. För varje ökning med 3 dB halveras den tillåtna exponeringen. Om du arbetar på en nattklubb där förstärkt musik ger 100 dB(A) nära dina öron är den tillåtna exponeringen 15 minuter. Det finns en gräns för impulsljud som skjutvapen eller verktyg som använder explosiva skott. (Det finns många dokument med råd om hur man kan minska bullerexponeringen vid källan (t.ex. sänka musiknivån), mellan källan och örat (t.ex. flytta sig bort från högtalarna på en konsert) och vid örat (t.ex. använda öronproppar eller industriella hörselskydd). Bullerhantering och hörselskydd på arbetsplatsen är den praxis som gäller i delstaten New South Wales i Australien (författarens adress).

Vissa vanliga frågor

• Hur högt är ett flygplan? Ett tåg? En person som sjunger? En hund som skäller? Ett elverktyg? Svaren på denna fråga varierar avsevärt. Det beror i hög grad på hur långt bort du befinner dig, om du är inomhus eller inte, om det finns efterklang, hur stark den specifika källan är och vilket spektrum den har. Att ge värden utan att vara mycket specifik om förhållandena skulle vara något missvisande. Eftersom resten av den här sidan är avsedd att vara tillförlitlig, så långt det är möjligt, vill jag helst inte ge värden här.
• Hur ”adderar man decibel”, det vill säga vilken ljudnivå får man när man adderar nivå a till nivå b? Om källorna är koherenta (vilket vanligtvis innebär att de i slutändan kommer från samma källa) kan det uppstå komplicerade interferenseffekter. I de flesta fall, där källorna är oberoende, kan man addera intensiteterna och sedan konvertera till decibel. Om man får ljudnivåerna i dB(A) är det dock inte så lätt att gå tillbaka till intensitet, och man måste veta något om ljudets spektrum. Om du känner till ljudets fördelning i olika frekvensband kan du använda appleten på den här länken.
• Some of the questions on our FAQ in music acoustics relate to decibels, including
  • Why do the sounds of two musical instruments always reinforce, and never cancel out?
  • How much does one more violin add to the sound level of a section of n violins?
  • Does adding two equal sounds give an increase of 3 or 6 dB? Why?
  • What is the loudest sound?
  • Is there really no sound in space?

Related pages

• Measure your own hearing response
• Adding sound levels from incoherent sources
• What are interference beats and Tartini tones?
• FAQ in music acoustics
• Loudness and spectra: how spectral content and other features are related to loudness
• Formants: what are they? A discussion of the different meanings of this term
• Music acoustics home page
• Physclips: a multi-level, multimedia introduction to mechanics.
• A list of other educational web sites from this author.