Elektromagnetisk strålning
TheoryEdit
Maxwells ekvationerRedigera
James Clerk Maxwell härledde en vågform av de elektriska och magnetiska ekvationerna och avslöjade på så sätt de elektriska och magnetiska fältens vågliknande karaktär och deras symmetri. Eftersom hastigheten hos EM-vågor som förutsades av vågekvationen sammanföll med den uppmätta ljushastigheten, drog Maxwell slutsatsen att ljuset i sig självt är en EM-våg. Maxwells ekvationer bekräftades av Heinrich Hertz genom experiment med radiovågor.
Enligt Maxwells ekvationer är ett rumsligt varierande elektriskt fält alltid förknippat med ett magnetfält som förändras med tiden. På samma sätt är ett rumsligt varierande magnetfält förknippat med specifika förändringar över tiden i det elektriska fältet. I en elektromagnetisk våg åtföljs förändringarna i det elektriska fältet alltid av en våg i det magnetiska fältet i en riktning och vice versa. Detta förhållande mellan de två uppstår utan att någon typ av fält orsakar den andra, utan de uppstår tillsammans på samma sätt som förändringar i tid och rum uppstår tillsammans och är sammankopplade i den speciella relativitetsteorin. I själva verket kan magnetfält betraktas som elektriska fält i en annan referensram, och elektriska fält kan betraktas som magnetfält i en annan referensram, men de har samma betydelse eftersom fysiken är densamma i alla referensramar, så det nära förhållandet mellan rums- och tidsförändringar här är mer än en analogi. Tillsammans bildar dessa fält en utbredd elektromagnetisk våg, som rör sig ut i rymden och aldrig mer behöver interagera med källan. Det avlägsna EM-fält som på detta sätt bildas av en laddnings acceleration bär med sig energi som ”strålar” bort genom rymden, därav termen.
Nära och avlägsna fältRedigera

Maxwells ekvationer fastställde att vissa laddningar och strömmar (”källor”) producerar en lokal typ av elektromagnetiskt fält i närheten av dem som inte har EMR:s beteende. Strömmar producerar direkt ett magnetfält, men det är av en magnetisk dipoltyp som avtar med avståndet från strömmen. På liknande sätt producerar rörliga laddningar som pressas isär i en ledare av en förändrad elektrisk potential (t.ex. i en antenn) ett elektriskt fält av typen elektrisk dipol, men även detta avtar med avståndet. Dessa fält utgör närfältet nära EMR-källan. Inget av dessa beteenden är orsaken till EM-strålning. I stället orsakar de elektromagnetiska fält som endast effektivt överför energi till en mottagare som befinner sig mycket nära källan, t.ex. den magnetiska induktionen i en transformator eller det återkopplingsbeteende som sker nära spolen i en metalldetektor. Typiskt sett har närfält en kraftfull effekt på sina egna källor och orsakar en ökad ”belastning” (minskad elektrisk reaktans) i källan eller sändaren närhelst en mottagare tar energi från det elektromagnetiska fältet. Annars ”sprider” sig dessa fält inte fritt ut i rymden och transporterar sin energi iväg utan avståndsbegränsning, utan oscillerar snarare och returnerar sin energi till sändaren om den inte tas emot av en mottagare.
Det elektromagnetiska fjärrfältet består däremot av strålning som är fri från sändaren i den bemärkelsen att sändaren (till skillnad från vad som är fallet med en elektrisk transformator) kräver samma kraft för att sända dessa förändringar i fälten ut, vare sig signalen omedelbart fångas upp eller inte. Denna avlägsna del av det elektromagnetiska fältet är ”elektromagnetisk strålning” (även kallad fjärrfältet). Fjärrfälten sprider sig (strålar) utan att sändaren kan påverka dem. Detta gör att de är oberoende i den meningen att deras existens och energi, efter att de har lämnat sändaren, är helt oberoende av både sändare och mottagare. På grund av energins bevarande är den mängd energi som passerar genom varje sfärisk yta som dras runt källan densamma. Eftersom en sådan yta har en yta som är proportionell mot kvadraten på dess avstånd från källan, minskar effekttätheten hos EM-strålning alltid med den omvända kvadraten på avståndet från källan; detta kallas den omvända kvadratlagen. Detta står i kontrast till dipoldelar av EM-fältet nära källan (närfältet), som varierar i effekt enligt en omvänt kubisk effektlag, och som således inte transporterar en bevarad energimängd över avstånd, utan i stället avtar med avståndet, med dess energi (som nämnts) som snabbt återvänder till sändaren eller absorberas av en närliggande mottagare (t.ex. en sekundärspole i en transformator).
Fjärrfältet (EMR) är beroende av en annan mekanism för sin framställning än närfältet, och av olika termer i Maxwells ekvationer. Medan den magnetiska delen av närfältet beror på strömmar i källan, beror magnetfältet i EMR endast på den lokala förändringen i det elektriska fältet. På liknande sätt beror det elektriska fältet i närfältet direkt på laddningarna och laddningsseparationen i källan, medan det elektriska fältet i EMR beror på en förändring i det lokala magnetfältet. Båda processerna för att producera elektriska och magnetiska EMR-fält har ett annat avståndsberoende än de elektriska och magnetiska dipolfälten i närfältet. Det är därför som EMR-fältet blir dominerande i kraft ”långt” från källorna. Uttrycket ”långt från källor” avser hur långt från källan (som rör sig med ljusets hastighet) en del av det utåtriktade EM-fältet befinner sig vid den tidpunkt då källans strömmar förändras av den varierande källpotentialen, och källan därför har börjat generera ett utåtriktat EM-fält med en annan fas.
En mer kompakt syn på EMR är att det fjärrfält som utgör EMR i allmänhet är den del av EM-fältet som har färdats tillräckligt långt från källan, så att det har blivit helt bortkopplat från all återkoppling till de laddningar och strömmar som ursprungligen var ansvariga för det. När EM-fältet nu är oberoende av källans laddningar är det, när det rör sig längre bort, endast beroende av accelerationerna hos de laddningar som producerade det. Det har inte längre någon stark koppling till laddningarnas direkta fält eller till laddningarnas (strömmarnas) hastighet.
I Liénard-Wiechert-potentialformuleringen av de elektriska och magnetiska fälten till följd av en enskild partikels rörelse (enligt Maxwells ekvationer) är de termer som är förknippade med partikelns acceleration de termer som är ansvariga för den del av fältet som betraktas som elektromagnetisk strålning. Däremot är den term som är förknippad med partikelns förändrade statiska elektriska fält och den magnetiska term som är resultatet av partikelns enhetliga hastighet, båda förknippade med det elektromagnetiska närfältet och utgör inte EM-strålning.
PropertiesEdit

Elektrodynamik är fysiken kring elektromagnetisk strålning, och elektromagnetism är det fysiska fenomen som är förknippat med teorin om elektrodynamik. Elektriska och magnetiska fält lyder under superpositionsegenskaperna. Således bidrar ett fält som beror på en viss partikel eller ett tidsvarierande elektriskt eller magnetiskt fält till de fält som finns i samma utrymme på grund av andra orsaker. Eftersom de är vektorfält adderas dessutom alla magnetiska och elektriska fältvektorer enligt vektoraddition. Inom optiken kan till exempel två eller flera koherenta ljusvågor interagera och genom konstruktiv eller destruktiv interferens ge en resulterande strålning som avviker från summan av de enskilda ljusvågornas beståndsdelar.
Ljusets elektromagnetiska fält påverkas inte av att det rör sig genom statiska elektriska eller magnetiska fält i ett linjärt medium, t.ex. ett vakuum. I icke-linjära medier, såsom vissa kristaller, kan dock interaktioner uppstå mellan ljus och statiska elektriska och magnetiska fält – dessa interaktioner inkluderar Faraday-effekten och Kerr-effekten.
Vid refraktion ändrar en våg som passerar från ett medium till ett annat med olika densitet sin hastighet och riktning när den kommer in i det nya mediet. Förhållandet mellan mediernas brytningsindex bestämmer graden av brytning och sammanfattas av Snells lag. Ljus med sammansatta våglängder (naturligt solljus) sprids till ett synligt spektrum när det passerar genom ett prisma, på grund av det våglängdsberoende brytningsindexet hos prismamaterialet (dispersion); det vill säga varje komponentvåg inom det sammansatta ljuset böjs olika mycket.
EM-strålning uppvisar både vågegenskaper och partikelegenskaper på samma gång (se våg-partikel-dualitet). Både våg- och partikelegenskaper har bekräftats i många experiment. Vågegenskaperna är tydligare när EM-strålning mäts över relativt stora tidsskalor och över stora avstånd medan partikelegenskaperna är tydligare när man mäter små tidsskalor och avstånd. När till exempel elektromagnetisk strålning absorberas av materia kommer partikelliknande egenskaper att bli tydligare när det genomsnittliga antalet fotoner i kuben av den relevanta våglängden är mycket mindre än 1. Det är inte så svårt att experimentellt observera en ojämn energideposition när ljus absorberas, men detta är i sig självt inte ett bevis på ett ”partikulärt” beteende. Det återspeglar snarare materiens kvantnatur. Att visa att ljuset i sig självt är kvantiserat, inte bara dess interaktion med materia, är en mer subtil angelägenhet.
Vissa experiment visar både våg- och partikelnaturen hos elektromagnetiska vågor, t.ex. självinterferensen hos en enskild foton. När en enskild foton skickas genom en interferometer passerar den genom båda vägarna och interfererar med sig själv, som vågor gör, men upptäcks ändå bara en gång av en fotomultiplikator eller annan känslig detektor.
En kvantteori om interaktionen mellan elektromagnetisk strålning och materia, t.ex. elektroner, beskrivs av teorin om kvantelektrodynamik.
Elektromagnetiska vågor kan polariseras, reflekteras, brytas, böjas, diffrakteras eller interferera med varandra.
Wave modelEdit

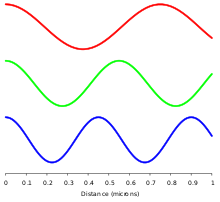
I homogena, isotropa medier är elektromagnetisk strålning en tvärgående våg, vilket innebär att dess svängningar är vinkelräta mot riktningen för energiöverföringen och färden. Den elektriska och magnetiska delen av fältet står i ett fast styrkeförhållande för att uppfylla de två Maxwell-ekvationer som anger hur den ena delen skapas ur den andra. I dissipationsfria (förlustfria) medier är dessa E- och B-fält också i fas, och båda når maxima och minima vid samma punkter i rummet (se illustrationer). En vanlig missuppfattning är att E- och B-fälten i elektromagnetisk strålning är ur fas eftersom en förändring i det ena fältet ger upphov till det andra, vilket skulle ge upphov till en fasskillnad mellan dem som sinusformade funktioner (vilket faktiskt sker vid elektromagnetisk induktion och i närfältet i närheten av antenner). I EM-strålningen i fjärrfältet, som beskrivs av de två källfria Maxwell-ekvationerna för curloperatorn, är dock en mer korrekt beskrivning att en tidsförändring i den ena typen av fält är proportionell mot en rumsförändring i den andra. Dessa derivat kräver att E- och B-fälten i EMR är i fas (se avsnittet om matematik nedan).
En viktig aspekt av ljusets natur är dess frekvens. Frekvensen hos en våg är dess svängningshastighet och mäts i hertz, SI:s enhet för frekvens, där en hertz är lika med en svängning per sekund. Ljus har vanligtvis flera frekvenser som tillsammans bildar den resulterande vågen. Olika frekvenser genomgår olika brytningsvinklar, ett fenomen som kallas dispersion.
En monokromatisk våg (en våg med en enda frekvens) består av på varandra följande dalar och toppar, och avståndet mellan två intilliggande toppar eller dalar kallas våglängd. Vågorna i det elektromagnetiska spektrumet varierar i storlek, från mycket långa radiovågor som är längre än en kontinent till mycket korta gammastrålar som är mindre än atomkärnor. Frekvensen är omvänt proportionell mot våglängden, enligt ekvationen:
v = f λ {\displaystyle \displaystyle v=f\lambda }

där v är vågens hastighet (c i ett vakuum eller mindre i andra medier), f är frekvensen och λ är våglängden. När vågorna passerar gränser mellan olika medier ändras deras hastigheter men deras frekvenser förblir konstanta.
Elektromagnetiska vågor i det fria rummet måste vara lösningar på Maxwells elektromagnetiska vågekvation. Två huvudklasser av lösningar är kända, nämligen plana vågor och sfäriska vågor. De plana vågorna kan ses som gränsfallet för sfäriska vågor vid ett mycket stort (helst oändligt) avstånd från källan. Båda typerna av vågor kan ha en vågform som är en godtycklig tidsfunktion (så länge den är tillräckligt differentierbar för att överensstämma med vågekvationen). Som med alla tidsfunktioner kan denna funktion delas upp med hjälp av Fourieranalys i dess frekvensspektrum eller enskilda sinusformiga komponenter, som var och en innehåller en enda frekvens, amplitud och fas. En sådan komponentvåg sägs vara monokromatisk. En monokromatisk elektromagnetisk våg kan karakteriseras av sin frekvens eller våglängd, sin toppamplitud, sin fas i förhållande till en referensfas, sin utbredningsriktning och sin polarisering.
Interferens är överlagring av två eller flera vågor som resulterar i ett nytt vågmönster. Om fälten har komponenter i samma riktning interfererar de konstruktivt, medan motsatta riktningar orsakar destruktiv interferens. Ett exempel på interferens som orsakas av EMR är elektromagnetisk interferens (EMI) eller som det är mer känt som, radiofrekvensinterferens (RFI). Dessutom kan flera polarisationssignaler kombineras (dvs. interfereras) för att bilda nya polarisationstillstånd, vilket kallas generering av parallella polarisationstillstånd.
Energin i elektromagnetiska vågor kallas ibland för strålningsenergi.
Partikelmodell och kvantteoriRedigera
En anomali uppstod i slutet av 1800-talet som innebar en motsägelse mellan vågteorin om ljus och mätningar av de elektromagnetiska spektrum som sändes ut av termiska strålare som kallas svarta kroppar. Fysikerna kämpade med detta problem utan framgång i många år. Det blev senare känt som den ultravioletta katastrofen. År 1900 utvecklade Max Planck en ny teori om strålning från svarta kroppar som förklarade det observerade spektrumet. Plancks teori byggde på idén att svarta kroppar avger ljus (och annan elektromagnetisk strålning) endast som diskreta buntar eller energipaket. Dessa paket kallades för kvanta. År 1905 föreslog Albert Einstein att ljuskvanta skulle betraktas som verkliga partiklar. Senare fick ljuspartikeln namnet foton, för att motsvara andra partiklar som beskrevs vid den här tiden, t.ex. elektronen och protonen. En foton har en energi, E, som är proportionell mot dess frekvens, f, genom
E = h f = h c λ {\displaystyle E=hf={\frac {hc}{\lambda }}\,\!}

där h är Plancks konstant, λ {\displaystyle \lambda }

är våglängden och c är ljusets hastighet. Detta kallas ibland Planck-Einstein-ekvationen. I kvantteorin (se första kvantisering) är fotonernas energi således direkt proportionell mot EMR-vågens frekvens.
På samma sätt är en fotons rörelsemängd p också proportionell mot frekvensen och omvänt proportionell mot våglängden:
p = E c = h f c = h λ . {\displaystyle p={E \over c}={hf \over c}={h \over \lambda }.}

Källan till Einsteins förslag att ljuset bestod av partiklar (eller kunde agera som partiklar under vissa omständigheter) var en experimentell anomali som inte kunde förklaras av vågteorin: den fotoelektriska effekten, där ljus som träffar en metallyta kastar ut elektroner från ytan, vilket gör att en elektrisk ström flyter över en anlagd spänning. Experimentella mätningar visade att energin hos enskilda utkastade elektroner var proportionell mot ljusets frekvens, snarare än intensitet. Under en viss minimifrekvens, som berodde på den aktuella metallen, flödade ingen ström oavsett intensitet. Dessa observationer tycktes motsäga vågteorin, och i åratal försökte fysikerna förgäves hitta en förklaring. År 1905 förklarade Einstein denna gåta genom att återuppliva partikelteorin om ljuset för att förklara den observerade effekten. På grund av de övervägande bevisen till förmån för vågteorin möttes Einsteins idéer dock till en början med stor skepsis bland etablerade fysiker. Så småningom accepterades Einsteins förklaring när nya partikelliknande beteenden hos ljuset observerades, t.ex. Compton-effekten.
När en foton absorberas av en atom exciteras atomen, vilket förhöjer en elektron till en högre energinivå (en nivå som i genomsnitt befinner sig längre bort från atomkärnan). När en elektron i en exciterad molekyl eller atom sjunker ner till en lägre energinivå avger den en ljusfoton med en frekvens som motsvarar energidifferensen. Eftersom energinivåerna för elektroner i atomer är diskreta avger och absorberar varje grundämne och varje molekyl sina egna karakteristiska frekvenser. Omedelbar fotonemission kallas fluorescens, en typ av fotoluminescens. Ett exempel är synligt ljus som avges av fluorescerande färger som svar på ultraviolett ljus (svartljus). Många andra fluorescerande emissioner är kända i andra spektralband än synligt ljus. Fördröjd emission kallas fosforescens.
Våg-partikeldualitetRedigera
Den moderna teorin som förklarar ljusets natur innefattar begreppet våg-partikeldualitet. Mer allmänt säger teorin att allting har både en partikelnatur och en vågnatur, och olika experiment kan göras för att få fram det ena eller det andra. Partikelnaturen är lättare att urskilja med hjälp av ett föremål med stor massa. Ett djärvt förslag av Louis de Broglie 1924 ledde till att forskarsamhället insåg att även materia (t.ex. elektroner) uppvisar våg-partikel-dualitet.
Våg- och partikeleffekter av elektromagnetisk strålningRedigera
Våg- och partikeleffekter förklarar tillsammans helt och hållet EM-strålningens emissions- och absorptionsspektra. Materiesammansättningen i det medium som ljuset färdas genom bestämmer karaktären på absorptions- och emissionsspektrumet. Dessa band motsvarar de tillåtna energinivåerna i atomerna. Mörka band i absorptionsspektrumet beror på atomer i ett mellanliggande medium mellan källan och observatören. Atomerna absorberar vissa frekvenser av ljuset mellan sändaren och detektorn/ögat och sänder sedan ut dem i alla riktningar. Ett mörkt band visas för detektorn på grund av den strålning som sprids ut från strålen. Exempelvis beror mörka band i det ljus som sänds ut av en avlägsen stjärna på atomerna i stjärnans atmosfär. Ett liknande fenomen inträffar för emission, vilket ses när en emitterande gas glöder på grund av att atomerna exciteras av någon mekanism, inklusive värme. När elektronerna sjunker ner till lägre energinivåer emitteras ett spektrum som representerar hoppen mellan elektronernas energinivåer, men linjer ses eftersom emissionen återigen sker endast vid vissa energinivåer efter excitationen. Ett exempel är emissionsspektrumet från nebulosor. Elektroner som rör sig snabbt accelereras kraftigast när de möter ett kraftområde, så de är ansvariga för att producera en stor del av den elektromagnetiska strålning av högsta frekvens som observeras i naturen.
Dessa fenomen kan vara till hjälp vid olika kemiska bestämningar för sammansättningen av gaser som belyses bakifrån (absorptionsspektra) och för glödande gaser (emissionsspektra). Spektroskopi (till exempel) bestämmer vilka kemiska element som ingår i en viss stjärna. Spektroskopi används också för att bestämma avståndet till en stjärna, med hjälp av rödförskjutningen.
UtbredningshastighetRedigera
När någon tråd (eller annat ledande föremål, till exempel en antenn) leder växelström, fortplantas elektromagnetisk strålning med samma frekvens som strömmen. I många sådana situationer är det möjligt att identifiera ett elektriskt dipolmoment som uppstår genom separation av laddningar på grund av den spännande elektriska potentialen, och detta dipolmoment oscillerar i tiden när laddningarna rör sig fram och tillbaka. Denna svängning vid en given frekvens ger upphov till förändrade elektriska och magnetiska fält, som sedan sätter den elektromagnetiska strålningen i rörelse.
På kvantnivå produceras elektromagnetisk strålning när en laddad partikels vågpaket svänger eller på annat sätt accelereras. Laddade partiklar i ett stationärt tillstånd rör sig inte, men en superposition av sådana tillstånd kan resultera i ett övergångstillstånd som har ett elektriskt dipolmoment som oscillerar i tiden. Detta oscillerande dipolmoment är ansvarigt för fenomenet strålningsövergång mellan kvanttillstånd hos en laddad partikel. Sådana tillstånd förekommer (till exempel) i atomer när fotoner strålar när atomen övergår från ett stationärt tillstånd till ett annat.
Som våg kännetecknas ljuset av en hastighet (ljusets hastighet), en våglängd och en frekvens. Som partiklar är ljus en ström av fotoner. Var och en har en energi som är relaterad till vågens frekvens enligt Plancks relation E = hf, där E är fotonens energi, h är Plancks konstant, 6,626 × 10-34 J-s, och f är vågens frekvens.
En regel följs oavsett omständigheterna: EM-strålning i ett vakuum färdas med ljusets hastighet i förhållande till observatören, oavsett observatörens hastighet. (Denna observation ledde till Einsteins utveckling av den speciella relativitetsteorin.) I ett medium (annat än vakuum) beaktas hastighetsfaktor eller brytningsindex, beroende på frekvens och tillämpning. Båda dessa är förhållandet mellan hastigheten i ett medium och hastigheten i vakuum.
Särskild relativitetsteoriRedigera
I slutet av 1800-talet kunde olika experimentella anomalier inte förklaras med den enkla vågteorin. En av dessa anomalier gällde en kontrovers om ljusets hastighet. Ljusets och andra EMR:s hastighet som förutsades av Maxwells ekvationer uppträdde inte om inte ekvationerna ändrades på ett sätt som först föreslogs av FitzGerald och Lorentz (se den speciella relativitetsteorins historia), annars skulle den hastigheten bero på observatörens hastighet i förhållande till ”mediet” (kallat luminiferisk eter) som förmodades ”bära” den elektromagnetiska vågen (på ett sätt som är analogt med det sätt på vilket luft bär ljudvågor). Experiment misslyckades med att hitta någon observatörseffekt. År 1905 föreslog Einstein att rum och tid tycktes vara hastighetsförändringsbara enheter för ljusets utbredning och alla andra processer och lagar. Dessa förändringar förklarade att ljusets hastighet och all elektromagnetisk strålning är konstant från alla observatörers synvinkel – även de som befinner sig i relativ rörelse.