Framtidsvärde av växande livränta

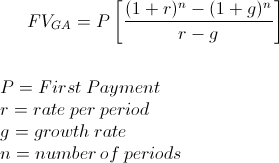
Formeln för framtidsvärdet av en växande livränta används för att beräkna det framtida beloppet av en serie kassaflöden, eller utbetalningar, som växer med en proportionell hastighet. En växande annuitet kan ibland kallas för en ökande annuitet.

Exempel på FV av växande annuitet

Ett exempel på formeln för det framtida värdet av en växande annuitet är en person som får lön varannan vecka och som bestämmer sig för att spara en av sina extra löner per år. En av hennes nettolöner uppgår till 2 000 dollar det första året och hon räknar med att få en höjning på 5 % av sin nettolön varje år. I det här exemplet kommer vi att använda 5 % av hennes nettolön och inte ta med skatter och andra justeringar för att hålla alla andra saker konstanta. På ett konto med en avkastning på 3 % per år vill hon beräkna sitt sparsaldo efter 5 år.

Växthastigheten i det här exemplet skulle vara 5 % ökning per år, det ursprungliga kassaflödet eller betalningen skulle vara 2 000 dollar, antalet perioder skulle vara 5 år och räntan per period skulle vara 3 %. Att använda dessa variabler i formeln för det framtida värdet av växande annuitet skulle visa

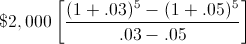
Efter att ha löst denna ekvation skulle beloppet efter det 5:e kassaflödet vara 11 700,75 dollar.

Hur härleds FV för växande annuitet?

Det framtida värdet av en växande annuitetsformel kan hittas genom att först titta på följande formel för nuvärdet av en växande annuitetsformel

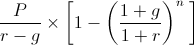
Nuvärdet kan omvandlas till ett framtida värde genom att multiplicera nuvärdet gånger (1+r)n. By multiplying the 2nd portion of the PV of growing annuity formula above by (1+r)n, the formula would show as

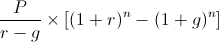
From here, the formula above is the same as the formula shown at the top of the page after factoring out the initial payment, P.

Return to Top

• Formulas related to FV of Growing Annuity
• PV of Growing Annuity
• FV of Annuity
• FV of Annuity Due
• Growing Annuity Payment (FV)