Interpolationstyper – fördelar och nackdelar
Interpolationsmetoder
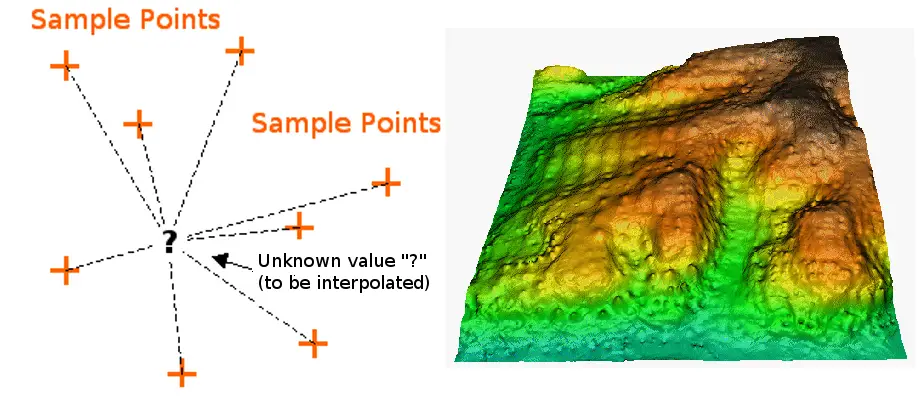
Interpolation är en process där man använder punkter med kända värden eller provpunkter för att uppskatta värden i andra okända punkter. Den kan användas för att förutsäga okända värden för alla geografiska punktdata, t.ex. höjd, nederbörd, kemiska koncentrationer, bullernivåer och så vidare.
De tillgängliga interpolationsmetoderna listas nedan.
Inverse Distance Weighted (IDW)
Interpolatorn med omvänd avståndsviktning utgår från att varje inmatningspunkt har ett lokalt inflytande som avtar med avståndet. Den viktar de punkter som ligger närmare bearbetningscellen högre än de som ligger längre bort. Ett specificerat antal punkter eller alla punkter inom en specificerad radie kan användas för att bestämma utgångsvärdet för varje plats. Användning av denna metod förutsätter att variabeln som kartläggs minskar i inflytande med avståndet från dess provtagningsplats.
IDW Interpolation; med tillstånd: QGIS
Algoritmen IDW (Inverse Distance Weighting) är i själva verket en interpolator för glidande medelvärde som vanligtvis tillämpas på mycket varierande data. För vissa datatyper är det möjligt att återvända till insamlingsplatsen och registrera ett nytt värde som statistiskt sett skiljer sig från den ursprungliga avläsningen men som ligger inom den allmänna trenden för området.
Den interpolerade ytan, som uppskattas med hjälp av en teknik med rörligt medelvärde, är mindre än det lokala maximivärdet och större än det lokala minimivärdet.

IDW Interpolated Surface; Med vänlig hälsning:ESRI
IDW-interpolering implementerar uttryckligen antagandet att saker som ligger nära varandra är mer lika än saker som ligger längre ifrån varandra. För att förutsäga ett värde för en icke mätt plats använder IDW de uppmätta värden som omger platsen för förutsägelsen. De uppmätta värden som ligger närmast den förutspådda platsen kommer att ha större inflytande på det förutspådda värdet än de som ligger längre bort. IDW utgår alltså från att varje uppmätt punkt har ett lokalt inflytande som minskar med avståndet. IDW-funktionen bör användas när mängden punkter är tillräckligt tät för att fånga den lokala ytvariation som behövs för analysen. IDW bestämmer cellvärden med hjälp av en linjärt viktad kombination av provpunkter. Den viktar de punkter som ligger närmare prediktionsplatsen större än de som ligger längre bort, därav namnet inverse distance weighted.
IDW-tekniken beräknar ett värde för varje rutnätsnod genom att undersöka omgivande datapunkter som ligger inom en användardefinierad sökradie. Vissa eller alla datapunkter kan användas i interpoleringsprocessen. Nodvärdet beräknas genom att medelvärdet av den viktade summan av alla punkter beräknas. Datapunkter som ligger successivt längre bort från noden påverkar det beräknade värdet mycket mindre än de som ligger närmare noden.
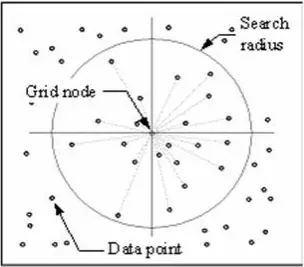
En radie genereras runt varje nätnod från vilken datapunkter väljs ut för att användas i beräkningen. Options to control the use of IDW include power, search radius, fixed search radius, variable search radius and barrier.
Note: The optimal power (p) value is determined by minimizing the root mean square prediction error (RMSPE).
Advantages
- Can estimate extreme changes in terrain such as: Cliffs, Fault Lines.
- Dense evenly space points are well interpolated (flat areas with cliffs).
- Can increase or decrease amount of sample points to influence cell values.
Disadvantages
- Cannot estimate above maximum or below minimum values.
- Not very good for peaks or mountainous areas.
Natural Neighbour Inverse Distance Weighted (NNIDW)
Natural neighbor interpolation has many positive features, can be used for both interpolation and extrapolation, and generally works well with clustered scatter points. Den grundläggande ekvation som används vid interpolering av naturliga grannar är identisk med den ekvation som används vid IDW-interpolering. Denna metod kan effektivt hantera stora datamängder med inmatade punkter. Vid användning av Natural Neighbor-metoden definierar lokala koordinater hur mycket inflytande en spridnings punkt kommer att ha på utdatacellerna.
The Natural Neighbour-metoden är en geometrisk estimeringsteknik som använder sig av naturliga grannskapsregioner som genereras runt varje punkt i datamängden.
Likt IDW är den här interpolationsmetoden en metod för interpolation av vägda medelvärden. Men i stället för att hitta en interpolerad punkts värde med hjälp av alla ingångspunkter viktade efter deras avstånd, skapar Natural Neighbors interpolation en Delauney-triangulering av ingångspunkterna och väljer de närmaste noderna som bildar ett konvext skrov runt interpolationspunkten, och viktar sedan deras värden efter proportionell yta. Den här metoden är lämpligast när datapunkterna är fördelade med ojämn täthet. Det är en bra interpolationsteknik för allmänna ändamål och har fördelen att man inte behöver ange parametrar som radie, antal grannar eller vikter.

Natural IDW: Med tillstånd: ESRI
Denna teknik är utformad för att hedra lokala minimi- och maximivärden i punktfilen och kan ställas in för att begränsa överskridanden av lokala höga värden och underskridanden av lokala låga värden. Metoden gör det därmed möjligt att skapa noggranna ytmodeller från datamängder som är mycket sparsamt fördelade eller mycket linjära i den rumsliga fördelningen.
Fördelar
- Hanterar ett stort antal provpunkter på ett effektivt sätt.
Spline
Spline uppskattar värden med hjälp av en matematisk funktion som minimerar den totala ytkrökningen, vilket resulterar i en slät yta som passerar exakt genom inmatningspunkterna.

Spline::: ESRI
Spline: Courtesy: ESRI
Konceptuellt sett är det analogt med att böja en gummiplåt så att den passerar genom kända punkter samtidigt som den totala krökningen av ytan minimeras. Den anpassar en matematisk funktion till ett specificerat antal närmsta inmatningspunkter samtidigt som den passerar genom provpunkterna. Denna metod är bäst för mjukt varierande ytor, t.ex. höjdskillnader, grundvattennivåer eller föroreningskoncentrationer.
Spline-metoden för interpolation uppskattar okända värden genom att böja en yta genom kända värden.
Det finns två splinemetoder: regulariserad och spline.
En regulariserad metod skapar en jämn, gradvis föränderlig yta med värden som kan ligga utanför provdataområdet. Den innehåller första derivatan (lutning), andra derivatan (förändringshastighet i lutningen) och tredje derivatan (förändringshastighet i andra derivatan) i sina minimeringsberäkningar.
En yta som skapats med Spline-interpolation passerar genom varje provpunkt och kan överskrida värdeområdet för provpunktsgruppen.
Och även om en Tension spline endast använder första och andra derivatan, ingår fler punkter i Spline-beräkningarna, vilket vanligtvis skapar jämnare ytor men ökar beräkningstiden.
Denna metod drar en yta över de förvärvade punkterna vilket resulterar i en sträckt effekt. Spline använder krökta linjer (metoden curvilinear Lines) för att beräkna cellvärden.
Välja en vikt för Spline-interpolationer
Regulariserad spline: Ju högre vikt, desto jämnare yta. Vikter mellan 0 och 5 är lämpliga. Typiska värden är 0, 0,001, 0,01, 0,1 och 0,5.
Tensionspline: Ju högre vikt, desto grövre är ytan och desto mer överensstämmer värdena med intervallet för provdata. Viktvärdena måste vara större än eller lika med noll. Typical values are 0, 1, 5, and 10.
Advantages
- Useful for estimating above maximum and below minimum points.
- Creates a smooth surface effect.
Disadvantages
- Cliffs and fault lines are not well presented because of the smoothing effect.
- When the sample points are close together and have extreme differences in value, Spline interpolation doesn’t work as well. This is because Spline uses slope calculations (change over distance) to figure out the shape of the flexible rubber sheet.
Kriging
Kriging is a geostatistical interpolation technique that considers both the distance and the degree of variation between known data points when estimating values in unknown areas. A kriged estimate is a weighted linear combination of the known sample values around the point to be estimated.
Krigingförfarande som genererar en uppskattad yta från en spridd uppsättning punkter med z-värden. Kriging utgår från att avståndet eller riktningen mellan provpunkterna återspeglar en rumslig korrelation som kan användas för att förklara variationen i ytan. Kriging-verktyget anpassar en matematisk funktion till ett visst antal punkter, eller alla punkter inom en viss radie, för att bestämma utgångsvärdet för varje plats. Kriging är en process i flera steg; den omfattar utforskande statistisk analys av data, variogrammodellering, skapande av ytan och (valfritt) utforskning av en variansyta. Kriging är lämpligast när man vet att det finns ett rumsligt korrelerat avstånd eller en riktningsförskjutning i data. Det används ofta inom markvetenskap och geologi.
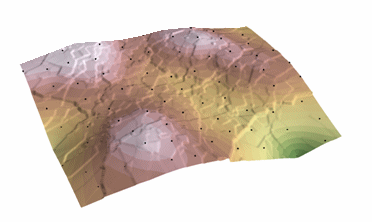
Kriging: Courtesy: ESRI
The predicted values are derived from the measure of relationship in samples using sophisticated weighted average technique. It uses a search radius that can be fixed or variable. The generated cell values can exceed value range of samples, and the surface does not pass through samples.
The Kriging Formula
Kriging is similar to IDW in that it weights the surrounding measured values to derive a prediction for an unmeasured location. The general formula for both interpolators is formed as a weighted sum of the data:
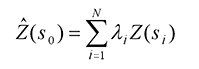
- where:
Z(si) = the measured value at the ith location
λi = an unknown weight for the measured value at the ith location
s0 = the prediction location
N = the number of measured values
In IDW, the weight, λi, depends solely on the distance to the prediction location. Men med krigingmetoden baseras vikterna inte bara på avståndet mellan de uppmätta punkterna och prediktionsplatsen utan även på det övergripande rumsliga arrangemanget av de uppmätta punkterna. För att använda det rumsliga arrangemanget i vikterna måste den rumsliga autokorrelationen kvantifieras. I vanlig kriging beror alltså vikten λi på en anpassad modell till de uppmätta punkterna, avståndet till förutsägelseplatsen och de rumsliga förhållandena mellan de uppmätta värdena runt förutsägelseplatsen. I följande avsnitt diskuteras hur den allmänna krigingformeln används för att skapa en karta över prediktionsytan och en karta över prediktionernas noggrannhet.
Typer av Kriging
Ordinär Kriging
Ordinär kriging utgår från modellen
Z(s) = µ + ε(s),
där µ är en okänd konstant. En av de viktigaste frågorna när det gäller vanlig kriging är om antagandet om ett konstant medelvärde är rimligt. Sometimes there are good scientific reasons to reject this assumption. However, as a simple prediction method, it has remarkable flexibility.
Ordinary kriging can use either semivariograms or covariances, use transformations and remove trends, and allow for measurement error.
Simple Kriging
Simple kriging assumes the model
Z(s) = µ + ε(s),
where µ is a known constant.
Simple kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Universal Kriging
Universal kriging assumes the model
Z(s) = µ(s) + ε(s),
where µ(s) is some deterministic function.
Universal kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Indikatorkriging
Indikatorkriging utgår från modellen
I(s) = µ + ε(s),
där µ är en okänd konstant och I(s) är en binär variabel. Skapandet av binära data kan ske genom användning av ett tröskelvärde för kontinuerliga data, eller så kan det vara så att de observerade data är 0 eller 1. Du kan till exempel ha ett urval som består av information om huruvida en punkt är skogsbiotop eller ej, där den binära variabeln anger klasstillhörighet. Vid användning av binära variabler går indikatorkrigning till på samma sätt som vanlig krigning.
Indikatorkrigning kan använda antingen semivariogram eller kovarianser.
Probability Kriging
Probability kriging utgår från modellen
I(s) = I(Z(s) > ct) = µ1 + ε1(s)Z(s) = µ2 + ε2(s),
där µ1 och µ2 är okända konstanter och I(s) är en binär variabel som skapats genom att använda en tröskelindikator, I(Z(s) > ct). Observera att det nu finns två typer av slumpmässiga fel, ε1(s) och ε2(s), så det finns autokorrelation för var och en av dem och korskorrelation mellan dem. Sannolikhetskriging strävar efter att göra samma sak som indikatorkriging, men använder cokriging i ett försök att göra ett bättre jobb.
Probability kriging kan använda antingen semivariogram eller kovarianser, korskovarianser och transformationer, men kan inte ta hänsyn till mätfel.
style=”display:inline-block;width:468px;height:60px” data-ad-client=”ca-pub-7134201556760050″ data-ad-slot=”9271753327″>
Disjunktiv Kriging
Disjunktiv Kriging utgår från att modell
f(Z(s)) = µ1 + ε(s),
där µ1 är en okänd konstant och f(Z(s)) är en godtycklig funktion av Z(s). Observera att man kan skriva f(Z(s)) = I(Z(s) > ct), så indikatorkrigning är ett specialfall av disjunktiv krigning. I Geostatistical Analyst kan du förutsäga antingen själva värdet eller en indikator med disjunktiv kriging.
Generellt sett försöker disjunktiv kriging göra mer än vanlig kriging. Även om belöningen kan vara större, är kostnaderna också större. Disjunctive kriging requires the bivariate normality assumption and approximations to the functions fi(Z(si)); the assumptions are difficult to verify, and the solutions are mathematically and computationally complicated.
Disjunctive kriging can use either semivariograms or covariances and transformations, but it cannot allow for measurement error.
Advantages
- Directional influences can be accounted for: Soil Erosion, Siltation Flow, Lava Flow and Winds.
- Exceeds the minimum and maximum point values
Disadvantages
- Does not pass through any of the point values and causes interpolated values to be higher or lower then real values.
**** För att få en djupare inblick i det matematiska tillvägagångssättet för Kriging, klicka på Kriging a Interpolation Method.
PointInterp
En metod som liknar IDW, men PointInterp-funktionen ger mer kontroll över provtagningsområdet. Hur ett visst prov påverkar det interpolerade värdet för rutnätscellen beror på om provpunkten ligger i cellens grannskap och hur långt från den interpolerade cellen den är belägen. Punkter utanför grannskapet har inget inflytande.

PointInterp; med tillstånd: ESRI
Det viktade värdet av punkterna i grannskapet beräknas med hjälp av en omvänd avståndsviktad interpolation eller omvänd exponentiell avståndsinterpolation. Denna metod interpolerar ett raster med hjälp av punktfunktioner men tillåter olika typer av grannskap. Grannskap kan ha former som cirklar, rektanglar, oregelbundna polygoner, annulus eller kilar.
Trend
Trend är en statistisk metod som hittar den yta som passar provpunkterna med hjälp av en regressionsanpassning med minsta kvadrat. Den anpassar en polynomisk ekvation till hela ytan. Detta resulterar i en yta som minimerar ytvariansen i förhållande till ingångsvärdena. Ytan konstrueras så att för varje inmatningspunkt blir summan av skillnaderna mellan de faktiska värdena och de uppskattade värdena (dvs. variansen) så liten som möjligt.

Trend; Courtsey:ESRI
Det är en inexakt interpolator, och den resulterande ytan går sällan genom ingångspunkterna. Den här metoden upptäcker dock trender i provdata och liknar naturliga fenomen som vanligtvis varierar jämnt.
Fördel
- Trendytor är bra för att identifiera grovskaliga mönster i data; den interpolerade ytan passerar sällan genom provpunkterna.
Topo to Raster
Genom att interpolera höjdvärden för ett raster inför Topo to Raster-metoden begränsningar som säkerställer en hydrologiskt korrekt digital höjdmodell som innehåller en sammanhängande dräneringsstruktur och representerar åsar och bäckar på ett korrekt sätt från inmatade konturdata. Metoden använder en iterativ interpolationsteknik med finita skillnader som optimerar den lokala interpolationens beräkningseffektivitet utan att förlora den globala interpolationens ytkontinuitet. Den har utformats särskilt för att arbeta intelligent med konturinmatningar.
Nedan visas ett exempel på en yta som interpolerats från höjdpunkter, konturlinjer, vattendragslinjer och sjöpolygoner med hjälp av interpolering från topografi till raster.
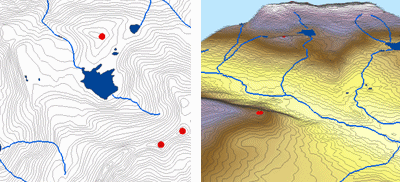
Topo to raster; med tillstånd: ESRI
Topo to Raster är ett specialiserat verktyg för att skapa hydrologiskt korrekta rasterytor från vektordata om terrängkomponenter, t.ex. höjdpunkter, konturlinjer, vattendragslinjer, polygoner av sjöar, sänkor och polygoner som avgränsar studieområden.
Täthet
Täthetsverktyg (tillgängliga i ArcGIS) producerar en yta som representerar hur mycket eller hur många av något som finns per ytenhet. Densitetsverktyget är användbart för att skapa täthetsytor för att representera fördelningen av en djurpopulation utifrån en uppsättning observationer, eller graden av urbanisering av ett område baserat på vägarnas täthet.

Density Raster; Courtest: ERSI
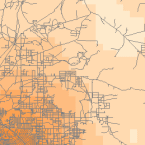
Density and Roads; Courtesy: ESRI
There are density tools for point and line features in ArcGIS.
Related Topics
- What is Interpolation ?
- Classification of Interpolation Techniques.
- Choosing the Right Interpolation Method