Kilogram: Mass och Plancks konstant
Max Planck (1858-1947) hade ursprungligen ingen aning om hur allmänt tillämpbar hans begrepp ”kvantum” skulle bli, inklusive dess roll för att mäta massa. Han tänkte sig det i samband med ett envist problem inom 1800-talets fysik: En ledande teori på den tiden förutspådde på ett nonsensmässigt sätt att vissa föremål skulle utstråla en oändlig mängd kraft när de släppte ut elektromagnetisk strålning med höga frekvenser (och därmed korta våglängder, det vill säga mot den ultravioletta delen av spektrumet i diagrammet nedan) – en situation som blev känd som ”ultraviolettkatastrofen”.”
Planck postulerade att elektromagnetisk energi vid en given frekvens endast kunde avges i diskreta mängder, eller kvanta, vars energi är proportionell mot h, numera känd som Planckkonstanten.
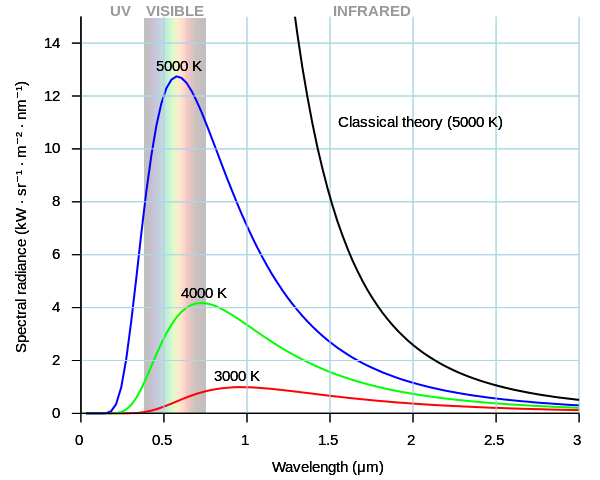
Bilden ovan visar vad den klassiska teorin (den svarta linjen) förutspådde jämfört med de blå, gröna och röda linjerna som härleds från Plancks formulering, vilka stämmer utmärkt överens med fysiska mätningar.
Massa, Planck och Einstein
Hur kan SI:s kilogramenhet – förkroppsligad i en enda metallklump som gjöts på 1800-talet – omdefinieras i termer av en invariant i naturen och skalas upp eller ner på ett bekvämt, exakt och upprepande sätt?

Efter årtionden av debatt har den internationella mätningsvetenskapen valt att besvara den frågan genom att använda Plancks konstant.
För många observatörer är kopplingen mellan massa i storleksordningen en liter vatten och en konstant som härrör från kvantmekanikens allra tidigaste dagar kanske inte omedelbart uppenbar. Det vetenskapliga sammanhanget för detta samband antyds av ett djupt underliggande förhållande mellan två av fysikens mest berömda formuleringar.
Den ena är Einsteins berömda E =mc2, där E är energi, m är massa och c är ljusets hastighet. Det andra uttrycket, som är mindre känt för allmänheten men grundläggande för den moderna vetenskapen, är E = hν, det första ”kvantuttrycket” i historien, som Max Planck formulerade år 1900. Här är E energi, ν är frekvens (ν är inte ett ”v” utan i stället den grekiska bokstaven nu) och h är det som nu kallas Planckkonstanten.
Einsteins nist-ekvation visar att massa kan förstås och till och med kvantifieras i termer av energi. Plancks nist-ekvation visar att energi i sin tur kan beräknas i termer av frekvensen ν hos en entitet som till exempel en foton (en ljuspartikel), eller alternativt, med vissa matematiska utbyten, en massa – gånger en multipel av h. Multiplen måste vara ett positivt heltal – till exempel 1, 2 eller 3. Det är helhetsaspekten som gör förhållandet ”kvantiserat” – materia frigör energi i diskreta bitar, så kallade ”kvanta”, som kan föreställas som enskilda energipaket eller energibuntar.
Om man tar de två nist-ekvationerna tillsammans får man en kontraintuitiv men enormt värdefull insikt: Planck använde först denna beteckning för att beskriva det försvinnande lilla energiinnehållet i enskilda fotoner som avges av atomer i varma föremål. Värdet på h är ungefär 0,6 triljondelar av en triljondel av en miljarddel av en joule-sekund. Joule är SI-enheten för energi.
I praktiken blev experiment som kopplar massa till h med extraordinär precision möjliga i slutet av 1900-talet som ett resultat av två separata upptäckter som ledde till två olika fysikaliska konstanter relaterade till spänning respektive motstånd.
Dessa är Josephsonkonstanten (KJ = 2e/h) och von Klitzingkonstanten (RK = h/e2).
Josephsonkonstanten är relaterad till växelströms-Josephson-effekten. Denna uppstår när en spänning som läggs över en supraledande förbindelse skapar en elektrisk växelström med en frekvens som är proportionell mot spänningen. Frekvensen kan mätas mer exakt än någon annan kvantitet (något som regelbundet utnyttjas av atomklockor, som låser sig vid mikrovågsfrekvenser eller optiska frekvenser av elektromagnetisk strålning som avges av atomer). KJ ger ett extremt exakt sätt att mäta spänningen.
Von Klitzing-konstanten RK beskriver hur elektriskt motstånd existerar i diskreta, kvantiserade värden (i stället för kontinuerliga) i vissa typer av fysiska system. På grund av sin utomordentligt höga precision används RK över hela världen som standard för elektrisk resistans.
Balans eller sfärer?
Under 1990-talet intensifierades debatten om möjliga sätt att omdefiniera kilogrammet som skulle göra det möjligt att avskaffa artefaktstandarden. Två huvudsakliga tankesätt framträdde. Den ena skulle definiera kilogrammet i termer av massan av en kiselatom genom att räkna antalet atomer i en 1-kilosfär av ultrarent kisel-28 (den vanligaste isotopen av kisel, som innehåller totalt 28 protoner och neutroner).
Den andra metoden förespråkades bland annat av NIST-forskarna Peter Mohr och Barry Taylor. År 1999 föreslog de i ett brev som publicerades i tidskriften Metrologia att tilldela Planckkonstanten ett fast värde som grund för en ny kilogramdefinition. Mohr och Taylor undersökte användningen av en Kibble-balans, en komplex anordning som mäter massan exakt med hjälp av elektriska mätningar.
Namnet efter den brittiske fysikern Bryan Kibble, utvecklades Kibblebalansen för första gången 1975 vid det brittiska National Physical Laboratory (NPL). En byggdes kort därefter vid NIST. På 1980-talet var forskare vid NPL och NIST mycket engagerade i att använda Kibblebalanser för att bestämma värdet av h.
Mohr och Taylor resonerade att om en Kibblebalans kunde använda en exakt definierad massa för att mäta det okända värdet av h, så skulle processen kunna vara omvänd: Genom att ställa in ett exakt fastställt värde av h skulle samma system kunna användas för att mäta en okänd massa.
Idén, som kom att kallas det ”elektriska” eller ”elektroniska” kilogrammet, diskuterades flitigt och godkändes slutligen i princip av den internationella allmänna konferensen om mått och vikt (CGPM), med några få krav. Minst tre experiment måste ge mätningar med en relativ standardosäkerhet på högst 50 delar per miljard, där minst en av dessa mätningar har en osäkerhet på högst 20 delar per miljard. Alla dessa värden måste stämma överens inom en statistisk konfidensnivå på 95 procent.
I mitten av 2017 antog det internationella forskarsamhället utmaningen och lyckades uppfylla dessa krav.

Uppåt ett halvt dussin Kibble-vikter är i drift runt om i världen. NIST:s slutliga h-mätning som lämnades in för det omdefinierade SI hade en osäkerhet på 13 delar på en miljard. En annan Kibblebalansmätning, från National Research Council (NRC) i Kanada, hade en osäkerhet på endast 9,1 delar per miljard. (NRC hade fått en Kibble-balans från NPL 2009.) Två andra Kibble-balansmätningar, inklusive en från LNE (Laboratoire National de Métrologie et d’Essais i Frankrike), hade de nödvändiga noggrannhetsnivåerna. Fyra mätningar från Avogadros ”kiselkula” uppfyllde också de internationella kraven, varav tre från den multinationella IAC (International Avogadro Coordination) och en från NMIJ (National Metrology Institute of Japan).
När mätningarna analyserades av CODATA:s arbetsgrupp för grundläggande konstanter gav de ett slutvärde för h på 6,62607015 × 10-34 kg⋅m2/s, med en osäkerhet på 10 delar per miljard. När SI omdefinierades fastställdes detta som det exakta värdet av Plancks konstant, som i sin tur definierar andra SI-enheter, bland annat kilogrammet.