Marginalfördelning

Sannolikhetsfördelningar > Marginalfördelning

Vad är en marginalfördelning?

Klipp på videon eller läs artikeln nedan:

Den tekniska definitionen kan vara lite tankspridd att titta på:

Definition av en marginalfördelning = Om X och Y är diskreta slumpmässiga variabler och f (x,y) är värdet av
deras gemensamma sannolikhetsfördelning vid (x,y), är funktionerna som ges av:
g(x) = Σy f (x,y) och h(y) = Σx f (x,y) är marginalfördelningarna för X respektive Y.

Om du är duktig på ekvationer är det förmodligen allt du behöver veta. Det berättar hur man hittar en marginalfördelning. Men om den formeln ger dig huvudvärk (vilket den gör för de flesta!) kan du använda en frekvensfördelningstabell för att hitta en marginalfördelning.

En marginalfördelning har fått sitt namn eftersom den visas i marginalerna i en sannolikhetsfördelningstabell.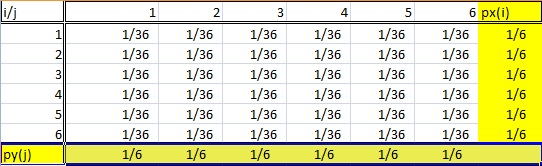

Självklart är det inte riktigt så enkelt som det. Man kan inte bara titta på vilken gammal frekvensfördelningstabell som helst och säga att den sista kolumnen (eller raden) är en ”marginalfördelning”. Marginalfördelningar följer ett par regler:

• Fördelningen måste vara från bivariata data. Bivariat är bara ett annat sätt att säga ”två variabler”, som X och Y. I tabellen ovan kommer de slumpmässiga variablerna i och j från två tärningskast.
• En marginalfördelning är när du bara är intresserad av en av de slumpmässiga variablerna . Med andra ord, antingen X eller Y. Om du tittar på sannolikhetstabellen ovan, listas summesannolikheterna för en variabel på den nedre raden och de andra summesannolikheterna i den högra kolumnen. Den här tabellen har alltså två marginalfördelningar.

Skillnaden mellan marginalfördelning och villkorlig fördelning.

En villkorlig fördelning är när vi bara är intresserade av en viss delpopulation av hela vår datamängd. I exemplet med tärningskastningen kan detta vara att ”kasta en tvåa” eller ”kasta en sexa”. Bilden nedan visar två markerade delpopulationer (och därmed två betingade fördelningar).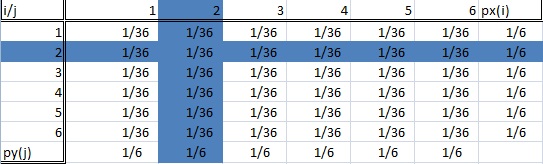

Hur man beräknar marginalfördelningens sannolikhet

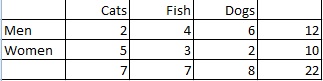
Exempel på fråga: Beräkna marginalfördelningen av preferenser för husdjur bland män och kvinnor:
Lösning:
Steg 1: Räkna det totala antalet personer. I det här fallet anges summan i den högra kolumnen (22 personer).
Steg 2: Räkna antalet personer som föredrar varje typ av husdjur och omvandla sedan förhållandet till en sannolikhet:
Personer som föredrar katter: 7/22 = 0,32
Personer som föredrar fisk: 7/22 = 0,32
Personer som föredrar hundar: 8/22 = 0,36
Tip: Du kan kontrollera ditt svar genom att se till att sannolikheterna summerar till 1.

Exempelfråga 2 (ömsesidigt uteslutande händelser): Om P(A) = 0,20, P(b) = 0,70 och båda händelserna är ömsesidigt uteslutande, hitta P(B’∩A), P(B’∩A’) och P(B∩A’).
Om du inte är bekant med denna notation betyder P(A’) ”inte A”, eller komplementet. P(B’∩A) betyder ”skärningspunkten mellan inte B och A”).

Svar:
Du skulle kunna räkna ut sannolikheterna individuellt, men det är mycket lättare att räkna ut dem med hjälp av en tabell.

Steg 1: Fyll i en frekvenstabell med den givna informationen. Den totala sannolikheten måste vara lika med 1, så du kan också lägga till den till marginalerna(totalerna). Enkel addition/algebra fyller ut marginalerna. Till exempel, på den nedersta raden 0,70 + x = 1,00 så Den marginella summan för B’ måste vara 0,30.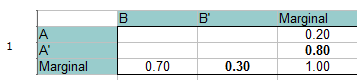

Steg 2: Lägg till 0 för skärningspunkten mellan A och B, högst upp till vänster i tabellen. Det kan du göra eftersom A och B utesluter varandra och inte kan inträffa tillsammans.

Steg 3: Fyll i resten av luckorna med hjälp av enkel addition/algebra.

Läsning från tabellen (titta på skärningspunkterna mellan de två angivna sannolikheterna):
P(B’∩A) = 0,20
P(B’∩A’) = 0,10
P(B∩A’) = 0,70.

Exempelfråga 3 (oberoende händelser): Om P(A) = 0,20, P(b) = 0,70 och båda händelserna är oberoende, hitta P(B’∩A), P(B’∩A’) och P(B∩A’).

Svar: Den här gången är A och B oberoende av varandra, så sannolikheten för att båda inträffar samtidigt är 0,14 (P(A)*P(B) = 0,20 * 0,70 = 0,14). Detta värde placeras i det övre vänstra fältet (skärningspunkten mellan A och B). Fyll i resten av tabellen på exakt samma sätt som i stegen ovan.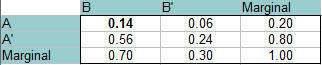

Läs svaren från tabellen (från skärningspunkterna mellan de två sannolikheterna):
P(B’∩A): 0.06
P(B’∩A’): 0,24
P(B∩A’): 0,56.

Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, s. 536 och 571, 2002.
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Lindström, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education

——————————————————————————

Behövs hjälp med en läxa eller en provfråga? Med Chegg Study kan du få steg-för-steg-lösningar på dina frågor från en expert inom området. Dina första 30 minuter med en Chegg-handledare är gratis!