Solving the Königsberg Bridge Problem
This proof is accessible to ANYONE — no mathematics knowledge required! (perfect for if you are a bit bored and in isolation, like me right now!)
The Königsberg bridge problem shows the beauty of mathematics to transform the impossible to the obvious. It also gives an insight into the mind of the genius Leonhard Euler.

Stating the problem
Have a look at the map above.
It’s a diagram of the rivers and bridges of Königsberg. The areas A, B, C and D are bits of land, joined by the bridges, but otherwise cut off from each other by water.
A map of the city is below. Du kan titta på båda diagrammen – båda fångar den viktigaste informationen: vilka landområden som är förbundna med vilka andra landområden och med hur många broar.
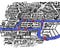
På fackspråk representerar vi detta som ett diagram. Landklumparna är hörnpunkterna och broarna är kanterna. Men det är inte viktigt.
Problemet är om det är möjligt att hitta en rutt som går över varje bro exakt en gång. Det betyder att vi under vår promenad i staden vill att vår rutt ska gå över varje bro, men den kan inte gå över den två gånger, eller tre gånger… I princip är vägen ogiltig om du befinner dig på samma bro som du var tidigare. Om du avslutar din promenad och det finns en bro som du inte gick över så var din väg ogiltig.
Lösningen
Konsultera varje klump mark. Varje bro är kopplad till två landklumpar (det är så broar fungerar). Varje landklump råkar ha ett udda antal broar kopplade till sig.
Nu kan vi fundera på hur en giltig vandring skulle se ut.
När du går på din vandring antecknar du i ett anteckningsblock varje gång du befinner dig i en viss landklump. Om du till exempel börjar i den sydligaste delen av staden gör du en anteckning om det (ta ett foto, köp en souvenir…) och om du befinner dig där igen ökar du räkningen för den södra sektorn till två.
För varje klump mark finns det två fall
(1) detta är en stadsdel som vi varken börjar vår vandring i eller avslutar vår vandring där
(2) detta är en stadsdel som vi antingen börjar vår vandring i eller avslutar vår vandring i eller både och
Det är tydligt att det finns högst två stadsdelar av den andra typen. Vi kan inte börja på två ställen samtidigt, och vi kan inte heller avsluta på två ställen samtidigt.
Då det finns fyra delar av staden betyder det att det finns minst två delar av staden, i vår vandring, som vi varken avslutar eller börjar på. Låt oss välja en av dem.
När vi går in i den sektorn använder vi en bro, och när vi lämnar den använder vi en annan. Men varje sektor har ett udda antal broar knutna till sig! Det är en motsägelse. För att se varför, kom ihåg att varje sektor antingen har 3 broar, eller så har den 5 broar knutna till sig.
Om vi är i sektorn en gång kan vi bara använda två av dess broar. Om vi är i den två gånger skulle vi använda fyra av dess broar (eller få slut på broar om den bara hade tre broar). Om vi är i den tre gånger skulle vi behöva 6 broar, vilket vi inte kan ha. Kravet att vi både ska gå in i och ut ur en sektor av staden som inte är vår start- eller slutpunkt motsäger alltså det faktum att antalet anslutande broar är udda för varje sektor.